Chapter 7: Nonlinear Valuation#
rs_utility.py#
from quantecon import compute_fixed_point
from quantecon.markov import tauchen
import numpy as np
from numba import njit
from collections import namedtuple
# NamedTuple Model
Model = namedtuple("Model", ("β", "θ", "ρ", "σ", "r", "x_vals", "P"))
def create_rs_utility_model(
n=180, # size of state space
β=0.95, # time discount factor
ρ=0.96, # correlation coef in AR(1)
σ=0.1, # volatility
θ=-1.0): # risk aversion
mc = tauchen(n, ρ, σ, 0, 10) # n_std = 10
x_vals, P = mc.state_values, mc.P
r = x_vals # special case u(c(x)) = x
return Model(β=β, θ=θ, ρ=ρ, σ=σ, r=r, x_vals=x_vals, P=P)
@njit
def K(v, model):
β, θ, ρ, σ, r, x_vals, P = model
return r + (β/θ) * np.log(np.dot(P, (np.exp(θ*v))))
def compute_rs_utility(model):
β, θ, ρ, σ, r, x_vals, P = model
v_init = np.zeros(len(x_vals))
v_star = compute_fixed_point(lambda v: K(v, model), v_init,
error_tol=1e-10, max_iter=1000, print_skip=25)
return v_star
# Plots
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams.update({"text.usetex": True, "font.size": 14})
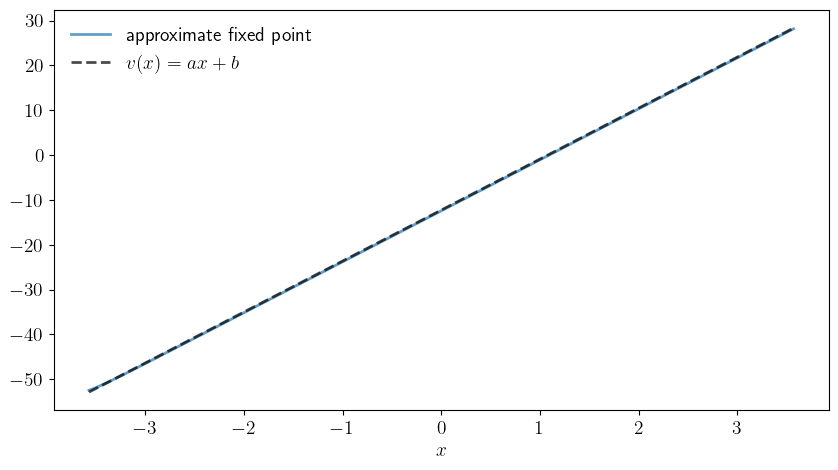
def plot_v(savefig=False,
figname="./figures/rs_utility_1.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
model = create_rs_utility_model()
β, θ, ρ, σ, r, x_vals, P = model
a = 1/(1 - (ρ*β))
b = (β /(1 - β)) * (θ/2) * (a*σ)**2
v_star = compute_rs_utility(model)
v_star_a = a * x_vals + b
ax.plot(x_vals, v_star, linewidth=2, alpha=0.7,
label="approximate fixed point")
ax.plot(x_vals, v_star_a, "k--", linewidth=2, alpha=0.7,
label=r"$v(x)=ax + b$")
ax.set_xlabel(r"$x$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
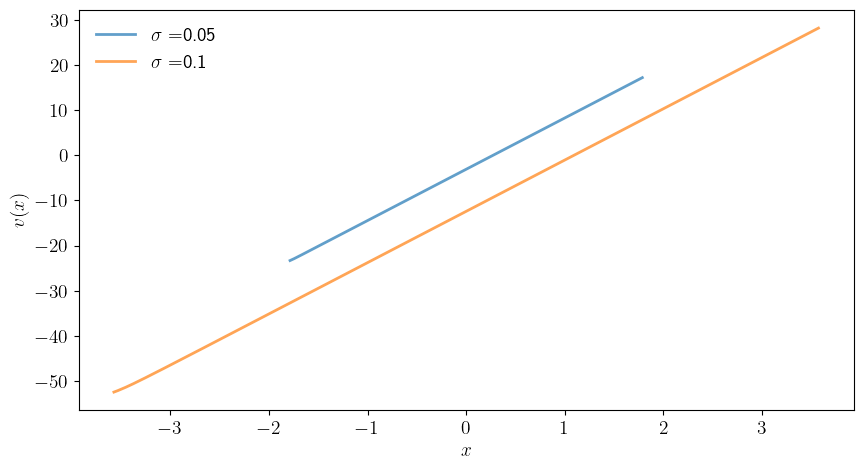
def plot_multiple_v(savefig=False,
figname="./figures/rs_utility_2.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
σ_vals = 0.05, 0.1
for σ in σ_vals:
model = create_rs_utility_model(σ=σ)
β, θ, ρ, σ, r, x_vals, P = model
v_star = compute_rs_utility(model)
ax.plot(x_vals, v_star, linewidth=2, alpha=0.7,
label=r"$\sigma=$" + f"{σ}")
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$v(x)$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
plot_v()
Iteration Distance Elapsed (seconds)
---------------------------------------------
25 6.552e-01 1.088e+00
50 1.657e-01 1.091e+00
75 4.489e-02 1.094e+00
100 1.237e-02 1.096e+00
125 3.424e-03 1.099e+00
150 9.492e-04 1.102e+00
175 2.632e-04 1.105e+00
200 7.302e-05 1.107e+00
225 2.025e-05 1.110e+00
250 5.618e-06 1.112e+00
275 1.558e-06 1.115e+00
300 4.323e-07 1.117e+00
325 1.199e-07 1.120e+00
350 3.326e-08 1.121e+00
375 9.227e-09 1.122e+00
400 2.559e-09 1.123e+00
425 7.100e-10 1.124e+00
450 1.969e-10 1.124e+00
464 9.604e-11 1.125e+00
Converged in 464 steps
plot_multiple_v()
Iteration Distance Elapsed (seconds)
---------------------------------------------
25 2.636e-01 3.805e-03
50 5.190e-02 6.443e-03
75 1.235e-02 9.102e-03
100 3.222e-03 1.179e-02
125 8.734e-04 1.441e-02
150 2.402e-04 1.689e-02
175 6.643e-05 1.942e-02
200 1.841e-05 2.208e-02
225 5.104e-06 2.442e-02
250 1.416e-06 2.565e-02
275 3.927e-07 2.649e-02
300 1.089e-07 2.738e-02
325 3.021e-08 2.820e-02
350 8.380e-09 2.901e-02
375 2.325e-09 2.984e-02
400 6.448e-10 3.066e-02
425 1.789e-10 3.149e-02
437 9.666e-11 3.189e-02
Converged in 437 steps
Iteration Distance Elapsed (seconds)
---------------------------------------------
25 6.552e-01 8.059e-04
50 1.657e-01 1.500e-03
75 4.489e-02 2.193e-03
100 1.237e-02 2.891e-03
125 3.424e-03 3.561e-03
150 9.492e-04 4.224e-03
175 2.632e-04 4.875e-03
200 7.302e-05 5.519e-03
225 2.025e-05 6.165e-03
250 5.618e-06 6.840e-03
275 1.558e-06 7.821e-03
300 4.323e-07 8.487e-03
325 1.199e-07 9.132e-03
350 3.326e-08 9.774e-03
375 9.227e-09 1.042e-02
400 2.559e-09 1.108e-02
425 7.100e-10 1.173e-02
450 1.969e-10 1.237e-02
464 9.604e-11 1.273e-02
Converged in 464 steps
ez_utility.py#
"""
Epstein--Zin utility: solving the recursion for a given consumption
path.
"""
from quantecon import compute_fixed_point
from quantecon.markov import tauchen
import numpy as np
from numba import njit
from collections import namedtuple
# NamedTuple Model
Model = namedtuple("Model", ("β", "ρ", "σ", "α", "γ", "c", "x_vals", "P"))
def create_ez_utility_model(
n=200, # size of state space
ρ=0.96, # correlation coef in AR(1)
σ=0.1, # volatility
β=0.99, # time discount factor
α=0.75, # EIS parameter
γ=-2.0): # risk aversion parameter
mc = tauchen(n, ρ, σ, 0, 5)
x_vals, P = mc.state_values, mc.P
c = np.exp(x_vals)
return Model(β=β, ρ=ρ, σ=σ, α=α, γ=γ, c=c, x_vals=x_vals, P=P)
@njit
def K(v, model):
β, ρ, σ, α, γ, c, x_vals, P = model
R = np.dot(P, v**γ)**(1/γ)
return ((1 - β) * c**α + β * R**α)**(1/α)
def compute_ez_utility(model):
v_init = np.ones(len(model.x_vals))
v_star = compute_fixed_point(lambda v: K(v, model), v_init,
error_tol=1e-6, max_iter=1000, print_skip=100)
return v_star
# Plots
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams.update({"text.usetex": True, "font.size": 14})
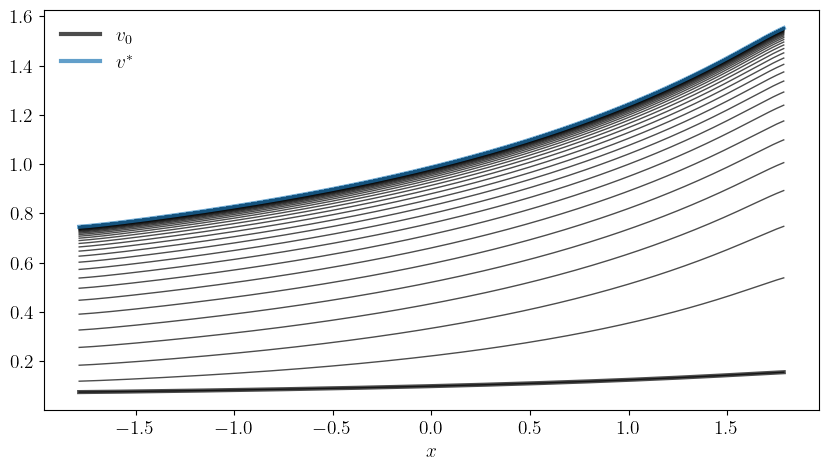
def plot_convergence(savefig=False,
num_iter=100,
figname="./figures/ez_utility_c.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
model = create_ez_utility_model()
β, ρ, σ, α, γ, c, x_vals, P = model
v_star = compute_ez_utility(model)
v = 0.1 * v_star
ax.plot(x_vals, v, "k-", linewidth=3, alpha=0.7, label=r"$v_0$")
greys = [str(g) for g in np.linspace(0.0, 0.4, num_iter)]
greys.reverse()
for g in greys:
ax.plot(x_vals, v, "k-", linewidth=1, alpha=0.7)
for t in range(20):
v = K(v, model)
v_star = compute_ez_utility(model)
ax.plot(x_vals, v_star, linewidth=3, alpha=0.7, label=r"$v^*$")
ax.set_xlabel(r"$x$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
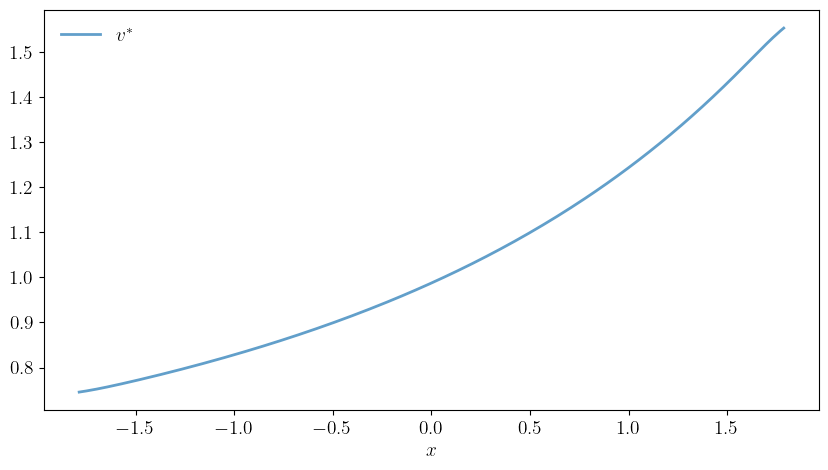
def plot_v(savefig=False,
figname="./figures/ez_utility_1.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
model = create_ez_utility_model()
β, ρ, σ, α, γ, c, x_vals, P = model
v_star = compute_ez_utility(model)
ax.plot(x_vals, v_star, linewidth=2, alpha=0.7, label=r"$v^*$")
ax.set_xlabel(r"$x$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
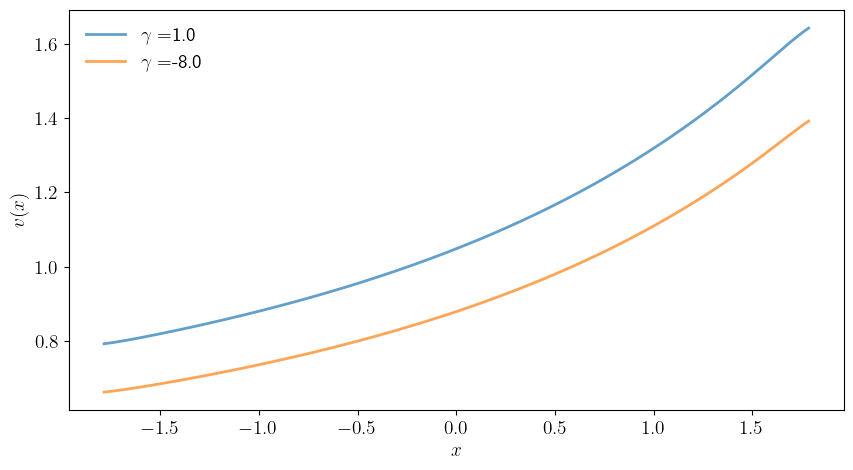
def vary_gamma(gamma_vals=[1.0, -8.0],
savefig=False,
figname="./figures/ez_utility_2.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
for γ in gamma_vals:
model = create_ez_utility_model(γ=γ)
β, ρ, σ, α, γ, c, x_vals, P = model
v_star = compute_ez_utility(model)
ax.plot(x_vals, v_star, linewidth=2, alpha=0.7, label=r"$\gamma=$" + f"{γ}")
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$v(x)$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
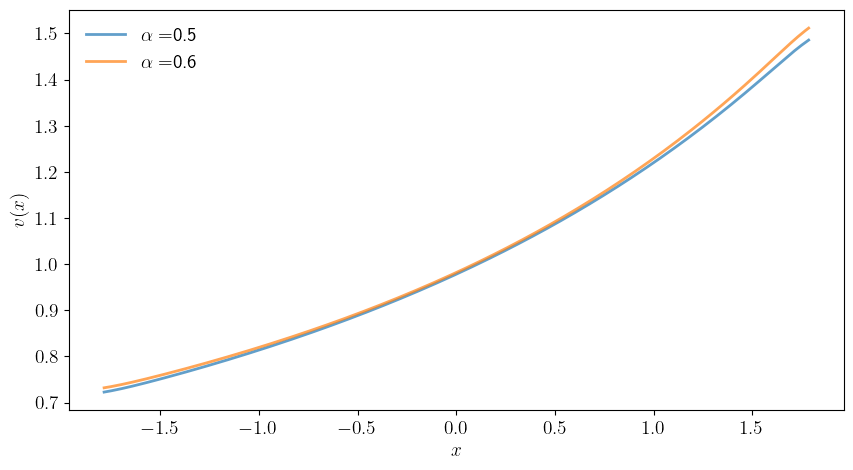
def vary_alpha(alpha_vals=[0.5, 0.6],
savefig=False,
figname="./figures/ez_utility_3.pdf"):
fig, ax = plt.subplots(figsize=(10, 5.2))
for α in alpha_vals:
model = create_ez_utility_model(α=α)
β, ρ, σ, α, γ, c, x_vals, P = model
v_star = compute_ez_utility(model)
ax.plot(x_vals, v_star, linewidth=2, alpha=0.7, label=r"$\alpha=$"+f"{α}")
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$v(x)$")
ax.legend(frameon=False, loc="upper left")
if savefig:
fig.savefig(figname)
plot_convergence()
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 1.790e-04 4.081e-01
200 4.296e-05 4.211e-01
300 1.660e-05 4.354e-01
400 6.320e-06 4.452e-01
500 2.406e-06 4.506e-01
591 9.992e-07 4.553e-01
Converged in 591 steps
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 1.790e-04 4.147e-03
200 4.296e-05 1.016e-02
300 1.660e-05 1.422e-02
400 6.320e-06 1.830e-02
500 2.406e-06 2.235e-02
591 9.992e-07 2.601e-02
Converged in 591 steps
plot_v()
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 1.790e-04 1.405e-02
200 4.296e-05 2.629e-02
300 1.660e-05 3.849e-02
400 6.320e-06 5.100e-02
500 2.406e-06 6.324e-02
591 9.992e-07 7.454e-02
Converged in 591 steps
vary_gamma()
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 3.700e-04 1.603e-02
200 8.647e-05 2.859e-02
300 3.125e-05 4.082e-02
400 1.140e-05 5.296e-02
500 4.156e-06 6.573e-02
600 1.516e-06 7.824e-02
642 9.921e-07 8.340e-02
Converged in 642 steps
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 6.104e-04 1.328e-02
200 2.817e-04 2.545e-02
300 1.147e-04 3.792e-02
400 4.681e-05 5.001e-02
500 1.912e-05 6.219e-02
600 7.814e-06 6.804e-02
700 3.194e-06 7.272e-02
800 1.306e-06 7.728e-02
830 9.985e-07 7.865e-02
Converged in 830 steps
vary_alpha()
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 1.989e-04 1.328e-02
200 6.184e-05 2.549e-02
300 2.346e-05 3.805e-02
400 8.796e-06 5.074e-02
500 3.299e-06 6.303e-02
600 1.237e-06 7.570e-02
622 9.972e-07 7.856e-02
Converged in 622 steps
Iteration Distance Elapsed (seconds)
---------------------------------------------
100 1.917e-04 1.200e-02
200 5.408e-05 1.746e-02
300 2.066e-05 2.154e-02
400 7.793e-06 2.556e-02
500 2.940e-06 2.959e-02
600 1.109e-06 3.371e-02
611 9.962e-07 3.417e-02
Converged in 611 steps