15. 自适应预期下的货币主义价格水平理论

15.1. 引言

本讲座可以被看作是 货币主义价格水平理论 的续篇或前传。

我们将运用线性代数来探讨另一种”货币主义”或”财政”价格水平理论。

与 货币主义价格水平理论 中的模型类似，本模型认为，当政府实施持续性的财政赤字并通过印钞来弥补时，会推高价格水平并导致持续通货膨胀。

不同于 货币主义价格水平理论 中的”完全预见”或”理性预期”版本，本讲座介绍的是菲利普·凯根 [Cagan, 1956] 用于研究恶性通货膨胀动态的”自适应预期”版本。

该模型包含以下几个要素：

• 一个实际货币需求函数，表明所需实际货币余额的对数与公众预期通胀率呈负相关

• 一个自适应预期模型，描述公众如何根据过去的实际通胀率调整其通胀预期

• 一个货币供需均衡条件

• 一个外生的货币供应增长率序列

我们的模型与凯根的原始模型非常接近。

与 现值 和 消费平滑 讲座一样，我们只需要用到矩阵乘法和矩阵求逆这些基本的线性代数运算。

为了便于使用线性矩阵代数作为主要分析工具，我们将研究模型的有限视界版本。

15.2. 模型结构

令：

• \( m_t \) 为名义货币余额的对数

• \(\mu_t = m_{t+1} - m_t \) 为名义货币余额的增长率

• \(p_t \) 为价格水平的对数

• \(\pi_t = p_{t+1} - p_t \) 为 \(t\) 到 \( t+1\) 期间的通胀率

• \(\pi_t^*\) 为公众对 \(t\) 到 \(t+1\) 期间通胀率的预期

• \(T\) 为时间跨度 – 即模型确定 \(p_t\) 的最后一期

• \(\pi_0^*\) 为公众对第0期到第1期通胀率的初始预期

实际货币余额 \(\exp\left(\frac{m_t^d}{p_t}\right)\) 的需求由以下凯根需求函数决定：

(15.1)\[ m_t^d - p_t = -\alpha \pi_t^* \: , \: \alpha > 0 ; \quad t = 0, 1, \ldots, T . \]

该方程表明，实际货币余额需求与预期通胀率成反比。

将方程 (15.1) 中的货币需求对数 \(m_t^d\) 设为等于货币供给对数 \(m_t\)，并求解价格水平对数 \(p_t\)，得到：

(15.2)\[ p_t = m_t + \alpha \pi_t^* \]

对方程 (15.2) 求时间差分，得到：

(15.3)\[ \pi_t = \mu_t + \alpha \pi_{t+1}^* - \alpha \pi_t^* \]

我们假设预期通胀率 \(\pi_t^*\) 遵循弗里德曼-凯根的自适应预期机制：

(15.4)\[ \pi_{t+1}^* = \lambda \pi_t^* + (1 -\lambda) \pi_t \]

模型的外生输入包括初始条件 \(m_0, \pi_0^*\) 和货币增长序列 \(\mu = \{\mu_t\}_{t=0}^T\)。

模型的内生输出是序列 \(\pi = \{\pi_t\}_{t=0}^T\) 和 \(p = \{p_t\}_{t=0}^T\)，它们是外生输入的函数。

我们将通过研究模型输出如何随输入变化而变化来进行一些思想实验。

15.3. 关键方程的矩阵表示

首先，我们将方程 (15.4) 中的自适应预期模型写成 \(t=0, \ldots, T\) 的矩阵形式：

\[ \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \cr -\lambda & 1 & 0 & \cdots & 0 & 0 \cr 0 & - \lambda & 1 & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \cr 0 & 0 & 0 & \cdots & -\lambda & 1 \end{bmatrix} \begin{bmatrix} \pi_0^* \cr \pi_1^* \cr \pi_2^* \cr \vdots \cr \pi_{T+1}^* \end{bmatrix} = (1-\lambda) \begin{bmatrix} 0 & 0 & 0 & \cdots & 0 \cr 1 & 0 & 0 & \cdots & 0 \cr 0 & 1 & 0 & \cdots & 0 \cr \vdots &\vdots & \vdots & \cdots & \vdots \cr 0 & 0 & 0 & \cdots & 1 \end{bmatrix} \begin{bmatrix}\pi_0 \cr \pi_1 \cr \pi_2 \cr \vdots \cr \pi_T \end{bmatrix} + \begin{bmatrix} \pi_0^* \cr 0 \cr 0 \cr \vdots \cr 0 \end{bmatrix} \]

让我们将上述方程简洁地写成矩阵形式：

(15.5)\[ A \pi^* = (1-\lambda) B \pi + \pi_0^* \]

其中 \(A\) 是一个 \((T+2) \times (T+2)\) 矩阵，\(B\) 是一个 \((T+2)\times (T+1)\) 矩阵，\(\pi^*\)、\(\pi\) 和 \(\pi_0^*\) 是相应的向量。这些矩阵和向量的具体形式可以通过比较上述两个等式得到。

现在，让我们将方程 (15.3) 表示为矩阵形式

\[ \begin{bmatrix} \pi_0 \cr \pi_1 \cr \pi_1 \cr \vdots \cr \pi_T \end{bmatrix} = \begin{bmatrix} \mu_0 \cr \mu_1 \cr \mu_2 \cr \vdots \cr \mu_T \end{bmatrix} + \begin{bmatrix} - \alpha & \alpha & 0 & \cdots & 0 & 0 \cr 0 & -\alpha & \alpha & \cdots & 0 & 0 \cr 0 & 0 & -\alpha & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \cdots & \alpha & 0 \cr 0 & 0 & 0 & \cdots & -\alpha & \alpha \end{bmatrix} \begin{bmatrix} \pi_0^* \cr \pi_1^* \cr \pi_2^* \cr \vdots \cr \pi_{T+1}^* \end{bmatrix} \]

让我们用向量和矩阵简洁地表示上述方程系统:

(15.6)\[ \pi = \mu + C \pi^* \]

其中 \(C\) 是一个 \((T+1) \times (T+2)\) 矩阵,其形式可以从前面的方程系统中看出。

15.4. 求解模型

现在我们有了求解 \(\pi\) 作为 \(\mu, \pi_0, \pi_0^*\) 函数所需的所有要素。

将方程 (15.5) 和 (15.6) 结合:

\[ \begin{aligned} A \pi^* & = (1-\lambda) B \pi + \pi_0^* \cr & = (1-\lambda) B \left[ \mu + C \pi^* \right] + \pi_0^* \end{aligned} \]

整理得到:

\[ \left[ A - (1-\lambda) B C \right] \pi^* = (1-\lambda) B \mu+ \pi_0^* \]

求解 \(\pi^*\):

(15.7)\[ \pi^* = \left[ A - (1-\lambda) B C \right]^{-1} \left[ (1-\lambda) B \mu+ \pi_0^* \right] \]

有了 \(\pi^*\),我们就可以从方程 (15.6) 求出 \(\pi\):

\[ \pi = \mu + C \pi^* \]

这样我们就解出了模型的两个关键内生变量序列:预期通货膨胀率 \(\pi^*\) 和实际通货膨胀率 \(\pi\)。

有了这些,我们就可以从方程 (15.2) 计算出价格水平对数序列 \(p\)。

让我们来看看具体步骤。

首先,已知 \(\mu\),我们可以计算货币供应 \(m\)。

注意到方程

\[ m_{t+1} = m_t + \mu_t , \quad t = 0, 1, \ldots, T \]

可以写成矩阵形式:

(15.8)\[ \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \cr -1 & 1 & 0 & \cdots & 0 & 0 \cr 0 & -1 & 1 & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & 0 & 0 \cr 0 & 0 & 0 & \cdots & 1 & 0 \cr 0 & 0 & 0 & \cdots & -1 & 1 \end{bmatrix} \begin{bmatrix} m_1 \cr m_2 \cr m_3 \cr \vdots \cr m_T \cr m_{T+1} \end{bmatrix} = \begin{bmatrix} \mu_0 \cr \mu_1 \cr \mu_2 \cr \vdots \cr \mu_{T-1} \cr \mu_T \end{bmatrix} + \begin{bmatrix} m_0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr 0 \end{bmatrix} \]

将方程 (15.8) 的两边都乘以左侧矩阵的逆矩阵，我们得到

(15.9)\[ m_t = m_0 + \sum_{s=0}^{t-1} \mu_s, \quad t =1, \ldots, T+1 \]

方程 (15.9) 表明，时间 \(t\) 的货币供应对数等于初始货币供应对数 \(m_0\) 加上 \(0\) 到 \(t\) 时间之间货币增长率的累积。

然后我们可以从方程 (15.2) 计算每个 \(t\) 的 \(p_t\)。

我们可以为 \(p\) 写一个紧凑的公式 $\( p = m + \alpha \hat \pi^* \)$

其中

\[ \hat \pi^* = \begin{bmatrix} \pi_0^* \cr \pi_1^* \cr \pi_2^* \cr \vdots \cr \pi_{T}^* \end{bmatrix}, \]

这是去掉最后一个元素的 \(\pi^*\)。

15.5. 预期与实际通货膨胀的差异

在这个适应性预期模型中，人们的通货膨胀预期通常会与实际通货膨胀率不同。具体来说，我们的计算将显示：

\[ \hat \pi^* \neq \pi, \]

也就是说，对于任意时期 \(t\)，预期通货膨胀率与实际通货膨胀率不相等：

(15.10)\[ \pi_t^* \neq \pi_t, \quad t = 0, 1, \ldots , T \]

这种预期误差是适应性预期模型的一个典型特征。在这类模型中，人们根据过去的经验逐步调整他们的预期，如方程 (15.4) 所示。

这与我们在 价格水平的货币主义理论 中研究的”完美预见”或”理性预期”版本形成对比。在那个版本中，人们能够完全准确地预测通货膨胀。

让我们通过一些数值实验来探索这个适应性预期版本的具体表现。首先，我们需要导入必要的Python模块：

import numpy as np
from collections import namedtuple
import matplotlib.pyplot as plt

Cagan_Adaptive = namedtuple("Cagan_Adaptive", 
                        ["α", "m0", "Eπ0", "T", "λ"])

def create_cagan_model(α, m0, Eπ0, T, λ):
    return Cagan_Adaptive(α, m0, Eπ0, T, λ)

这里我们定义这些参数。

# 参数
T = 80
T1 = 60
α = 5
λ = 0.9
m0 = 1

μ0 = 0.5
μ_star = 0

md = create_cagan_model(α=α, m0=m0, Eπ0=μ0, T=T, λ=λ)

我们用以下的函数来求解模型并且绘制这些变量。

def solve(model, μ_seq):
    "在求解有限视界的凯根模型"
    
    model_params = model.α, model.m0, model.Eπ0, model.T, model.λ
    α, m0, Eπ0, T, λ = model_params
    
    A = np.eye(T+2, T+2) - λ*np.eye(T+2, T+2, k=-1)
    B = np.eye(T+2, T+1, k=-1)
    C = -α*np.eye(T+1, T+2) + α*np.eye(T+1, T+2, k=1)
    Eπ0_seq = np.append(Eπ0, np.zeros(T+1))

    # Eπ_seq 的长度为 T+2
    Eπ_seq = np.linalg.inv(A - (1-λ)*B @ C) @ ((1-λ) * B @ μ_seq + Eπ0_seq)

    # π_seq 的长度为 T+1
    π_seq = μ_seq + C @ Eπ_seq

    D = np.eye(T+1, T+1) - np.eye(T+1, T+1, k=-1)
    m0_seq = np.append(m0, np.zeros(T))

    # m_seq 的长度为 T+2
    m_seq = np.linalg.inv(D) @ (μ_seq + m0_seq)
    m_seq = np.append(m0, m_seq)

    # p_seq 的长度为 T+2
    p_seq = m_seq + α * Eπ_seq

    return π_seq, Eπ_seq, m_seq, p_seq

def solve_and_plot(model, μ_seq):
    
    π_seq, Eπ_seq, m_seq, p_seq = solve(model, μ_seq)
    
    T_seq = range(model.T+2)
    
    fig, ax = plt.subplots(5, 1, figsize=[5, 12], dpi=200)
    ax[0].plot(T_seq[:-1], μ_seq)
    ax[1].plot(T_seq[:-1], π_seq, label=r'$\pi_t$')
    ax[1].plot(T_seq, Eπ_seq, label=r'$\pi^{*}_{t}$')
    ax[2].plot(T_seq, m_seq - p_seq)
    ax[3].plot(T_seq, m_seq)
    ax[4].plot(T_seq, p_seq)
    
    y_labs = [r'$\mu$', r'$\pi$', r'$m - p$', r'$m$', r'$p$']

    for i in range(5):
        ax[i].set_xlabel(r'$t$')
        ax[i].set_ylabel(y_labs[i])

    ax[1].legend()
    plt.tight_layout()
    plt.show()
    
    return π_seq, Eπ_seq, m_seq, p_seq

15.6. 稳定性的条件

在构建我们的示例时，我们假设 \((\lambda, \alpha)\) 满足

(15.11)\[ \Bigl| \frac{\lambda-\alpha(1-\lambda)}{1-\alpha(1-\lambda)} \Bigr| < 1 \]

这个条件的来源是以下一系列推导：

\[\begin{split} \begin{aligned} \pi_{t}&=\mu_{t}+\alpha\pi_{t+1}^{*}-\alpha\pi_{t}^{*}\\\pi_{t+1}^{*}&=\lambda\pi_{t}^{*}+(1-\lambda)\pi_{t}\\\pi_{t}&=\frac{\mu_{t}}{1-\alpha(1-\lambda)}-\frac{\alpha(1-\lambda)}{1-\alpha(1-\lambda)}\pi_{t}^{*}\\\implies\pi_{t}^{*}&=\frac{1}{\alpha(1-\lambda)}\mu_{t}-\frac{1-\alpha(1-\lambda)}{\alpha(1-\lambda)}\pi_{t}\\\pi_{t+1}&=\frac{\mu_{t+1}}{1-\alpha(1-\lambda)}-\frac{\alpha(1-\lambda)}{1-\alpha(1-\lambda)}\left(\lambda\pi_{t}^{*}+(1-\lambda)\pi_{t}\right)\\&=\frac{\mu_{t+1}}{1-\alpha(1-\lambda)}-\frac{\lambda}{1-\alpha(1-\lambda)}\mu_{t}+\frac{\lambda-\alpha(1-\lambda)}{1-\alpha(1-\lambda)}\pi_{t} \end{aligned} \end{split}\]

通过确保 \(\pi_t\) 的系数绝对值小于1，条件(15.11)保证了由我们推导过程最后一行描述的 \(\{\pi_t\}\) 动态的稳定性。

读者可以尝试探索当条件(15.11)不满足时会发生什么情况。

print(np.abs((λ - α*(1-λ))/(1 - α*(1-λ))))

0.8

print(λ - α*(1-λ))

0.40000000000000013

现在我们来看一些实验。

15.6.1. 实验1

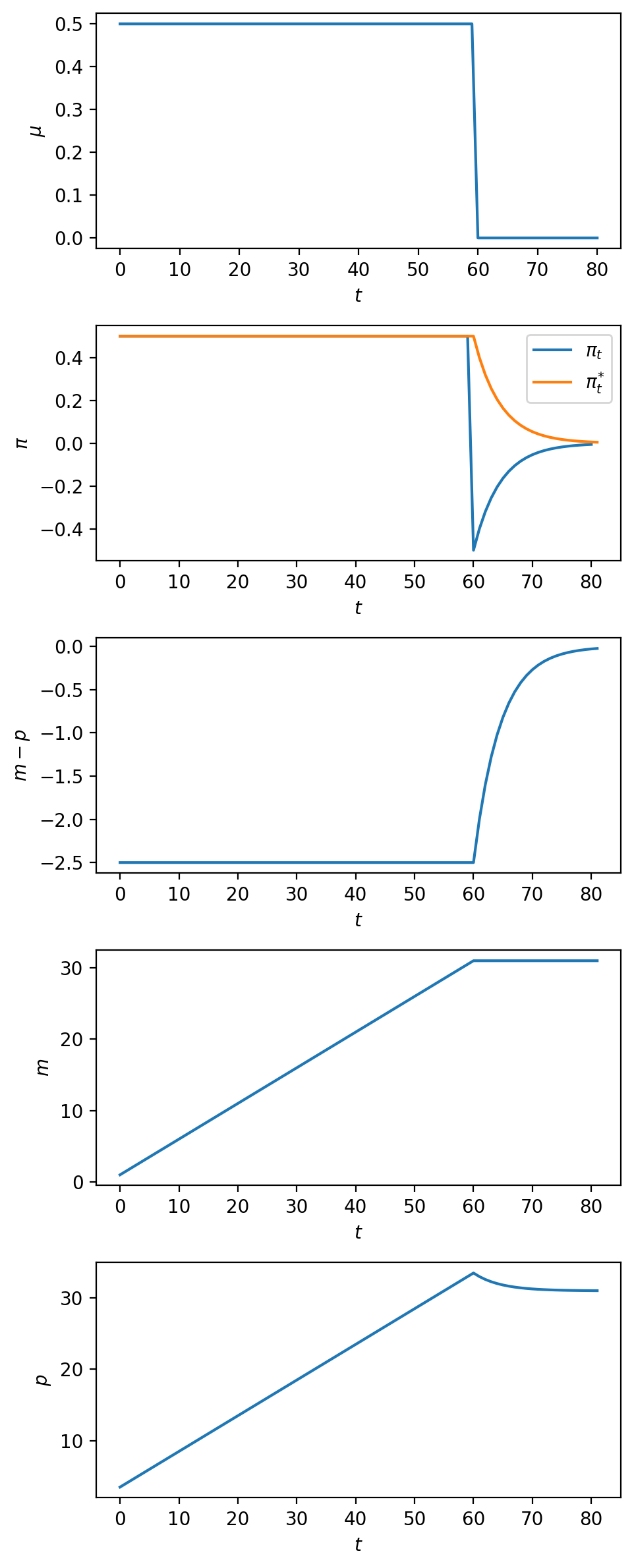
让我们研究一个简单的货币政策变化场景：货币供应增长率最初维持在较高水平\(\mu_0\)，直到时间\(T_1\)时突然降至较低水平\(\mu^*\)并保持不变。

具体来说，假设\(T_1\)是介于0和\(T\)之间的某个时点，且\(\mu_0 > \mu^*\)。货币供应增长率的路径可以写为：

\[\begin{split} \mu_{t+1} = \begin{cases} \mu_0 , & t = 0, \ldots, T_1 -1 \\ \mu^* , & t \geq T_1 \end{cases} \end{split}\]

这个实验与我们在货币主义价格水平理论讲座中分析的情形完全相同。通过对比两个讲座的结果，我们可以清楚地看到采用适应性预期（本讲座）和理性预期（前一讲座）这两种不同预期机制的影响。

μ_seq_1 = np.append(μ0*np.ones(T1), μ_star*np.ones(T+1-T1))

# 求解并绘图
π_seq_1, Eπ_seq_1, m_seq_1, p_seq_1 = solve_and_plot(md, μ_seq_1)

让我们将这些结果与货币主义价格水平理论讲座中的理性预期情形进行对比。

值得注意的是,当货币供应增长率在时间\(T_1\)突然下降时,实际通货膨胀率\(\pi_t\)会”超调”其最终稳态值。这种超调现象在理性预期版本中并不存在,读者可以思考其背后的原因。

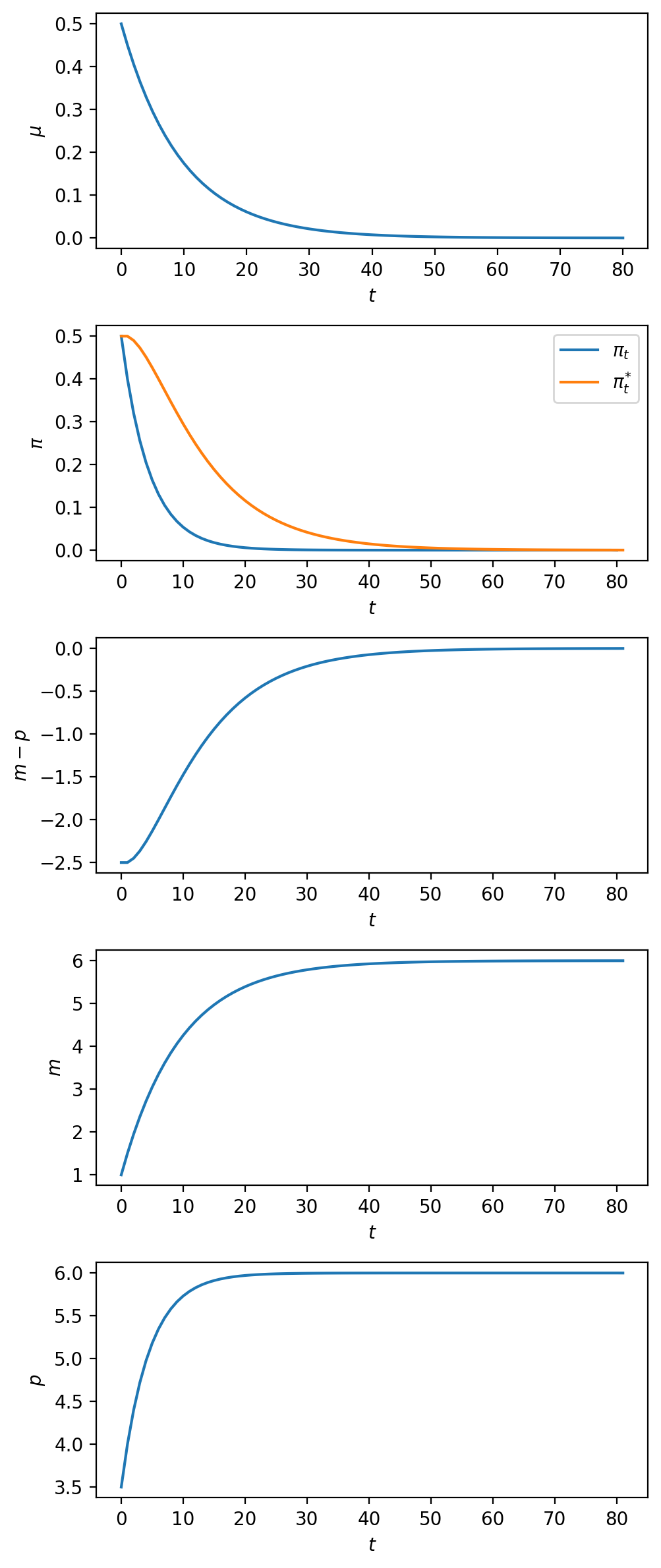
15.6.2. 实验2

接下来我们考虑一个渐进式稳定化的情形,即货币供应增长率从高水平逐步平稳下降到一个较低的水平。

在这种情况下,我们观察到价格水平的通货膨胀率虽然最终会下降,但其下降速度要慢于货币供应增长率的下降速度。

这种通货膨胀率下降缓慢的现象可以归因于从高通胀向低通胀过渡期间,公众的预期通货膨胀率\(\pi_t^*\)始终高于实际通货膨胀率\(\pi_t\)。

# 参数
ϕ = 0.9
μ_seq_2 = np.array([ϕ**t * μ0 + (1-ϕ**t)*μ_star for t in range(T)])
μ_seq_2 = np.append(μ_seq_2, μ_star)


# 求解并绘图
π_seq_2, Eπ_seq_2, m_seq_2, p_seq_2 = solve_and_plot(md, μ_seq_2)