35. 用矩阵代数表示的单变量时间序列#

35.1. 概述#

本讲使用矩阵来解决线性差分方程。

作为一个实际例子，我们将研究一个保罗·萨缪尔森 1939 年文章 [Samuelson, 1939] 中的二阶线性差分方程，该文章引入了乘数加速器模型。

这个模型对早期美国凯恩斯主义宏观经济学的计量经济学研究产生了重要影响。

如果你想了解更多关于这个模型的细节，可以参考Samuelson Multiplier-Accelerator。

（该讲座也包含了二阶线性差分方程的一些技术细节。）

在本讲座中，我们将探讨如何用两种不同的方式来表示非平稳时间序列 ${y_{t}}_{t = 0}^{T}$ ：自回归表示和移动平均表示。

我们还将研究一个涉及解“前瞻性”线性差分方程的“完全预见的”股票价格模型。

让我们先导入所需的Python包：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

# 设置默认图形大小
plt.rcParams["figure.figsize"] = (11, 5)

# 设置打印的浮点数精度
np.set_printoptions(precision=3, suppress=True)

35.2. 萨缪尔森的模型#

设 $t = 0, \pm 1, \pm 2, \dots$ 为时间。

对于 $t = 1, 2, 3, \dots, T$ ，假设

(35.1)#

y_{t} = α_{0} + α_{1} y_{t - 1} + α_{2} y_{t - 2}

我们假设 $y_{0}$ 和 $y_{- 1}$ 是给定的数字，我们将其作为初始条件。

在萨缪尔森的模型中， $y_{t}$ 表示 国民收入 或者 国内生产总值（GDP）在时间 $t$ 的测量值。

方程 (35.1) 称为 二阶线性差分方程，因为它包含了两个滞后值。

实际上，它是 $T$ 个关于 $T$ 个变量 $y_{1}, y_{2}, \dots, y_{T}$ 的线性方程的集合。

Note

为了能够解决一个二阶线性差分方程，我们需要两个边界条件，它们可以采取两个初始条件或两个终端条件或每种各一个的形式。

我们将方程写成堆叠系统

\begin{array}{r} \underset{\equiv A}{\underset{⏟}{[\begin{array}{cccccccc} 1 & 0 & 0 & 0 & \dots & 0 & 0 & 0 \\ - α_{1} & 1 & 0 & 0 & \dots & 0 & 0 & 0 \\ - α_{2} & - α_{1} & 1 & 0 & \dots & 0 & 0 & 0 \\ 0 & - α_{2} & - α_{1} & 1 & \dots & 0 & 0 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & \dots & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & 0 & \dots & - α_{2} & - α_{1} & 1 \end{array}]}} [\begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ y_{4} \\ ⋮ \\ y_{T} \end{array}] = \underset{\equiv b}{\underset{⏟}{[\begin{array}{c} α_{0} + α_{1} y_{0} + α_{2} y_{- 1} \\ α_{0} + α_{2} y_{0} \\ α_{0} \\ α_{0} \\ ⋮ \\ α_{0} \end{array}]}} \end{array}

或者

A y = b

其中

y = [\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{T} \end{matrix}]

显然， $y$ 可以由以下公式计算得出

y = A^{- 1} b

向量 $y$ 是完整的时间路径 ${y_{t}}_{t = 1}^{T}$ 。

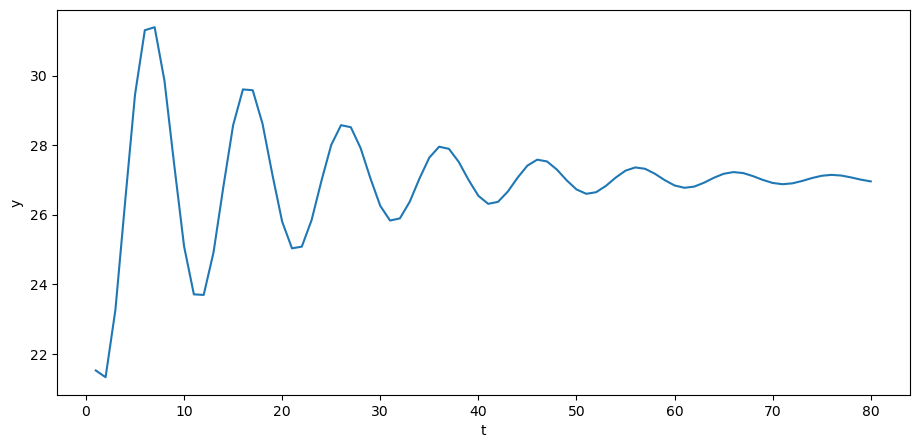
我们用 Python 来实现一个例子来展现萨缪尔森乘数-加速器模型的基本思想。

我们使用与Samuelson Multiplier-Accelerator讲座相同的参数值。

T = 80

# 参数
α_0 = 10.0
α_1 = 1.53
α_2 = -.9

y_neg1 = 28.0 # y_{-1}
y_0 = 24.0

现在我们构造 $A$ 和 $b$ 。

A = np.identity(T)  # T x T 的单位矩阵

for i in range(T):

    if i-1 >= 0:
        A[i, i-1] = -α_1

    if i-2 >= 0:
        A[i, i-2] = -α_2

b = np.full(T, α_0)
b[0] = α_0 + α_1 * y_0 + α_2 * y_neg1
b[1] = α_0 + α_2 * y_0

让我们打印出例子中的矩阵 $A$ 和向量 $b$ 。

A, b

(array([[ 1.  ,  0.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
        [-1.53,  1.  ,  0.  , ...,  0.  ,  0.  ,  0.  ],
        [ 0.9 , -1.53,  1.  , ...,  0.  ,  0.  ,  0.  ],
        ...,
        [ 0.  ,  0.  ,  0.  , ...,  1.  ,  0.  ,  0.  ],
        [ 0.  ,  0.  ,  0.  , ..., -1.53,  1.  ,  0.  ],
        [ 0.  ,  0.  ,  0.  , ...,  0.9 , -1.53,  1.  ]]),
 array([ 21.52, -11.6 ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,
         10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ,  10.  ]))

现在我们来求解 $y$ 的路径。

如果 $y_{t}$ 表示 $t$ 时期的国民生产总值，那么这就是萨缪尔森国民生产总值动态模型的一个版本。

要求解 $y = A^{- 1} b$ ，我们可以直接倒置 $A$

A_inv = np.linalg.inv(A)

y = A_inv @ b

或者我们可以使用 np.linalg.solve：

y_second_method = np.linalg.solve(A, b)

我们确保这两种方法在一定精度下给出相同的结果：

np.allclose(y, y_second_method)

True

$A$ 是可逆的，因为它是下三角且其对角线条目非零

# Check if A is lower triangular
np.allclose(A, np.tril(A))

True

Note

一般来说，np.linalg.solve比使用np.linalg.solve在数值上更稳定。然而，对于这个小例子来说，稳定性不是问题。此外，我们将下面重复使用A_inv，直接计算出它来会有比较好。

现在我们可以绘制时间序列。

plt.plot(np.arange(T)+1, y)
plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/f28b75dd7016499bc59f08d74a2f60c65dc4609fe3feefb3dbaae91a1536e73a.png

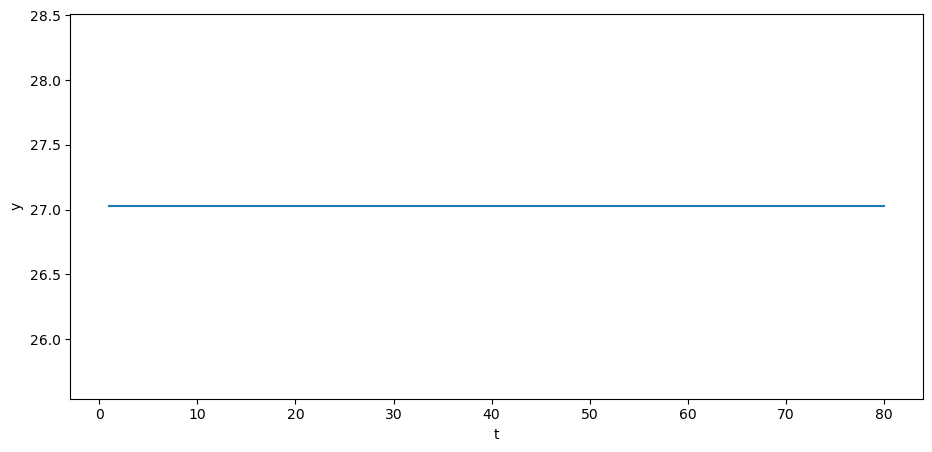
通过在(35.1)中设 $y_{t} = y_{t - 1} = y_{t - 2} = y^{*}$ ，可以得到 $y_{t}$ 的 *稳态* 值 $y^{*}$ 。

y^{*} = \frac{α_{0}}{1 - α_{1} - α_{2}}

如果我们将初始值设为 $y_{0} = y_{- 1} = y^{*}$ ，那么 $y_{t}$ 将是恒定的：

y_star = α_0 / (1 - α_1 - α_2)
y_neg1_steady = y_star # y_{-1}
y_0_steady = y_star

b_steady = np.full(T, α_0)
b_steady[0] = α_0 + α_1 * y_0_steady + α_2 * y_neg1_steady
b_steady[1] = α_0 + α_2 * y_0_steady

y_steady = A_inv @ b_steady

plt.plot(np.arange(T)+1, y_steady)
plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/7c7243db82010ab09792f49b66a7667ec4693c9718ae53d4da6dbf7a50fc5b3b.png

35.3. 添加随机项#

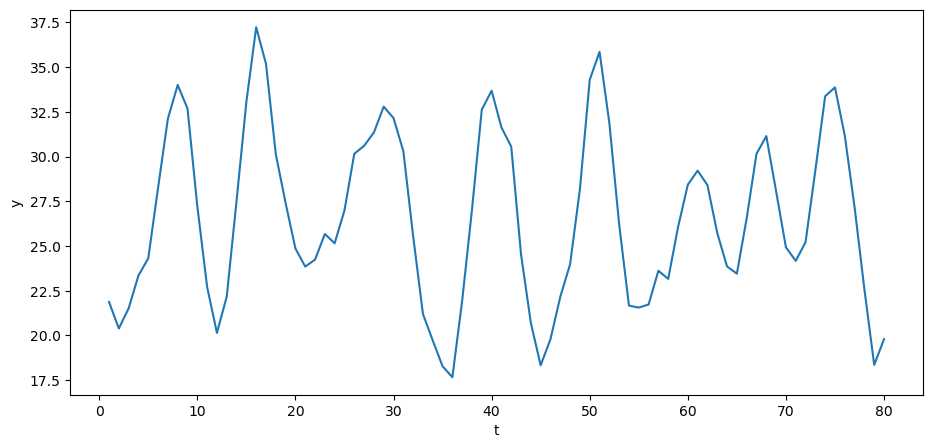
为了让这个例子有趣一些，我们将遵循经济学家尤金·斯卢茨基和拉格纳·弗里希的方法，用以下二阶随机线性差分方程替换我们原来的二阶差分方程：

(35.2)#

y_{t} = α_{0} + α_{1} y_{t - 1} + α_{2} y_{t - 2} + u_{t}

其中 $u_{t} \sim N (0, σ_{u}^{2})$ 并且是独立同分布 – 相互独立且服从相同分布。

我们将把这些 $T$ 个方程堆叠成一个以矩阵代数表示的系统。

让我们定义随机向量

\begin{array}{r} u = [\begin{array}{c} u_{1} \\ u_{2} \\ ⋮ \\ u_{T} \end{array}] \end{array}

其中 $A, b, y$ 定义如上，现在假设 $y$ 由系统

(35.3)#

A y = b + u

所支配

$y$ 的解变为

(35.4)#

y = A^{- 1} (b + u)

让我们在Python中尝试一下。

σ_u = 2.
u = np.random.normal(0, σ_u, size=T)
y = A_inv @ (b + u)

plt.plot(np.arange(T)+1, y)
plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/a5a2dd4208c2f1b92aa781bd03c92cd2c9d054488626e419d537ebbee35c4031.png

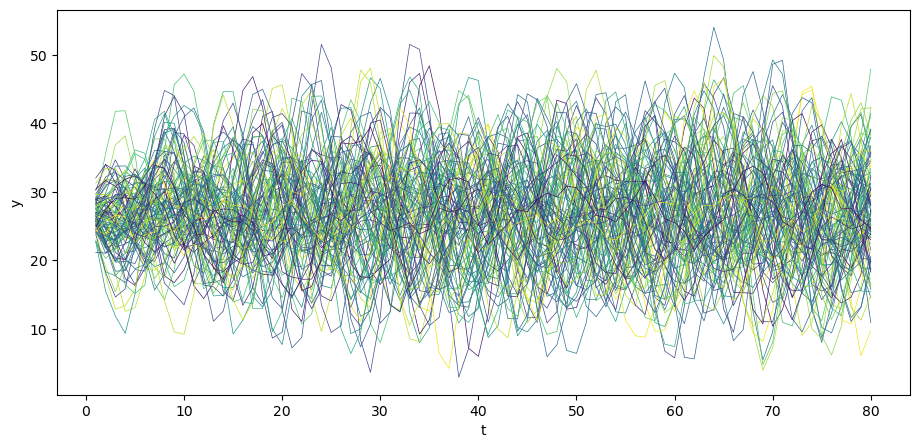
上面生成的时间序列与许多发达国家近几十年的实际GDP数据（去除趋势后）有着惊人的相似性。

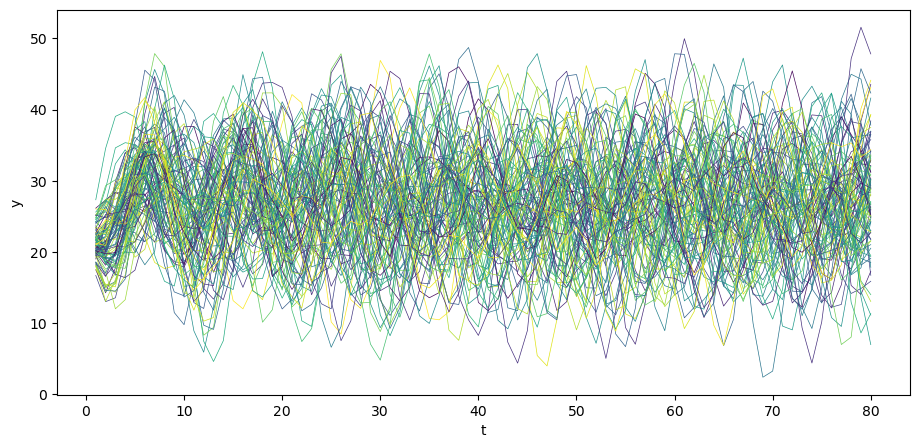
我们可以模拟 $N$ 条路径。

N = 100

for i in range(N):
    col = cm.viridis(np.random.rand())  # 从 viridis 色系中随机选择一种颜色
    u = np.random.normal(0, σ_u, size=T)
    y = A_inv @ (b + u)
    plt.plot(np.arange(T)+1, y, lw=0.5, color=col)

plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/35b55edf20665be131d69efea70194b686ae2e123ca000862464e2e430762a23.png

同样考虑 $y_{0}$ 和 $y_{- 1}$ 处于稳态的情况。

N = 100

for i in range(N):
    col = cm.viridis(np.random.rand())  # 从 viridis 色系中随机选择一种颜色
    u = np.random.normal(0, σ_u, size=T)
    y_steady = A_inv @ (b_steady + u)
    plt.plot(np.arange(T)+1, y_steady, lw=0.5, color=col)

plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/adcd5569ef43ba98c39fd5f01908b586f0fda032c8d97cf75cc2dd86d5922812.png

35.4. 计算总体矩#

我们可以应用多元正态分布的标准公式来计算我们的时间序列模型

y = A^{- 1} (b + u) .

你可以在这篇讲义中阅读关于多元正态分布的内容多元正态分布。

让我们将我们的模型写为

y = \tilde{A} (b + u)

其中 $\tilde{A} = A^{- 1}$ 。

因为正态随机变量的线性组合依然是正态的，我们知道

y \sim N (μ_{y}, Σ_{y})

其中

μ_{y} = \tilde{A} b

以及

Σ_{y} = \tilde{A} (σ_{u}^{2} I_{T \times T}) {\tilde{A}}^{T}

让我们编写一个Python类来计算均值向量 $μ_{y}$ 和协方差矩阵 $Σ_{y}$ 。

class population_moments:
    """
    计算人群矩 mu_y, Sigma_y.
    ---------
    参数:
    alpha0, alpha1, alpha2, T, y_1, y0
    """
    def __init__(self, α_0=10.0, 
                       α_1=1.53, 
                       α_2=-.9, 
                       T=80, 
                       y_neg1=28.0, 
                       y_0=24.0, 
                       σ_u=1):

        # 计算 A
        A = np.identity(T)

        for i in range(T):
            if i-1 >= 0:
                A[i, i-1] = -α_1

            if i-2 >= 0:
                A[i, i-2] = -α_2

        # 计算 b
        b = np.full(T, α_0)
        b[0] = α_0 + α_1 * y_0 + α_2 * y_neg1
        b[1] = α_0 + α_2 * y_0

        # 计算 A 的逆
        A_inv = np.linalg.inv(A)

        self.A, self.b, self.A_inv, self.σ_u, self.T = A, b, A_inv, σ_u, T
    
    def sample_y(self, n):
        """
        提供一个大小为 n 的 y 样本。
        """
        A_inv, σ_u, b, T = self.A_inv, self.σ_u, self.b, self.T
        us = np.random.normal(0, σ_u, size=[n, T])
        ys = np.vstack([A_inv @ (b + u) for u in us])

        return ys

    def get_moments(self):
        """
        计算 y 的总体矩。
        """
        A_inv, σ_u, b = self.A_inv, self.σ_u, self.b

        # 计算 μ_y
        self.μ_y = A_inv @ b
        self.Σ_y = σ_u**2 * (A_inv @ A_inv.T)
        
        return self.μ_y, self.Σ_y


series_process = population_moments()
    
μ_y, Σ_y = series_process.get_moments()
A_inv = series_process.A_inv

接下来，让我们探索不同参数值对 $μ_{y}$ 和 $Σ_{y}$ 的影响。

这个分析也将帮助我们理解一个重要的性质： $y$ 序列的统计平稳性。我们会发现，只有在非常特定的初始条件下，这个序列才是平稳的。

为了直观地理解这一点，我们先生成 $N$ 条 $y$ 序列的样本路径，并将它们与理论均值 $μ_{y}$ 进行对比。

# 绘制均值
N = 100

for i in range(N):
    col = cm.viridis(np.random.rand())  # 从 viridis 色系中随机选择一种颜色
    ys = series_process.sample_y(N)
    plt.plot(ys[i,:], lw=0.5, color=col)
    plt.plot(μ_y, color='red')

plt.xlabel('t')
plt.ylabel('y')

plt.show()

_images/469f4144713c349f02f7fa8e90216242dbdfd2838fb3458912242306b4b5c3ab.png

从图中可以观察到一个有趣的现象：随着时间 $t$ 的推移，不同样本路径之间的离散程度在逐渐减小。

绘制总体方差 $Σ_{y}$ 对角线。

# 绘制方差
plt.plot(Σ_y.diagonal())
plt.show()

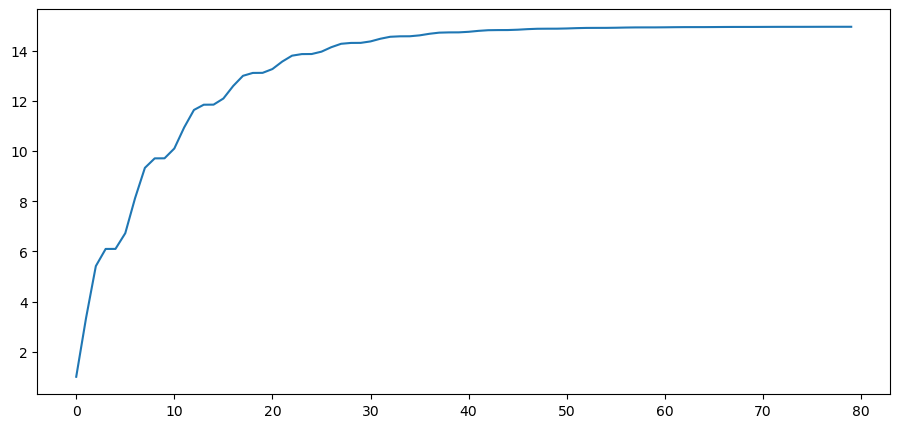
_images/ba7acb839681a83e250f47983bc704e95b6fd1201f2260d3d9f26669189b8aee.png

从图中我们可以看到，总体方差随时间增加，最终趋于一个稳定值。这种收敛行为反映了系统的内在稳定性。

为了进一步验证这一点，让我们通过模拟多条样本路径来计算样本方差，并将其与理论预测进行对比。

series_process = population_moments(α_0=0, 
                                    α_1=.8, 
                                    α_2=0, 
                                    T=6,
                                    y_neg1=0., 
                                    y_0=0., 
                                    σ_u=1)

μ_y, Σ_y = series_process.get_moments()
print("μ_y = ", μ_y)
print("Σ_y = \n", Σ_y)

μ_y =  [0. 0. 0. 0. 0. 0.]
Σ_y = 
 [[1.    0.8   0.64  0.512 0.41  0.328]
 [0.8   1.64  1.312 1.05  0.84  0.672]
 [0.64  1.312 2.05  1.64  1.312 1.049]
 [0.512 1.05  1.64  2.312 1.849 1.48 ]
 [0.41  0.84  1.312 1.849 2.48  1.984]
 [0.328 0.672 1.049 1.48  1.984 2.587]]

观察 $y_{t}$ 和 $y_{t - 1}$ 之间的协方差（即超对角线上的元素），我们发现它们并不相等。

这个特征告诉我们，由 $y$ 向量表示的时间序列不具有平稳性。

要使序列变得平稳，我们需要对系统做一个关键的改变：不再将初始条件 $(y_{0}, y_{- 1})$ 设为固定值，而是让它们服从一个特定的联合正态分布，这个分布具有合适的均值和协方差矩阵。

如果你想了解如何实现这一点，可以参考我们在线性状态空间模型中的详细讨论。

在继续深入分析之前，让我们先来看看 $Σ_{y}$ 矩阵右下角的数值。

series_process = population_moments()
μ_y, Σ_y = series_process.get_moments()

print("bottom right corner of Σ_y = \n", Σ_y[72:,72:])

bottom right corner of Σ_y = 
 [[ 14.965  12.051   4.969  -3.243  -9.434 -11.515  -9.128  -3.602]
 [ 12.051  14.965  12.051   4.969  -3.243  -9.434 -11.515  -9.128]
 [  4.969  12.051  14.966  12.051   4.97   -3.243  -9.434 -11.516]
 [ -3.243   4.969  12.051  14.966  12.052   4.97   -3.243  -9.434]
 [ -9.434  -3.243   4.97   12.052  14.967  12.053   4.97   -3.243]
 [-11.515  -9.434  -3.243   4.97   12.053  14.968  12.053   4.97 ]
 [ -9.128 -11.515  -9.434  -3.243   4.97   12.053  14.968  12.053]
 [ -3.602  -9.128 -11.516  -9.434  -3.243   4.97   12.053  14.968]]

请注意，随着时间 $t$ 的增加，子对角线和超对角线上的元素似乎趋于收敛。

这表明我们的过程是渐近平稳的。

你可以在线性状态空间模型中阅读更多关于更一般线性时间序列模型的平稳性。

通过观察不同时间段的 $Σ_{y}$ 的非对角线元素，我们可以学到很多关于这个过程的知识，但我们在这里暂时先不展开。

35.5. 移动平均表示#

让我们来研究 $A^{- 1}$ 矩阵的结构。这个矩阵的形状会告诉我们一些关于系统动态特性的重要信息。

它是三角形矩阵、接近三角形，还是其他形式 $\dots$ ？

为了便于观察，我们将打印 $A^{- 1}$ 矩阵左上角的一部分，并将数值保留到小数点后三位。

print(A_inv[0:7,0:7])

[[ 1.     0.    -0.    -0.     0.    -0.    -0.   ]
 [ 1.53   1.    -0.    -0.     0.    -0.    -0.   ]
 [ 1.441  1.53   1.     0.     0.     0.     0.   ]
 [ 0.828  1.441  1.53   1.     0.     0.     0.   ]
 [-0.031  0.828  1.441  1.53   1.    -0.    -0.   ]
 [-0.792 -0.031  0.828  1.441  1.53   1.     0.   ]
 [-1.184 -0.792 -0.031  0.828  1.441  1.53   1.   ]]

显然， $A^{- 1}$ 是一个下三角矩阵。

注意每一行的结尾都与前一行的前对角线元素相同。

由于 $A^{- 1}$ 是下三角矩阵，每一行代表特定 $t$ 时的 $y_{t}$ ，作为以下两部分之和：

与初始条件 $b$ 相关的时间依赖函数 $A^{- 1} b$ ，以及
当前和过去 IID 冲击 ${u_{t}}$ 的加权和。

因此，设 $\tilde{A} = A^{- 1}$ 。

显然，对于 $t \geq 0$ ，

y_{t + 1} = \sum_{i = 1}^{t + 1} {\tilde{A}}_{t + 1, i} b_{i} + \sum_{i = 1}^{t} {\tilde{A}}_{t + 1, i} u_{i} + u_{t + 1}

这是一个移动平均表示，其系数随时间变化。

我们可以看到，系统既可以用移动平均形式 (35.4) 表示，也可以用自回归形式 (35.3) 表示。这两种表示方式描述了同一个随机过程，只是从不同的角度来看。

35.6. 从后视到前瞻#

到目前为止，我们分析的萨缪尔森模型是一个后视(backward-looking)模型 - 给定初始条件后，系统就会向前演化。

接下来让我们转向一个*前瞻(forward-looking)*模型，这类模型在宏观经济学和金融学中被广泛使用。

我们应用类似的线性代数工具来研究一个广泛用作宏观经济学和金融学基准的完全预见模型。

例如，假设 $p_{t}$ 是股票价格， $y_{t}$ 是其股息。

假设股息 $y_{t}$ 遵循我们前面分析的二阶差分方程，即

y = A^{- 1} (b + u)

我们的完全预见股票价格模型是

p_{t} = \sum_{j = 0}^{T - t} β^{j} y_{t + j}, β \in (0, 1)

其中 $β$ 是折现因子。

该模型表明，股票在 $t$ 时刻的价格等于从当期开始直到终期所有未来股息的现值之和。每期股息都按折现因子 $β$ 进行贴现，期数越远贴现程度越大。

\begin{array}{r} \underset{\equiv p}{\underset{⏟}{[\begin{array}{c} p_{1} \\ p_{2} \\ p_{3} \\ ⋮ \\ p_{T} \end{array}]}} = \underset{\equiv B}{\underset{⏟}{[\begin{array}{ccccc} 1 & β & β^{2} & \dots & β^{T - 1} \\ 0 & 1 & β & \dots & β^{T - 2} \\ 0 & 0 & 1 & \dots & β^{T - 3} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & \dots & 1 \end{array}]}} [\begin{array}{c} y_{1} \\ y_{2} \\ y_{3} \\ ⋮ \\ y_{T} \end{array}] \end{array}

β = .96

#  构建 B
B = np.zeros((T, T))

for i in range(T):
    B[i, i:] = β ** np.arange(0, T-i)

print(B)

[[1.    0.96  0.922 ... 0.043 0.041 0.04 ]
 [0.    1.    0.96  ... 0.045 0.043 0.041]
 [0.    0.    1.    ... 0.047 0.045 0.043]
 ...
 [0.    0.    0.    ... 1.    0.96  0.922]
 [0.    0.    0.    ... 0.    1.    0.96 ]
 [0.    0.    0.    ... 0.    0.    1.   ]]

σ_u = 0.
u = np.random.normal(0, σ_u, size=T)
y = A_inv @ (b + u)
y_steady = A_inv @ (b_steady + u)

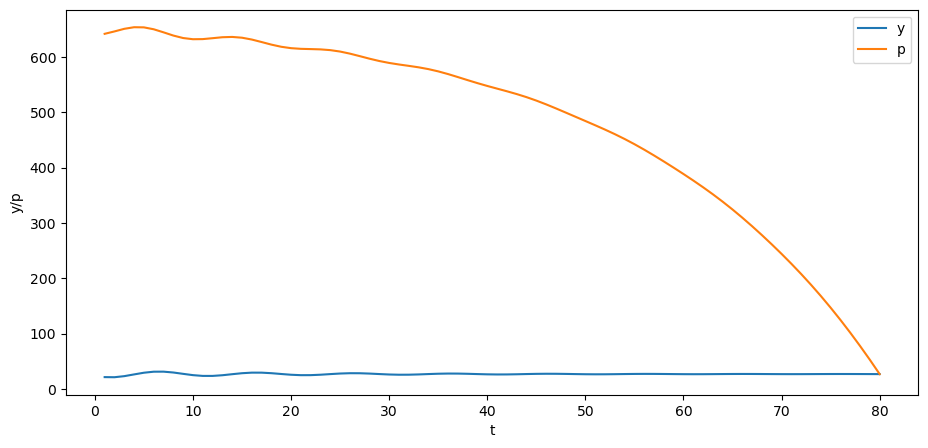
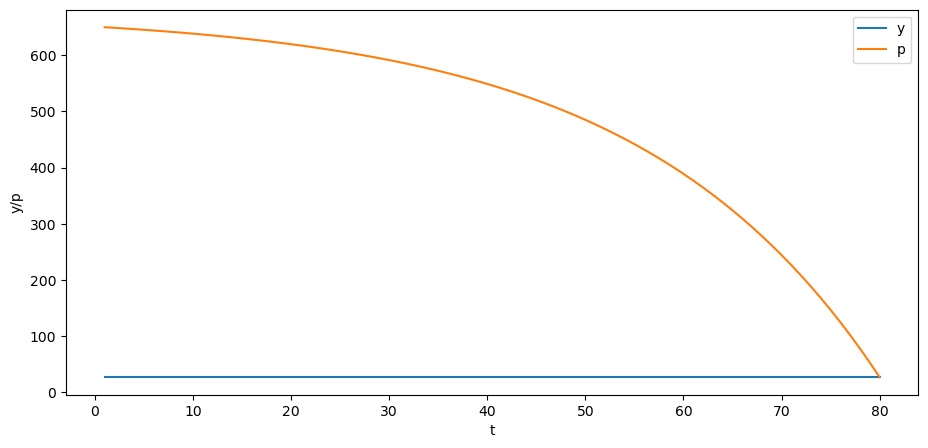
p = B @ y

plt.plot(np.arange(0, T)+1, y, label='y')
plt.plot(np.arange(0, T)+1, p, label='p')
plt.xlabel('t')
plt.ylabel('y/p')
plt.legend()

plt.show()

_images/c17f463d6ea660493cc63382adbca8c66bc703f270681b053bd8ce7f2a17f6e4.png

你能解释一下为什么价格的趋势在随时间下降吗？

接下来还可以考虑当 $y_{0}$ 和 $y_{- 1}$ 处于稳态时的情况。

p_steady = B @ y_steady

plt.plot(np.arange(0, T)+1, y_steady, label='y')
plt.plot(np.arange(0, T)+1, p_steady, label='p')
plt.xlabel('t')
plt.ylabel('y/p')
plt.legend()

plt.show()

_images/b38fbda4ac5c7c8b13ac5741366eb1253d339b0dc6c01e0eadbfdc44f07b56c1.png