40. 就业的湖泊模型#
40.1. 大纲#
除了 Anaconda 中包含的内容外,本讲座还需要以下库:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']
40.2. 湖泊模型#
这个模型有时被称为湖泊模型,因为存在两个工人群体:
当前就业的工人。
当前失业但正在寻找工作的工人。
两个”湖泊”之间的”流动”如下:
工人以 \(d\) 的比率退出劳动力市场。
新工人以 \(b\) 的比率进入劳动力市场。
就业工人以 \(\alpha\) 的比率与工作分离。
失业工人以 \(\lambda\) 的比率找到工作。
下图说明了湖泊模型。
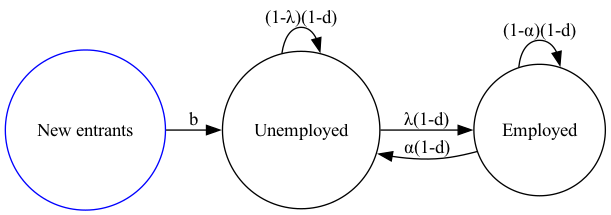
Fig. 40.1 湖泊模型的示意图#
40.3. 动态变化#
设 \(e_t\) 和 \(u_t\) 分别表示在时间 \(t\) 时就业和失业工人的数量。
工人总人口为 \(n_t = e_t + u_t\)。
因此,失业和就业工人的数量按以下方式变化:
我们可以将(40.1)整理为矩阵形式的线性方程组 \(x_{t+1} = Ax_t\),其中
假设在 \(t=0\) 时,我们有 \(x_0 = \begin{bmatrix} u_0 & e_0 \end{bmatrix}^\top\)。
那么,\(x_1=Ax_0\),\(x_2=Ax_1=A^2x_0\),因此 \(x_t = A^tx_0\)。
因此,该系统的长期结果可能取决于初始条件 \(x_0\) 和矩阵 \(A\)。
我们关心 \(u_t\) 和 \(e_t\) 如何随时间如何演变。
失业率和就业率从长期来看会如何变化?
长期结果是否取决于初始值 \((u_0, e_o)\)?
40.3.1. 可视化长期结果#
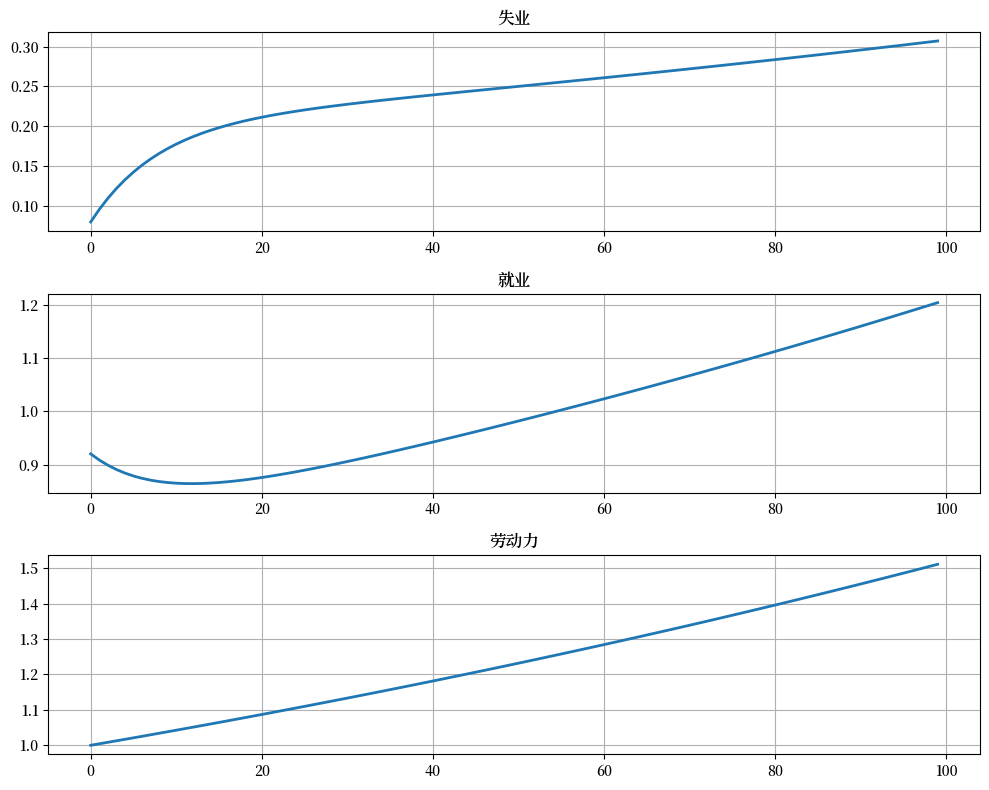
让我们首先绘制失业率 \(u_t\)、就业率 \(e_t\) 和劳动力 \(n_t\) 的时间序列图。
class LakeModel:
"""
求解湖泊模型并计算失业存量和失业率的动态变化。
参数:
------------
λ:标量
当前失业工人的找到工作的比率
α:标量
当前就业工人的解雇率
b:标量
进入劳动力市场的比率
d:标量
退出劳动力市场的比率
"""
def __init__(self, λ=0.1, α=0.013, b=0.0124, d=0.00822):
self.λ, self.α, self.b, self.d = λ, α, b, d
λ, α, b, d = self.λ, self.α, self.b, self.d
self.g = b - d
g = self.g
self.A = np.array([[(1-d)*(1-λ) + b, α*(1-d) + b],
[ (1-d)*λ, (1-α)*(1-d)]])
self.ū = (1 + g - (1 - d) * (1 - α)) / (1 + g - (1 - d) * (1 - α) + (1 - d) * λ)
self.ē = 1 - self.ū
def simulate_path(self, x0, T=1000):
"""
模拟就业和失业的序列
参数
----------
x0:数组
包含初始值 (u0,e0)
T:整数
模拟的周期数
返回值
----------
x:迭代器
包含就业率和失业率的序列
"""
x0 = np.atleast_1d(x0) # 重新转换为数组
x_ts= np.zeros((2, T))
x_ts[:, 0] = x0
for t in range(1, T):
x_ts[:, t] = self.A @ x_ts[:, t-1]
return x_ts
lm = LakeModel()
e_0 = 0.92 # 初始就业
u_0 = 1 - e_0 # 给定初始 n_0 = 1 的情况下的初始失业率
lm = LakeModel()
T = 100 # 模拟时长
x_0 = (u_0, e_0)
x_path = lm.simulate_path(x_0, T)
fig, axes = plt.subplots(3, 1, figsize=(10, 8))
axes[0].plot(x_path[0, :], lw=2)
axes[0].set_title('失业')
axes[1].plot(x_path[1, :], lw=2)
axes[1].set_title('就业')
axes[2].plot(x_path.sum(0), lw=2)
axes[2].set_title('劳动力')
for ax in axes:
ax.grid()
plt.tight_layout()
plt.show()
不出所料,我们观察到劳动力\(n_t\)以恒定的速率增长。
这与只有一个流入源(新进入者池)流向失业和就业池的事实相吻合。
从长期来看,劳动力市场系统的流入和流出是由劳动力市场的恒定退出率和进入率决定的。
具体来说,令 \(\mathbb{1}=[1, 1]^\top\) 为一个全1向量。
我们可以得出
因此,\(n_t\) 的增长率固定为 \(1 + b - d\)。
此外,失业和就业的时间序列似乎在长期内以某些稳定的速率增长。
40.3.2. 佩龙-弗罗贝尼乌斯定理的应用#
从直觉上讲,如果我们将失业池和就业池视为一个封闭系统,其增长应该与劳动力相似。
接下来我们要问,\(e_t\) 和 \(u_t\) 的长期增长率 是否也像劳动力一样主要由 \(1+b-d\) 决定?
如果我们应用佩龙-弗罗贝尼乌斯定理,答案将更加清晰。
佩龙-弗罗贝尼乌斯定理的重要性源于以下事实:
首先,在现实世界中,我们遇到的大多数矩阵都是非负矩阵。
其次,许多重要模型只是线性迭代模型,它们从初始条件\(x_0\)开始,然后通过规则\(x_{t+1} = Ax_t\)或简写为\(x_t = A^tx_0\)递归演化。
这个定理有助于描述主特征值\(r(A)\),它决定了这个迭代过程的行为。
40.3.2.1. 主导特征向量#
现在我们学习如何运用佩龙-弗罗贝尼乌斯定理来帮助我们分析湖泊模型。
由于 \(A\) 是非负且不可约的矩阵,佩龙-弗罗贝尼乌斯定理意味着:
谱半径 \(r(A)\) 是 \(A\) 的一个特征值,其中
任何其他特征值 \(\lambda\) 的绝对值都严格小于 \(r(A)\):\(|\lambda|< r(A)\),
存在唯一且处处正的右特征向量 \(\phi\)(列向量)和左特征向量 \(\psi\)(行向量):
如果进一步假设 \(A\) 是正的,那么当 \(<\psi, \phi> = \psi \phi=1\) 时,我们有
最后一个陈述意味着长期来看,\(A^t\) 的量级与 \(r(A)^t\) 的量级相同,其中 \(r(A)\) 在本讲座中可被视为主特征值。
因此,长期来看,\(x_t = A^t x_0\) 的量级也由 \(r(A)^t\) 主导。
回想一下,谱半径受列和的约束:对于 \(A \geq 0\),我们有
注意,对于 \(j=1,2\),有\(\text{colsum}_j(A) = 1 + b - d\),且根据(40.2),我们可以得出主特征值为 \(r(A) = 1 + b - d\)。
令 \(g = b - d\) 表示总劳动力的整体增长率,因此 \(r(A) = 1 + g\)。
佩龙-弗罗贝尼乌斯定理意味着存在唯一的正特征向量 \(\bar{x} = \begin{bmatrix} \bar{u} \\ \bar{e} \end{bmatrix}\), 使得 \(A\bar{x} = r(A)\bar{x}\) 且 \(\begin{bmatrix} 1 & 1 \end{bmatrix} \bar{x} = 1\):
由于 \(\bar{x}\) 是对应于主特征值 \(r(A)\) 的特征向量,我们称 \(\bar{x}\) 为主特征向量。
这个主特征向量在确定长期结果方面起着重要作用,如下所示。
def plot_time_paths(lm, x0=None, T=1000, ax=None):
"""
绘制模拟的时间序列图。
参数
----------
lm : 类
湖泊模型
x0 : 数组
包含一些不同的初始值。
T : 整数
要模拟的周期数
"""
if x0 is None:
x0 = np.array([[5.0, 0.1]])
ū, ē = lm.ū, lm.ē
x0 = np.atleast_2d(x0)
if ax is None:
fig, ax = plt.subplots(figsize=(10, 8))
# 绘制线$D$
s = 10
ax.plot([0, s * ū], [0, s * ē], "k--", lw=1, label='设置$D$')
# 设置通过原点的坐标轴
for spine in ["left", "bottom"]:
ax.spines[spine].set_position("zero")
for spine in ["right", "top"]:
ax.spines[spine].set_color("none")
ax.set_xlim(-2, 6)
ax.set_ylim(-2, 6)
ax.set_xlabel("失业人群")
ax.set_ylabel("就业人群")
ax.set_xticks((0, 6))
ax.set_yticks((0, 6))
# 绘制时间序列
for x in x0:
x_ts = lm.simulate_path(x0=x)
ax.scatter(x_ts[0, :], x_ts[1, :], s=4,)
u0, e0 = x
ax.plot([u0], [e0], "ko", ms=2, alpha=0.6)
ax.annotate(f'$x_0 = ({u0},{e0})$',
xy=(u0, e0),
xycoords="data",
xytext=(0, 20),
textcoords="offset points",
arrowprops=dict(arrowstyle = "->"))
ax.plot([ū], [ē], "ko", ms=4, alpha=0.6)
ax.annotate(r'$\bar{x}$',
xy=(ū, ē),
xycoords="data",
xytext=(20, -20),
textcoords="offset points",
arrowprops=dict(arrowstyle = "->"))
if ax is None:
plt.show()
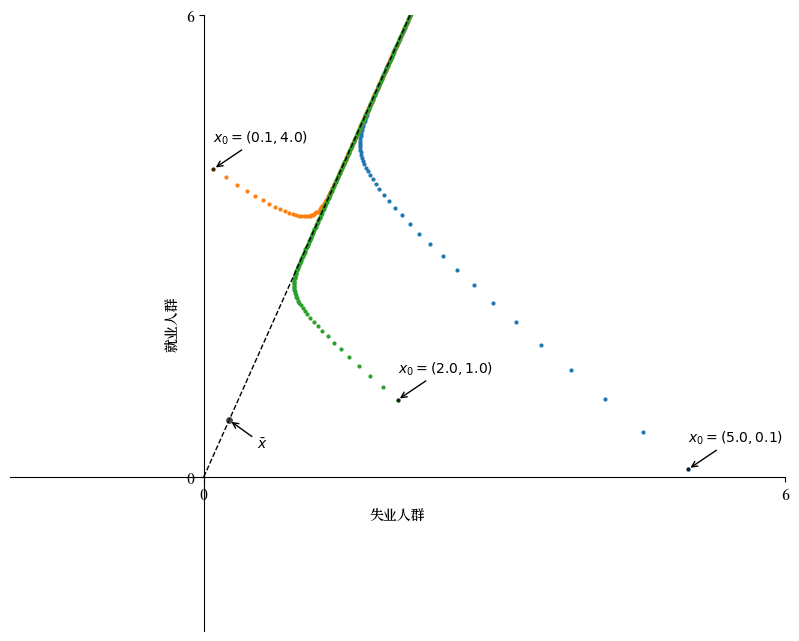
lm = LakeModel(α=0.01, λ=0.1, d=0.02, b=0.025)
x0 = ((5.0, 0.1), (0.1, 4.0), (2.0, 1.0))
plot_time_paths(lm, x0=x0)
由于 \(\bar{x}\) 是对应于特征值 \(r(A)\) 的特征向量,集合 \(D := \{ x \in \mathbb{R}^2 : x = \alpha \bar{x} \; \text{对某些} \; \alpha >0 \}\) 中的所有向量也都是对应于 \(r(A)\) 的特征向量。
这个集合 \(D\) 在上图中由虚线表示。
图中说明了对于两个不同的初始条件 \(x_0\),迭代序列 \((A^t x_0)_{t \geq 0}\) 随时间向 \(D\) 移动。
这表明所有这样的序列在长期内都具有很强的相似性,由主特征向量 \(\bar{x}\) 决定。
40.3.2.2. 负增长率#
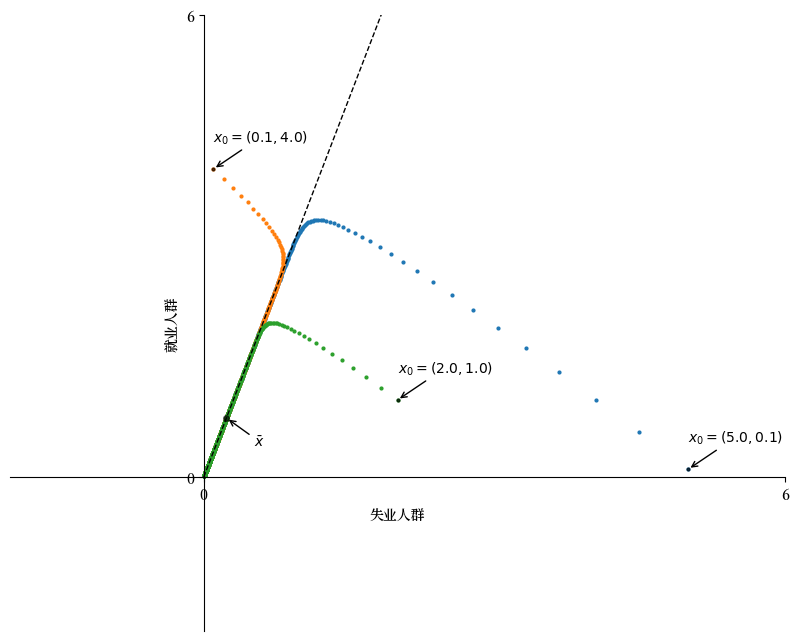
在上面说明的例子中,我们考虑的参数使得劳动力的总体增长率 \(g>0\)。
现在假设我们面临 \(g<0\) 的情况,即劳动力呈负增长。
这意味着 \(b-d<0\),即工人退出市场的速度快于进入市场的速度。
现在迭代序列 \(x_{t+1} = Ax_t\) 的行为会是什么样的?
这在下面进行了可视化。
因此,虽然迭代序列仍然朝着主特征向量 \(\bar{x}\) 移动,但在这种情况下,它们收敛到原点。
这是由于 \(r(A)<1\) 的事实,这确保了迭代序列 \((A^t x_0)_{t \geq 0}\) 将收敛到某个点,在这种情况下是 \((0,0)\)。
这引导我们到下一个结果。
40.3.3. 性质#
由于 \(A\) 的列和为 \(r(A)=1\),左特征向量是 \(\mathbb{1}^\top=[1, 1]\)。
佩龙-弗罗贝尼乌斯理论告诉我们
因此,对于任何 \(x_0 = (u_0, e_0)^\top\),我们有
当 \(t\) 足够大时。
我们看到,在长期内,\(u_t\) 和 \(e_t\) 的增长也由 \(r(A) = 1+g\) 主导:当 \(r(A) > 1\) 时,\(x_t\) 沿着 \(D\) 增长,当 \(r(A) < 1\) 时,收敛到 \((0, 0)\)。
此外,长期失业和就业是 \(n_t\) 的稳定比例。
后者意味着 \(\bar{u}\) 和 \(\bar{e}\) 分别是长期失业率和就业率。
具体来说,当 \(t \to \infty\) 时,我们有失业率和就业率:\(x_t / n_t = A^t n_0 / n_t \to \bar{x}\)。
为了说明这些比率的动态,令 \(\hat{A} := A / (1+g)\) 为 \(r_t := x_t/ n_t\) 的转移矩阵。
比率的动态遵循
注意 \(\hat{A}\) 的列和都为 1,因此 \(r(\hat{A})=1\)。
我们可以验证 \(\bar{x}\) 也是 \(\hat{A}\) 对应于 \(r(\hat{A})\) 的右特征向量,即 \(\bar{x} = \hat{A} \bar{x}\)。
此外,对于任何 \(r_0 = x_0 / n_0\),当 \(t \to \infty\) 时,\(\hat{A}^t r_0 \to \bar{x}\),因为上述讨论意味着
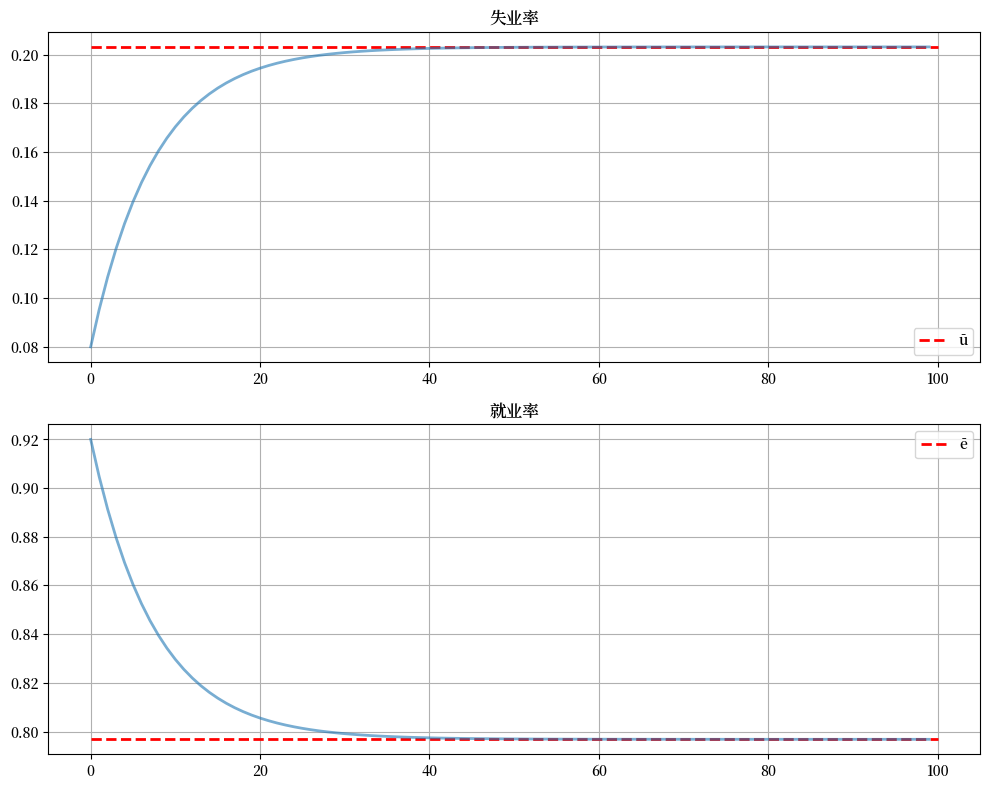
我们用下面的代码来说明
lm = LakeModel()
e_0 = 0.92 # 初始就业
u_0 = 1 - e_0 # 给定初始 n_0 = 1 的情况下的初始失业率
lm = LakeModel()
T = 100 # 模拟时长
x_0 = (u_0, e_0)
x_path = lm.simulate_path(x_0, T)
rate_path = x_path / x_path.sum(0)
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
# 绘制稳态 ū 和 ē
axes[0].hlines(lm.ū, 0, T, 'r', '--', lw=2, label='ū')
axes[1].hlines(lm.ē, 0, T, 'r', '--', lw=2, label='ē')
titles = ['失业率', '就业率']
locations = ['lower right', 'upper right']
# 绘制失业率和就业率
for i, ax in enumerate(axes):
ax.plot(rate_path[i, :], lw=2, alpha=0.6)
ax.set_title(titles[i])
ax.grid()
ax.legend(loc=locations[i])
plt.tight_layout()
plt.show()
为了能更直观地理解收敛性,我们在下面不使用佩龙-弗罗贝尼乌斯定理进一步解释收敛过程。
假设 \(\hat{A} = P D P^{-1}\) 是可对角化的,其中 \(P = [v_1, v_2]\) 由 \(\hat{A}\) 的特征向量 \(v_1\) 和 \(v_2\) 组成, 分别对应于特征值 \(\gamma_1\) 和 \(\gamma_2\), 且 \(D = \text{diag}(\gamma_1, \gamma_2)\)。
令 \(\gamma_1 = r(\hat{A})=1\) 且 \(|\gamma_2| < \gamma_1\),使得谱半径是一个主导特征值。
比率的动态遵循 \(r_{t+1} = \hat{A} r_t\),其中 \(r_0\) 是一个概率向量:\(\sum_j r_{0,j}=1\)。
考虑 \(z_t = P^{-1} r_t \)。
那么,我们有 \(z_{t+1} = P^{-1} r_{t+1} = P^{-1} \hat{A} r_t = P^{-1} \hat{A} P z_t = D z_t\)。
因此,我们得到 \(z_t = D^t z_0\),对于某个 \(z_0 = (c_1, c_2)^\top\),我们有
由于 \(|\gamma_2| < |\gamma_1|=1\),右侧的第二项收敛到零。
因此,收敛过程遵循 \(r_t \to c_1 v_1\)。
由于 \(\hat{A}\) 的列和为 1,且 \(r_0\) 是一个概率向量,\(r_t\) 必须是一个概率向量。
在这种情况下,\(c_1 v_1\) 必须是一个归一化的特征向量,所以 \(c_1 v_1 = \bar{x}\),然后 \(r_t \to \bar{x}\)。
40.4. 练习#
Exercise 40.1 (失业率和就业率的演化)
如果分离率 \(\alpha\) 增加或求职率 \(\lambda\) 下降,长期失业率和就业率会如何演变?
这个结果是否符合你的直觉?
绘制图表来说明直线 \(D := \{ x \in \mathbb{R}^2 : x = \alpha \bar{x} \; \text{对某些} \; \alpha >0 \}\) 在失业-就业空间中如何移动。
Solution to Exercise 40.1 (失业率和就业率的演化)
方程 (40.3) 表明,如果 \(\alpha\) 增加或 \(\lambda\) 减少,长期失业率将会上升,而就业率将会下降。
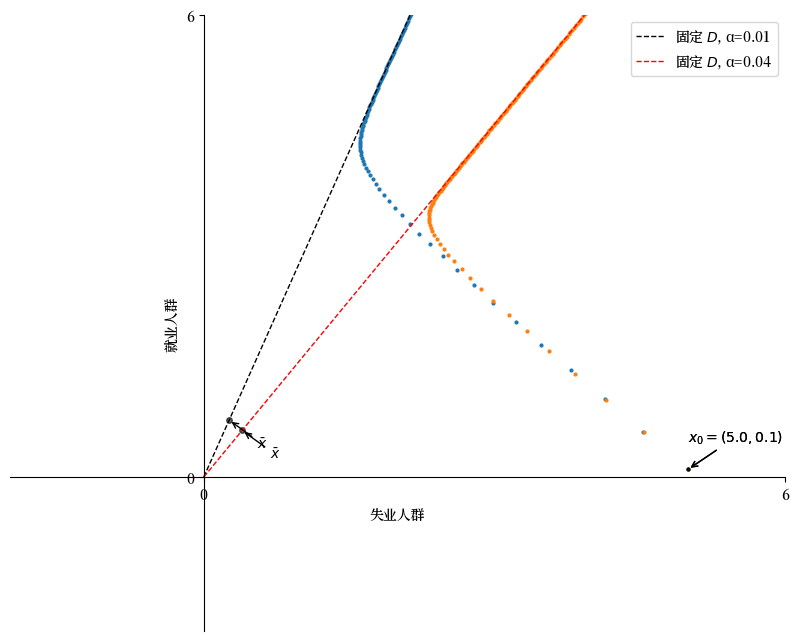
首先假设 \(\alpha=0.01, \lambda=0.1, d=0.02, b=0.025\)。
假设 \(\alpha\) 增加到 \(0.04\)。
下图说明了直线 \(D\) 顺时针向下移动,这表明随着分离率的增加,失业人口的比例上升。
fig, ax = plt.subplots(figsize=(10, 8))
lm = LakeModel(α=0.01, λ=0.1, d=0.02, b=0.025)
plot_time_paths(lm, ax=ax)
s=10
ax.plot([0, s * lm.ū], [0, s * lm.ē], "k--", lw=1, label='固定 $D$, α=0.01')
lm = LakeModel(α=0.04, λ=0.1, d=0.02, b=0.025)
plot_time_paths(lm, ax=ax)
ax.plot([0, s * lm.ū], [0, s * lm.ē], "r--", lw=1, label='固定 $D$, α=0.04')
ax.legend(loc='best')
plt.show()