42. 多种商品的供需关系

42.1. 概览

在之前的讲座中我们研究了一个只有单一消费商品市场的供给、需求和福利。

在这个讲座中，我们将研究有\(n\)种商品及其\(n\)对应价格的情景。

在这次讲座中，我们将遇到的关键基础概念包括：

• 逆需求曲线

• 财富的边际效用

• 逆供给曲线

• 消费者剩余

• 生产者剩余

• 作为消费者剩余和生产者剩余之和的社会福利

• 竞争均衡

我们将提供福利经济学第一定理的一个版本，这个定理是由下列经济学家提出的：

• 莱昂·瓦尔拉斯

• 弗朗西斯·伊西德罗·埃奇沃思

• 维尔弗雷多·帕累托

以下学者为拓展这些关键思想做出了重大贡献：

• 阿巴·勒纳

• 哈罗德·霍特林

• 保罗·萨缪尔森

• 肯尼斯·阿罗

• 热拉尔·德布鲁

我们将描述两个经典的福利定理：

• 第一福利定理： 对于给定的消费者之间的财富分布，竞争均衡下的商品分配方案可以解决社会规划问题。

• 第二福利定理： 如果一个社会规划问题可以找到最优解，那么通过对财富的适当初始分配，就可以通过竞争均衡来实现这个最优解。

如往常一样，我们首先导入一些Python模块。

# 导入一些包
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy.linalg import inv

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

42.2. 来自线性代数的公式

我们将应用线性代数中的公式，这些公式为：

• 对内积中的一个向量求导

• 在矩阵与向量的乘积中对向量本身求导

• 在向量的二次型对中对向量本身求导

这里 \(a\) 为一个 \(n \times 1\) 向量，\(A\) 为一个 \(n \times n\) 矩阵, 且 \(x\) 为一个 \(n \times 1\) 向量:

\[ \frac{\partial a^\top x }{\partial x} = \frac{\partial x^\top a }{\partial x} = a \]

\[ \frac{\partial A x} {\partial x} = A \]

\[ \frac{\partial x^\top A x}{\partial x} = (A + A^\top)x \]

42.3. 从效用函数到需求曲线

我们对消费者的研究将使用以下基本元素：

• \(\Pi\) 是一个 \(m \times n\) 矩阵，

• \(b\) 是一个 \(m \times 1\) 的最优满足点向量，

• \(e\) 是一个 \(n \times 1\) 的禀赋向量，

我们将分析内生对象 \(c\) 和 \(p\)，其中：

• \(c\) 是一个 \(n \times 1\) 各种商品的消费向量，

• \(p\) 是一个 \(n \times 1\) 价格向量

矩阵 \(\Pi\) 描述了消费者将一种商品替换为其他任意一种商品的意愿。

我们假设 \(\Pi\) 的列线性独立，这意味着 \(\Pi^\top \Pi\) 是一个正定矩阵。

• 这意味着 \(\Pi^\top \Pi\) 有一个逆矩阵。

我们将在下面看到，\((\Pi^\top \Pi)^{-1}\) 是一个 \(c\)对价格向量求导的、（补偿）需求曲线斜率矩阵：

\[ \frac{\partial c } {\partial p} = (\Pi^\top \Pi)^{-1} \]

作为价格接受者，消费者面对着价格 \(p\) ，并选择 \(c\) 来最大化效用函数

(42.1)\[ -\frac{1}{2} (\Pi c -b)^\top (\Pi c -b) \]

受到预算约束的限制

(42.2)\[ p^\top (c -e) = 0 \]

我们将指定一些例子，其中 \(\Pi\) 和 \(b\) 的关系通常是这样的：

(42.3)\[ \Pi c \ll b \]

这意味着消费者得到的每种商品的数量都远少于他想要的数量。

在 (42.3) 中的偏差最终将保证竞争性均衡价格是正的。

42.3.1. 隐含约束效用最大化的需求曲线

目前，我们假设预算约束是 (42.2)。

因此，我们将推导出所谓的马歇尔需求曲线。

我们的目标是在约束 (42.2) 下最大化 (42.1)。

构建拉格朗日方程

\[ L = - \frac{1}{2} (\Pi c -b)^T (\Pi c -b ) + \mu [p^T (e-c)] \]

其中 \(\mu\) 是一个拉格朗日乘数，通常被称为财富的边际效用。

消费者选择 \(c\) 来最大化 \(L\)，选择 \(\mu\) 来最小化 \(L\)。

\(c\) 的一阶条件是

\[ \frac{\partial L} {\partial c} = - \Pi^T \Pi c + \Pi^T b - \mu p = 0 \]

因此，给定 \(\mu\)，消费者选择

(42.4)\[ c = (\Pi^T \Pi )^{-1}(\Pi^T b - \mu p ) \]

将 (42.4) 代入预算约束 (42.2) 并解出 \(\mu\) ，可以得到

(42.5)\[ \mu(p,e) = \frac{p^T ( \Pi^T \Pi )^{-1} \Pi^T b - p^T e}{p^T (\Pi^T \Pi )^{-1} p}. \]

等式 (42.5) 描述了财富的边际效用如何依赖于禀赋向量 \(e\) 和价格向量 \(p\)。

Note

等式 (42.5) 是基于约束 \(p^T (c - e) = 0\) 得到的结果。

我们也可以将 \(\mu\) 视为一个参数，并使用 (42.4) 和预算约束 (42.6) 来计算财富。

我们如何进行取决于我们是构建马歇尔需求曲线还是希克斯需求曲线。

42.4. 禀赋经济

我们现在研究一个纯交换经济体————有时被称为禀赋经济。

考虑一个拥有单一消费者和多种商品但没有生产的经济体。

商品的唯一来源是单一消费者的禀赋向量 \(e\)。

一个竞争均衡价格向量促使这个消费者选择 \(c=e\)。

这意味着均衡价格向量满足

\[ p = \mu^{-1} (\Pi^ T b - \Pi^ T \Pi e) \]

在当前这个案例中，我们施加了形式为 (42.2) 的预算约束，由此我们可以通过让财富的边际效用 \(\mu =1\)（或其他任何值）来规范化价格向量。

这相当于选择一个通用单位（或计价单位），在该单位中表达所有商品的价格。

（价格翻倍既不会影响产量也不会影响相对价格。）

我们使 \(\mu=1\)。

Exercise 42.1

证明在 (42.4) 中，使 \(\mu=1\) 意味着满足公式 (42.5)。

Exercise 42.2

证明在 (42.4) 中，使 $\mu=2 依旧意味着满足公式 {eq}eq:old4`。

以下是计算这个经济体竞争均衡的一个类。

class ExchangeEconomy:
    
    def __init__(self,
                 Π,
                 b, 
                 e,
                 thres=1.5):
        """
        设置交换经济体的环境

        参数:
            Π (np.array): 替代共享矩阵
            b (list): 消费者的最优满足点
            e (list): 消费者的禀赋
            thres (float): 检查 p >> Π e 条件的临界值
        """

        # 检查非饱和性
        if np.min(b / np.max(Π @ e)) <= thres:
            raise Exception('将最优满足点设置得更远一些')


        self.Π, self.b, self.e = Π, b, e

    
    def competitive_equilibrium(self):
        """
        计算竞争均衡价格和各商品的分配
        """
        Π, b, e = self.Π, self.b, self.e

        # 计算价格向量，μ=1
        p = Π.T @ b - Π.T @ Π @ e
        
        # 计算消费向量
        slope_dc = inv(Π.T @ Π)
        Π_inv = inv(Π)
        c = Π_inv @ b - slope_dc @ p

        if any(c < 0):
            print(f'分配: {c}')
            raise Exception('负分配：均衡不存在')

        return p, c

42.5. 题外话：马歇尔需求曲线与希克斯需求曲线

有时，我们会在消费者的禀赋向量 \(e\) 是其唯一收入来源的情况下，使用预算约束 (42.2)。

其他时候，我们假设消费者有另外一个收入来源（正或负），并把他的预算约束写为

(42.6)\[ p ^\top (c -e) = w \]

其中 \(w\) 以“美元”（或其他计价单位）衡量，而价格向量的组成部分 \(p_i\) 则以一单位商品 \(i\) 多少美元来衡量。

消费者的财富边际效用取决于消费者的预算约束是 (42.2) 还是 (42.6)， 也取决于将 \(w\) 视为一个自由参数还是一个内生变量。

因此，如何设置 \(\mu\) 决定了我们是在构建

• 马歇尔 需求曲线，此时，我们使用 (42.2) 并使用上述等式 (42.5) 来解 \(\mu\) ，或者

• 希克斯 需求曲线，此时，我们将 \(\mu\) 视为一个固定参数并用 (42.6) 来解 \(w\) 。

马歇尔和希克斯需求曲线考虑的是不同的心理实验：

对于马歇尔需求曲线，假设的价格向量变化引起了替代效应和收入效应

• 收入效应是价格向量变化所引起的 \(p^\top e\) 变动的结果

对于希克斯需求曲线，假设的价格向量变化只引起了替代效应

• 因为我们固定 \(\mu\) 来解出 \(w\)，价格向量的变化不会改变 \(p^\top e + w\)

有时希克斯需求曲线被称为补偿需求曲线，以强调为了消除与价格变化相关的收入（或财富）效应，消费者的财富 \(w\) 被调整。

后面我们将更多地讨论这些不同的需求曲线。

42.6. 作为特殊情况的动态与风险

我们可以创建\(n\)物品纯交换模型的特殊案例来体现：

• 动态 —— 通过在不同的商品上标识不同的日期

• 风险 —— 通过设定商品的交付依赖于世界的状态，这些状态的实现由一个已知的概率分布描述

让我们来具体说明一下。

42.6.1. 动态

假设我们想要表示一个效用函数

\[ - \frac{1}{2} [(c_1 - b_1)^2 + \beta (c_2 - b_2)^2] \]

这里 \(\beta \in (0,1)\) 是一个贴现因子，\(c_1\) 是在时间1的消费，\(c_2\) 是在时间2的消费。

想要用二次效用函数(42.1)来得到上面的式子，需要使

\[ \Pi = \begin{bmatrix} 1 & 0 \cr 0 & \sqrt{\beta} \end{bmatrix} \]

\[ e = \begin{bmatrix} e_1 \cr e_2 \end{bmatrix} \]

以及

\[ b = \begin{bmatrix} b_1 \cr \sqrt{\beta} b_2 \end{bmatrix} \]

预算约束(42.2)变为

\[ p_1 c_1 + p_2 c_2 = p_1 e_1 + p_2 e_2 \]

左侧是消费的贴现现值。

右侧是消费者禀赋的贴现现值。

相对价格 \(\frac{p_1}{p_2}\) 的单位是每单位时间 \(1\) 商品所对应的时间 \(2\) 商品的数量。

因此，

\[ (1+r) := R := \frac{p_1}{p_2} \]

是毛利率，\(r\) 是净利率。

以下是一个例子。

beta = 0.95

Π = np.array([[1, 0],
              [0, np.sqrt(beta)]])

b = np.array([5, np.sqrt(beta) * 5])

e = np.array([1, 1])

dynamics = ExchangeEconomy(Π, b, e)
p, c = dynamics.competitive_equilibrium()

print('竞争均衡价格向量:', p)
print('竞争均衡分配:', c)

竞争均衡价格向量: [4.  3.8]
竞争均衡分配: [1. 1.]

42.6.2. 风险与状态相关权益

我们在静态环境中研究风险，这意味着我们只研究一个时间段。

所谓风险，是指结果事先未知，但受已知概率分布的制约。

例如，我们的消费者面对的风险特别体现在：

• 有两种自然状态，\(1\) 和 \(2\)。

• 消费者知道状态 \(1\) 发生的概率是 \(\lambda\)。

• 消费者知道状态 \(2\) 发生的概率是 \((1-\lambda)\)。

在结果实现之前，消费者的预期效用是

\[ -\frac{1}{2} [\lambda (c_1 - b_1)^2 + (1-\lambda)(c_2 - b_2)^2] \]

其中：

• \(c_1\) 是处于状态 \(1\) 中的消费

• \(c_2\) 是处于状态 \(2\) 中的消费

为了描述这些偏好，我们使

\[ \Pi = \begin{bmatrix} \sqrt{\lambda} & 0 \cr 0 & \sqrt{1-\lambda} \end{bmatrix} \]

\[ e = \begin{bmatrix} e_1 \cr e_2 \end{bmatrix} \]

\[ b = \begin{bmatrix} \sqrt{\lambda}b_1 \cr \sqrt{1-\lambda}b_2 \end{bmatrix} \]

消费者的禀赋向量是

\[ c = \begin{bmatrix} c_1 \cr c_2 \end{bmatrix} \]

价格向量是

\[ p = \begin{bmatrix} p_1 \cr p_2 \end{bmatrix} \]

其中 \(p_i\) 是状态 \(i \in \{1, 2\}\) 下的一单位消费的价格。

交易中的状态依赖型商品（即商品的价值取决于状态值）通常被称为阿罗证券 (Arrow securities)。

在世界的随机状态 \(i\) 实现之前，消费者卖掉他/她的状态依赖型禀赋组合，并购买一个状态依赖型消费组合。

交易此类状态依赖型商品是经济学家常用来模拟保险的方式之一。

我们使用上述技巧将 \(c_1, c_2\) 解释为“阿罗证券”，这是一种即根据不同状态而具有不同价值的消费品索取权。

以下是一个风险经济的实例：

prob = 0.2

Π = np.array([[np.sqrt(prob), 0],
              [0, np.sqrt(1 - prob)]])

b = np.array([np.sqrt(prob) * 5, np.sqrt(1 - prob) * 5])

e = np.array([1, 1])

risk = ExchangeEconomy(Π, b, e)
p, c = risk.competitive_equilibrium()

print('竞争均衡价格向量:', p)
print('竞争均衡分配:', c)

竞争均衡价格向量: [0.8 3.2]
竞争均衡分配: [1. 1.]

Exercise 42.3

考虑上面的实例。

以下每种情况会怎样影响均衡价格和均衡分配，请进行数值分析：

• 消费者变得更穷，

• 他们更喜欢第一种商品，

• 状态 \(1\) 发生的概率更高。

提示：对于每种情况，选择与以上的例子不同的一些参数 \(e, b, \text{或} \lambda\)。

Solution to Exercise 42.3

首先考虑当消费者变得更穷的情况。

这里我们就减少禀赋。

risk.e = np.array([0.5, 0.5])

p, c = risk.competitive_equilibrium()

print('竞争均衡价格向量:', p)
print('竞争均衡分配:', c)

竞争均衡价格向量: [0.9 3.6]
竞争均衡分配: [0.5 0.5]

如果消费者更喜欢第一（或第二）种商品，那么我们可以为商品1设一个更大的最优满足值。

risk.b = np.array([np.sqrt(prob) * 6, np.sqrt(1 - prob) * 5])
p, c = risk.competitive_equilibrium()

print('竞争均衡价格向量:', p)
print('竞争均衡分配:', c)

竞争均衡价格向量: [1.1 3.6]
竞争均衡分配: [0.5 0.5]

增加状态 \(1\) 发生的概率。

prob = 0.8

Π = np.array([[np.sqrt(prob), 0],
              [0, np.sqrt(1 - prob)]])

b = np.array([np.sqrt(prob) * 5, np.sqrt(1 - prob) * 5])

e = np.array([1, 1])

risk = ExchangeEconomy(Π, b, e)
p, c = risk.competitive_equilibrium()

print('竞争均衡价格向量:', p)
print('竞争均衡分配:', c)

竞争均衡价格向量: [3.2 0.8]
竞争均衡分配: [1. 1.]

42.7. 具有内生供应的经济体

迄今为止，我们描述的是一个纯交换经济体，其中商品的禀赋是外生的，意味着它们是模型之外的因素。

42.7.1. 竞争性公司的供给曲线

竞争性公司生产商品，商品的价格向量 \(p\) 是既定的，并选择数量 \(q\)，来最大化总收入减去总成本的值。

因为商品价格向量对于竞争性公司来说是既定的，所以我们称它为价格接受者，在下文中我们用价格接受型竞争性公司来表示。

公司的总收入等于 \(p^T q\)，其总成本等于 \(C(q)\)，其中 \(C(q)\) 是总成本函数

\[ C(q) = h^T q + \frac{1}{2} q^T J q \]

其中 \(J\) 是一个正定矩阵。

因此公司的利润是

(42.7)\[ p^T q - C(q) \]

一个 \(n \times 1\) 的边际成本向量是

\[ \frac{\partial C(q)}{\partial q} = h + H q \]

其中

\[ H = \frac{1}{2} (J + J^T) \]

公司通过将边际收入等于边际成本来最大化总利润。

对于价格接受型公司，一个 \(n \times 1\) 的边际收入向量是 \(\frac{\partial p^T q} {\partial q} = p \)。

因此，对于这个价格接受型竞争性公司，价格等于边际收入。

这产生了以下的竞争性公司的逆供给曲线：

\[ p = h + H q \]

42.7.2. 竞争均衡

对于一个需求曲线由财富边际效用 \(\mu\) 确定的生产型经济体，为了计算它的竞争性均衡，我们首先通过解决规划问题来计算分配问题。

然后，我们使用逆需求曲线或逆供给曲线来计算均衡价格向量。

42.7.2.1. 热身：\(\mu=1\)

作为一个特殊情况，我们通过让财富的边际效用 \(\mu =1\) 来确定一个需求曲线。

让供给价格等于需求价格，并使 \(q=c\)，我们可以得到

\[ p = h + H c = \Pi^{\top} b - \Pi^{\top} \Pi c, \]

这意味着均衡产量向量是

(42.8)\[ c = (\Pi^{\top} \Pi + H )^{-1} ( \Pi^{\top} b - h) \]

这个等式和我们开始时标量 \(n=1\) 的模型中的均衡产量 (7.3) 相对应。

42.7.2.2. 一般情况： \(\mu \neq 1\)

现在，让我们使 \(\mu \neq 1\)，来扩展前面的分析。

由此，逆需求曲线为

(42.9)\[ p = \mu^{-1} [\Pi^{\top} b - \Pi^{\top} \Pi c] \]

使这个等式等于逆供给曲线，让 \(q=c\) 并解出 \(c\) 得

(42.10)\[ c = [\Pi^{\top} \Pi + \mu H]^{-1} [ \Pi^{\top} b - \mu h] \]

42.7.3. 实践

生产型经济体包括：

• 一个可以被理解为代表性消费者的个人

• 一组生产成本

• 一个在规划者福利函数中衡量“消费者”与“生产者”权重的权重因子 \(\mu\)，如上文所述

• 一个 \(n \times 1\) 向量 \(p\)，代表竞争均衡价格

• 一个 \(n \times 1\) 向量 \(c\)，代表竞争均衡数量

• 消费者剩余

• 生产者剩余

这里我们定义一个类 ProductionEconomy。

class ProductionEconomy:
    
    def __init__(self, 
                 Π, 
                 b, 
                 h, 
                 J, 
                 μ):
        """
        设置生产型经济体的环境

        参数:
            Π (np.ndarray): 替代矩阵
            b (np.array): 最优满足点
            h (np.array): 成本函数中的 h
            J (np.ndarray): 成本函数中的 J
            μ (float): 对应规划问题中的福利权重
        """
        self.n = len(b)
        self.Π, self.b, self.h, self.J, self.μ = Π, b, h, J, μ
        
    def competitive_equilibrium(self):
        """
        计算生产型经济体的竞争均衡
        """
        Π, b, h, μ, J = self.Π, self.b, self.h, self.μ, self.J
        H = .5 * (J + J.T)

        # 配置分配
        c = inv(Π.T @ Π + μ * H) @ (Π.T @ b - μ * h)

        # 计算价格
        p = 1 / μ * (Π.T @ b - Π.T @ Π @ c)

        # 检查非饱和
        if any(Π @ c - b >= 0):
            raise Exception('无效结果：将最优满足点设置得更远一些')

        return c, p

    def compute_surplus(self):
        """
        计算单一商品情况下的消费者剩余和生产者剩余
        """
        if self.n != 1:
            raise Exception('不是单一商品')
        h, J, Π, b, μ = self.h.item(), self.J.item(), self.Π.item(), self.b.item(), self.μ
        H = J

        # 供给曲线/需求曲线的系数
        s0, s1 = h, H
        d0, d1 = 1 / μ * Π * b, 1 / μ * Π**2

        # 竞争均衡
        c, p = self.competitive_equilibrium()

        # 计算剩余
        c_surplus = d0 * c - .5 * d1 * c**2 - p * c
        p_surplus = p * c - s0 * c - .5 * s1 * c**2

        return c_surplus, p_surplus

然后定义一个函数，用于绘制需求曲线和供给曲线，并标注剩余和均衡点。

Show source

Hide code cell source

def plot_competitive_equilibrium(PE):
    """
    绘制需求曲线和供给曲线，生产者/消费者剩余以及单一商品生产型经济体的均衡点

    参数:
        PE (class): 初始化的生产型经济体的类
    """
    # 获取单一值
    J, h, Π, b, μ = PE.J.item(), PE.h.item(), PE.Π.item(), PE.b.item(), PE.μ
    H = J

    # 计算竞争均衡
    c, p = PE.competitive_equilibrium()
    c, p = c.item(), p.item()

    # 逆供给/逆需求曲线
    supply_inv = lambda x: h + H * x
    demand_inv = lambda x: 1 / μ * (Π * b - Π * Π * x)

    xs = np.linspace(0, 2 * c, 100)
    ps = np.ones(100) * p
    supply_curve = supply_inv(xs)
    demand_curve = demand_inv(xs)

    # 绘图
    plt.figure()
    plt.plot(xs, supply_curve, label='供给曲线', color='#020060')
    plt.plot(xs, demand_curve, label='需求曲线', color='#600001')

    plt.fill_between(xs[xs <= c], demand_curve[xs <= c], ps[xs <= c], label='消费者剩余', color='#EED1CF')
    plt.fill_between(xs[xs <= c], supply_curve[xs <= c], ps[xs <= c], label='生产者剩余', color='#E6E6F5')

    plt.vlines(c, 0, p, linestyle="dashed", color='black', alpha=0.7)
    plt.hlines(p, 0, c, linestyle="dashed", color='black', alpha=0.7)
    plt.scatter(c, p, zorder=10, label='竞争均衡', color='#600001')

    plt.legend(loc='upper right')
    plt.margins(x=0, y=0)
    plt.ylim(0)
    plt.xlabel('产量')
    plt.ylabel('价格')
    plt.show()

42.7.3.1. 示例：单一经济体与单一商品和生产

现在，我们来构建一个包含单一商品的生产经济体。

为此我们需要：

• 指定一个个人和一个成本曲线，以复现我们开始时用到的简单单一商品供求的示例

• 计算均衡 \(p\) 和 \(c\)，以及消费者剩余和生产者剩余

• 绘制这两种剩余的图

• 改变 \(b\) 从而探究 \(p, c\) 如何变化

Π = np.array([[1]])  # 矩阵现在是一个单一值
b = np.array([10])
h = np.array([0.5])
J = np.array([[1]])
μ = 1

PE = ProductionEconomy(Π, b, h, J, μ)
c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p.item())
print('竞争均衡分配:', c.item())

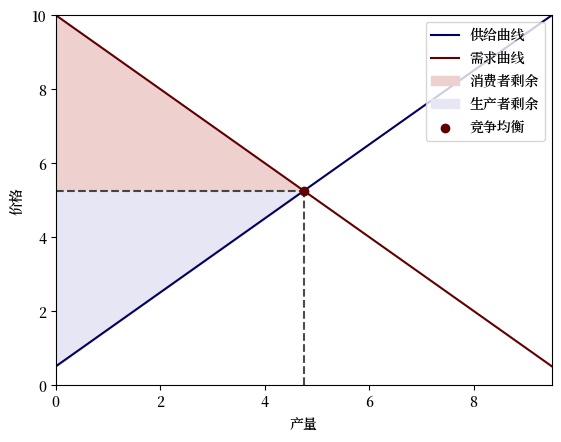
plot_competitive_equilibrium(PE)

竞争均衡价格: 5.25
竞争均衡分配: 4.75

c_surplus, p_surplus = PE.compute_surplus()

print('消费者剩余:', c_surplus.item())
print('生产者剩余:', p_surplus.item())

消费者剩余: 11.28125
生产者剩余: 11.28125

通过提高 \(\mu\) 来降低消费者的福利权重。

PE.μ = 2
c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p.item())
print('竞争均衡分配:', c.item())

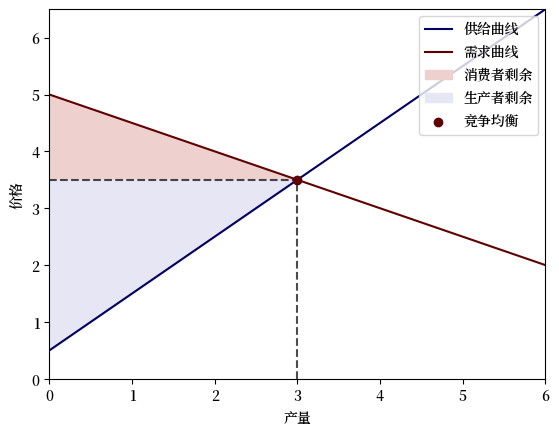
plot_competitive_equilibrium(PE)

竞争均衡价格: 3.5
竞争均衡分配: 3.0

c_surplus, p_surplus = PE.compute_surplus()

print('消费者剩余:', c_surplus.item())
print('生产者剩余:', p_surplus.item())

消费者剩余: 2.25
生产者剩余: 4.5

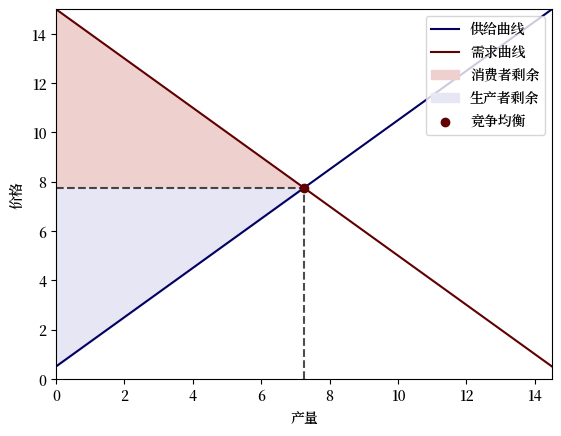
现在我们改变最优满足点，使消费者从消费中获得更多的效用。

PE.μ = 1
PE.b = PE.b * 1.5
c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p.item())
print('竞争均衡分配:', c.item())

plot_competitive_equilibrium(PE)

竞争均衡价格: 7.75
竞争均衡分配: 7.25

这将提高均衡价格和均衡产量。

42.7.3.2. 示例：单个主体、两个商品且包含生产的经济体系

• 我们将进行一些类似上面的实验

• 我们可以使用对角矩阵 \(\Pi\) ，也可以使用非对角矩阵 \(\Pi\) 矩阵来做实验，来研究交叉斜率如何影响 \(p\) 和 \(c\) 对 \(b\) 的各种变化的反应。

Π = np.array([[1, 0],
              [0, 1]])

b = np.array([10, 10])

h = np.array([0.5, 0.5])

J = np.array([[1, 0.5],
              [0.5, 1]])
μ = 1

PE = ProductionEconomy(Π, b, h, J, μ)
c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p)
print('竞争均衡分配:', c)

竞争均衡价格: [6.2 6.2]
竞争均衡分配: [3.8 3.8]

PE.b = np.array([12, 10])

c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p)
print('竞争均衡分配:', c)

竞争均衡价格: [7.13333333 6.46666667]
竞争均衡分配: [4.86666667 3.53333333]

PE.Π = np.array([[1, 0.5],
                 [0.5, 1]])

PE.b = np.array([10, 10])

c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p)
print('竞争均衡分配:', c)

竞争均衡价格: [6.3 6.3]
竞争均衡分配: [3.86666667 3.86666667]

PE.b = np.array([12, 10])
c, p = PE.competitive_equilibrium()

print('竞争均衡价格:', p)
print('竞争均衡分配:', c)

竞争均衡价格: [7.23333333 6.56666667]
竞争均衡分配: [4.93333333 3.6       ]

42.7.4. 题外话：垄断供应商

竞争性公司是一个价格接受者，因此其边际收入是无法由自己控制的。

垄断者知道他们没有竞争对手，可以通过设定产量来影响价格及其边际收入。

垄断者认为自己无法控制需求曲线，而不是价格。

因此，垄断者不是价格接受者，而是在逆需求曲线(42.9)的约束下，设定价格来最大化利润。

所以垄断者的总利润（关于其产量\(q\)的函数）是

(42.11)\[ [\mu^{-1} \Pi^{\text{top}} (b - \Pi q)]^{\text{top}} q - h^{\text{top}} q - \frac{1}{2} q^{\text{top}} J q \]

在找到关于\(q\)的、使垄断者利润最大化的一阶必要条件并求解\(q\)之后，我们发现垄断者设定的产量为

(42.12)\[ q = (H + 2 \mu^{-1} \Pi^{\text{top}} \Pi)^{-1} (\mu^{-1} \Pi^{\text{top}} b - h) \]

我们很快会看到，一个垄断者设置的产量\(q\)比以下任何情况都要低：

• 社会规划者选择\(q\)来最大化社会福利

• 竞争均衡

Exercise 42.4

请证明垄断者的供给曲线是 (42.12)。

42.7.5. 垄断者

我们来考虑一个垄断供应商。

我们在 ProductionEconomy 的类中加入了一个方法，来计算供应商作为垄断者时的均衡价格和均衡分配。

由于供应商现在拥有设定价格的权力：

• 我们首先计算解决垄断者利润最大化问题的最优产量。

• 然后我们从消费者的逆需求曲线中推导出一个均衡价格。

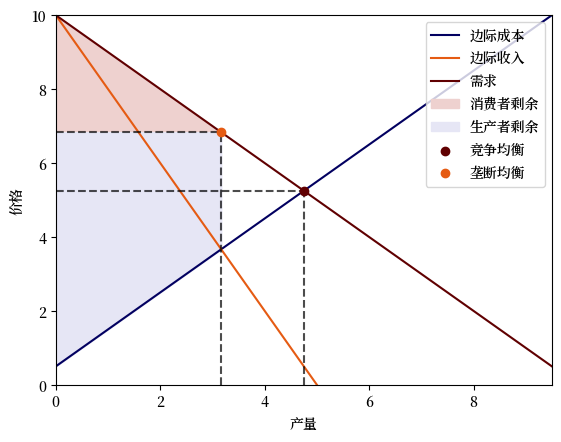
接下来，我们用一个图来展示单一商品情况下，竞争均衡和垄断供应商均衡之间的区别。

回忆一下，在竞争均衡中，一个价格接受型供应商会使边际收入 \(p\) 等于边际成本 \(h + Hq\)。

这就得出了竞争性生产者的逆供给曲线。

垄断者的边际收入不是常数，而是一个依赖于垄断者设定的产量的非平凡函数。

垄断者的边际收入为

\[ MR(q) = -2\mu^{-1}\Pi^{\text{top}}\Pi q+\mu^{-1}\Pi^{\text{top}}b, \]

垄断者使这个边际收入等于其边际成本。

该图显示，垄断者设定的产量低于竞争均衡量。

在单一商品情况下，这种均衡与商品的更高价格相关。

class Monopoly(ProductionEconomy):
    
    def __init__(self, 
                 Π, 
                 b, 
                 h, 
                 J, 
                 μ):
        """
        继承ProductionEconomy类的所有属性和方法
        """
        super().__init__(Π, b, h, J, μ)
        

    def equilibrium_with_monopoly(self):
        """
        在有垄断供应商的情况下计算均衡价格和均衡分配
        """
        Π, b, h, μ, J = self.Π, self.b, self.h, self.μ, self.J
        H = .5 * (J + J.T)

        # 分配
        q = inv(μ * H + 2 * Π.T @ Π) @ (Π.T @ b - μ * h)

        # 价格
        p = 1 / μ * (Π.T @ b - Π.T @ Π @ q)

        if any(Π @ q - b >= 0):
            raise Exception('无效结果：将最优满足点设置得更远一些')

        return q, p

定义一个函数，绘制需求曲线、边际成本曲线以及边际收入曲线，并标注出剩余和均衡点。

Show source

Hide code cell source

def plot_monopoly(M):
    """
    在具有垄断供应商的单一商品经济的情况下，绘制需求曲线、边际生产成本、边际收入、剩余以及均衡的情况

    参数：
        M (class): 继承单一商品垄断经济类ProductionEconomy的类
    """
    # 获取单一值
    J, h, Π, b, μ = M.J.item(), M.h.item(), M.Π.item(), M.b.item(), M.μ
    H = J

    # 计算竞争均衡
    c, p = M.competitive_equilibrium()
    q, pm = M.equilibrium_with_monopoly()
    c, p, q, pm = c.item(), p.item(), q.item(), pm.item()

    # 计算

    # 逆供给/需求曲线
    marg_cost = lambda x: h + H * x  # 边际成本
    marg_rev = lambda x: -2 * 1 / μ * Π * Π * x + 1 / μ * Π * b  # 边际收入
    demand_inv = lambda x: 1 / μ * (Π * b - Π * Π * x)  # 需求曲线

    xs = np.linspace(0, 2 * c, 100)
    pms = np.ones(100) * pm
    marg_cost_curve = marg_cost(xs)
    marg_rev_curve = marg_rev(xs)
    demand_curve = demand_inv(xs)

    # 绘图
    plt.figure()
    plt.plot(xs, marg_cost_curve, label='边际成本', color='#020060')
    plt.plot(xs, marg_rev_curve, label='边际收入', color='#E55B13')
    plt.plot(xs, demand_curve, label='需求', color='#600001')

    plt.fill_between(xs[xs <= q], demand_curve[xs <= q], pms[xs <= q], label='消费者剩余', color='#EED1CF')
    plt.fill_between(xs[xs <= q], marg_cost_curve[xs <= q], pms[xs <= q], label='生产者剩余', color='#E6E6F5')

    plt.vlines(c, 0, p, linestyle="dashed", color='black', alpha=0.7)
    plt.hlines(p, 0, c, linestyle="dashed", color='black', alpha=0.7)
    plt.scatter(c, p, zorder=10, label='竞争均衡', color='#600001')

    plt.vlines(q, 0, pm, linestyle="dashed", color='black', alpha=0.7)
    plt.hlines(pm, 0, q, linestyle="dashed", color='black', alpha=0.7)
    plt.scatter(q, pm, zorder=10, label='垄断均衡', color='#E55B13')

    plt.legend(loc='upper right')
    plt.margins(x=0, y=0)
    plt.ylim(0)
    plt.xlabel('产量')
    plt.ylabel('价格')
    plt.show()

42.7.5.1. 多种商品的例子

让我们在一个拥有多种商品的经济体中比较竞争均衡和垄断结果。

Π = np.array([[1, 0],
              [0, 1.2]])

b = np.array([10, 10])

h = np.array([0.5, 0.5])

J = np.array([[1, 0.5],
              [0.5, 1]])
μ = 1

M = Monopoly(Π, b, h, J, μ)
c, p = M.competitive_equilibrium()
q, pm = M.equilibrium_with_monopoly()

print('竞争均衡价格:', p)
print('竞争均衡分配:', c)

print('垄断供应商的均衡价格:', pm)
print('垄断供应商的均衡分配:', q)

竞争均衡价格: [6.23542117 6.32397408]
竞争均衡分配: [3.76457883 3.94168467]
垄断供应商的均衡价格: [7.26865672 8.23880597]
垄断供应商的均衡分配: [2.73134328 2.6119403 ]

42.7.5.2. 单一商品的例子

Π = np.array([[1]])  # 现在矩阵是一个单一值
b = np.array([10])
h = np.array([0.5])
J = np.array([[1]])
μ = 1

M = Monopoly(Π, b, h, J, μ)
c, p = M.competitive_equilibrium()
q, pm = M.equilibrium_with_monopoly()

print('竞争均衡价格:', p.item())
print('竞争均衡分配:', c.item())

print('垄断供应商的均衡价格:', pm.item())
print('垄断供应商的均衡分配:', q.item())

plot_monopoly(M)

竞争均衡价格: 5.25
竞争均衡分配: 4.75
垄断供应商的均衡价格: 6.833333333333334
垄断供应商的均衡分配: 3.1666666666666665

42.8. 多种商品的福利最大化问题

福利最大化问题 – 有时也被称为社会规划问题 – 是选择 \(c\) 来最大化

\[ - \frac{1}{2} \mu^{-1}(\Pi c -b)^\top (\Pi c -b) \]

减去逆供给曲线下的面积，即，

\[ h c + \frac{1}{2} c^\top J c \]

所以福利标准是

\[ - \frac{1}{2} \mu^{-1}(\Pi c -b)^\top (\Pi c -b) -h c - \frac{1}{2} c^\top J c \]

在这个公式中，\(\mu\) 是一个参数，描述了规划者如何权衡外部供应商和代表性消费者的利益。

对 \(c\) 的一阶条件是

\[ - \mu^{-1} \Pi^\top \Pi c + \mu^{-1}\Pi^\top b - h - J c = 0 \]

这意味着 (42.10) 被满足。

因此，与单一商品的情况一样，对于多种商品情况，竞争均衡下的产量向量可以解决规划问题。

（这是第一福利定理的另一个版本。）

我们可以从以下两个地方推导出竞争均衡的价格向量：

• 逆需求曲线，或

• 逆供给曲线