14. 货币主义价格水平理论#

14.1. 概述#

我们将先用线性代数分析”货币主义价格水平理论”，然后对这个理论进行一系列实验。

这个理论之所以被称为价格水平的”货币”或”货币主义”理论，是因为它认为价格水平的变化源于中央银行对货币供应量的控制。其基本逻辑是：

政府的财政政策决定支出是否超过税收
当支出超过税收时，政府可能会要求中央银行通过印钞来填补这个缺口
这会引发价格水平的变化，直到货币供给与货币需求达到平衡

托马斯·萨金特和尼尔·华莱士在[Sargent, 2013]第5章（重印自1981年明尼阿波利斯联储的文章《令人不快的货币主义算术》）中详细阐述了这一理论。

这个理论有时也被称为”价格水平的财政理论”，强调了财政赤字在影响货币供应变化中的核心作用。约翰·科克伦[Cochrane, 2023]对该理论进行了进一步的发展、评析和应用。

在另一个讲座价格水平历史中，我们探讨了第一次世界大战后欧洲的几次恶性通货膨胀。

价格水平财政理论的核心机制有助于我们理解这些历史事件。

该理论指出，当政府长期支出超过税收并通过印钞融资（即”财政赤字”）时，就会推高价格水平，导致持续通货膨胀。

“货币主义”或”价格水平的财政理论”的两个核心论断：

持续通货膨胀始于政府持续通过印钞来弥补财政赤字
当政府停止这种政策后，持续通货膨胀将消退

本讲座使用的是菲利普·凯根[Cagan, 1956]恶性通货膨胀模型的”理性预期”（或”完全预见”）版本。虽然凯根本人没有使用理性预期版本，但托马斯·萨金特[Sargent, 1982]在研究一战后欧洲四大通货膨胀的终结时采用了这一版本。

在讲座基于适应性预期的价格水平财政理论中，我们介绍了一个使用”适应性预期”（凯根和其导师米尔顿·弗里德曼提出的概念）而非”理性预期”的模型版本
- 值得注意的是，理性预期版本的代数相对简单
- 适应性预期版本更复杂的原因在于它包含更多内生变量和自由参数

我们将通过一系列定量实验，展示这个财政理论如何解释那些大通货膨胀的突然终结。在这些实验中，我们会观察到”速度红利”现象——这种现象常见于成功的通货膨胀稳定计划中。

为了便于使用线性矩阵代数作为主要数学工具，我们将采用该模型的有限时间版本。与现值和消费平滑讲座类似，我们主要运用矩阵乘法和矩阵求逆这些数学工具。

14.2. 模型结构#

该模型包括

一个函数，表示实际货币余额需求是预期通货膨胀率的反函数
外生的货币供应增长率序列。货币供应增长是因为政府印钞来支付商品和服务
使货币需求等于供给的均衡条件

这个模型假设公众”完全预见”实际通胀率，即公众预期的通货膨胀率等于实际通货膨胀率

为了正式表示该模型，令

$ m_t $ 为名义货币余额供应的对数
$\mu_t = m_{t+1} - m_t $ 为名义余额的净增长率
$p_t $ 为价格水平的对数
$\pi_t = p_{t+1} - p_t $ 为 $t$ 和 $ t+1$ 之间的净通货膨胀率
$\pi_t^*$ 为公众预期的时刻 $t$ 和 $t+1$ 之间的通货膨胀率
$T$ 为时间范围 – 即模型将确定 $p_t$ 的最后一个时期
$\pi_{T+1}^*$ 为 $T$ 和 $T+1$ 之间的终端通货膨胀率

实际余额 $\exp\left(m_t^d - p_t\right)$ 的需求由以下版本的凯根需求函数决定

(14.1)#\[ m_t^d - p_t = -\alpha \pi_t^* \: , \: \alpha > 0 ; \quad t = 0, 1, \ldots, T . \]

这个方程表明，实际货币余额的需求与预期通货膨胀率成反比。

人们通过解决预测问题获得了完全预见。

这让我们设置

(14.2)#\[ \pi_t^* = \pi_t , \forall t \]

同时使货币需求等于供给让我们对所有 $t \geq 0$ 设置 $m_t^d = m_t$。

前面的方程然后意味着

(14.3)#\[ m_t - p_t = -\alpha(p_{t+1} - p_t) \]

为了使个体完全预见通胀率,我们从时间 $ t $ 的方程 (14.3) 中减去 $ t+1 $ 时的相同方程得到

\[ \mu_t - \pi_t = -\alpha \pi_{t+1} + \alpha \pi_t , \]

我们将其重写为关于 $\pi_s$ 的前瞻性一阶线性差分方程,其中 $\mu_s$ 作为”强制变量”:

\[ \pi_t = \frac{\alpha}{1+\alpha} \pi_{t+1} + \frac{1}{1+\alpha} \mu_t , \quad t= 0, 1, \ldots , T \]

其中 $ 0< \frac{\alpha}{1+\alpha} <1$。

设 $\delta =\frac{\alpha}{1+\alpha}$,让我们将前面的方程表示为

\[ \pi_t = \delta \pi_{t+1} + (1-\delta) \mu_t , \quad t =0, 1, \ldots, T \]

将这个 $T+1$ 个方程的系统写成单个矩阵方程

(14.4)#\[ \begin{bmatrix} 1 & -\delta & 0 & 0 & \cdots & 0 & 0 \cr 0 & 1 & -\delta & 0 & \cdots & 0 & 0 \cr 0 & 0 & 1 & -\delta & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & -\delta & 0 \cr 0 & 0 & 0 & 0 & \cdots & 1 & -\delta \cr 0 & 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \begin{bmatrix} \pi_0 \cr \pi_1 \cr \pi_2 \cr \vdots \cr \pi_{T-1} \cr \pi_T \end{bmatrix} = (1 - \delta) \begin{bmatrix} \mu_0 \cr \mu_1 \cr \mu_2 \cr \vdots \cr \mu_{T-1} \cr \mu_T \end{bmatrix} + \begin{bmatrix} 0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr \delta \pi_{T+1}^* \end{bmatrix} \]

通过将方程 (14.4) 两边乘以左侧矩阵的逆,我们可以计算

\[ \pi \equiv \begin{bmatrix} \pi_0 \cr \pi_1 \cr \pi_2 \cr \vdots \cr \pi_{T-1} \cr \pi_T \end{bmatrix} \]

结果是

(14.5)#\[ \pi_t = (1-\delta) \sum_{s=t}^T \delta^{s-t} \mu_s + \delta^{T+1-t} \pi_{T+1}^* \]

我们可以将方程

\[ m_{t+1} = m_t + \mu_t , \quad t = 0, 1, \ldots, T \]

表示为矩阵方程

(14.6)#\[ \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 & 0 \cr -1 & 1 & 0 & \cdots & 0 & 0 \cr 0 & -1 & 1 & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & 0 & 0 \cr 0 & 0 & 0 & \cdots & 1 & 0 \cr 0 & 0 & 0 & \cdots & -1 & 1 \end{bmatrix} \begin{bmatrix} m_1 \cr m_2 \cr m_3 \cr \vdots \cr m_T \cr m_{T+1} \end{bmatrix} = \begin{bmatrix} \mu_0 \cr \mu_1 \cr \mu_2 \cr \vdots \cr \mu_{T-1} \cr \mu_T \end{bmatrix} + \begin{bmatrix} m_0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr 0 \end{bmatrix} \]

将方程 (14.6) 两边乘以左侧矩阵的逆将得到

(14.7)#\[ m_t = m_0 + \sum_{s=0}^{t-1} \mu_s, \quad t =1, \ldots, T+1 \]

方程 (14.7) 显示，时间 $t$ 的货币供应对数等于初始货币供应对数 $m_0$ 加上从时间 $0$ 到 $T$ 之间的货币增长率累积。

14.3. 延续值#

为确定延续通胀率 $\pi_{T+1}^*$，我们将在 $t = T+1$ 时应用以下方程 (14.5) 的无限期版本：

(14.8)#\[ \pi_t = (1-\delta) \sum_{s=t}^\infty \delta^{s-t} \mu_s , \]

并假设 $T$ 之后 $\mu_t$ 的延续路径如下：

\[ \mu_{t+1} = \gamma^* \mu_t, \quad t \geq T . \]

将上述方程代入 $t = T+1$ 时的方程 (14.8) 并重新排列，我们可以推导出：

(14.9)#\[ \pi_{T+1}^* = \frac{1 - \delta}{1 - \delta \gamma^*} \gamma^* \mu_T \]

其中我们要求 $\vert \gamma^* \delta \vert < 1$。

让我们实现并解决这个模型。

像往常一样，我们将从导入一些 Python 模块开始。

import numpy as np
from collections import namedtuple
import matplotlib.pyplot as plt
plt.rcParams['figure.dpi'] = 200

import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

首先，我们将参数存储在一个namedtuple中：

# "创建有限视界凯根模型的理性预期版本"
CaganREE = namedtuple("CaganREE", 
                        ["m0",    # 初始货币供给
                         "μ_seq", # 增长率序列
                         "α",     # 敏感度参数
                         "δ",     # α/(1 + α)
                         "π_end"  # 最后一期的预期通货膨胀率
                        ])

def create_cagan_model(m0=1, α=5, μ_seq=None):
    δ = α/(1 + α)
    π_end = μ_seq[-1]    # 计算最后一期的预期通货膨胀率
    return CaganREE(m0, μ_seq, α, δ, π_end)

现在我们可以求解这个模型通过矩阵方程来计算$\pi_t$, $m_t$ 和 $p_t$ 当 $t =1, \ldots, T+1$

def solve(model, T):
    m0, π_end, μ_seq, α, δ = (model.m0, model.π_end, 
                              model.μ_seq, model.α, model.δ)
    
    # 创建矩阵
    A1 = np.eye(T+1, T+1) - δ * np.eye(T+1, T+1, k=1)
    A2 = np.eye(T+1, T+1) - np.eye(T+1, T+1, k=-1)

    b1 = (1-δ) * μ_seq + np.concatenate([np.zeros(T), [δ * π_end]])
    b2 = μ_seq + np.concatenate([[m0], np.zeros(T)])

    π_seq = np.linalg.solve(A1, b1)
    m_seq = np.linalg.solve(A2, b2)

    π_seq = np.append(π_seq, π_end)
    m_seq = np.append(m0, m_seq)

    p_seq = m_seq + α * π_seq

    return π_seq, m_seq, p_seq

14.3.1. 一些定量实验#

在接下来的实验中，我们会用公式 (14.9) 来确定预期通货膨胀的终值。我们会设计一系列实验，其中货币增长率序列 $\{\mu_t\}$ 都满足公式 (14.9) 中的条件。让我们一起看看这些实验。

在所有这些实验中，

\[ \mu_t = \mu^* , \quad t \geq T_1 \]

根据上述符号和 $\pi_{T+1}^*$ 的计算公式，我们可以得到 $\tilde \gamma = 1$。

14.3.1.1. 实验1：可预期的突然稳定#

在这个实验中，我们将探讨当 $\alpha >0$ 时，一个可预期的通货膨胀稳定政策会如何影响其实施前的通货膨胀走势。具体来说，我们将分析这样一种情况：货币供应增长率在 $t=0$ 到 $t=T_1$ 期间保持在 $\mu_0$ 的水平，然后在 $t=T_1$ 时刻突然永久性地降至 $\mu^*$。

因此，令 $T_1 \in (0, T)$。

所以当 $\mu_0 > \mu^*$ 时，我们假设

\[\begin{split} \mu_{t+1} = \begin{cases} \mu_0 , & t = 0, \ldots, T_1 -1 \\ \mu^* , & t \geq T_1 \end{cases} \end{split}\]

让我们先来看”实验1”，在这个实验中，政府会在时间 $T_1$ 实施一个可预见的政策使货币供应增长率的突然永久性下调。

我们设定以下参数来进行实验

T1 = 60
μ0 = 0.5
μ_star = 0
T = 80

μ_seq_1 = np.append(μ0*np.ones(T1+1), μ_star*np.ones(T-T1))

cm = create_cagan_model(μ_seq=μ_seq_1)

# 求解模型
π_seq_1, m_seq_1, p_seq_1 = solve(cm, T)

我们用下面的函数来进行绘图

def plot_sequences(sequences, labels):
    fig, axs = plt.subplots(len(sequences), 1, figsize=(5, 12))
    for ax, seq, label in zip(axs, sequences, labels):
        ax.plot(range(len(seq)), seq, label=label)
        ax.set_ylabel(label)
        ax.set_xlabel('$t$')
        ax.legend()
    plt.tight_layout()
    plt.show()

sequences = (μ_seq_1, π_seq_1, m_seq_1 - p_seq_1, m_seq_1, p_seq_1)
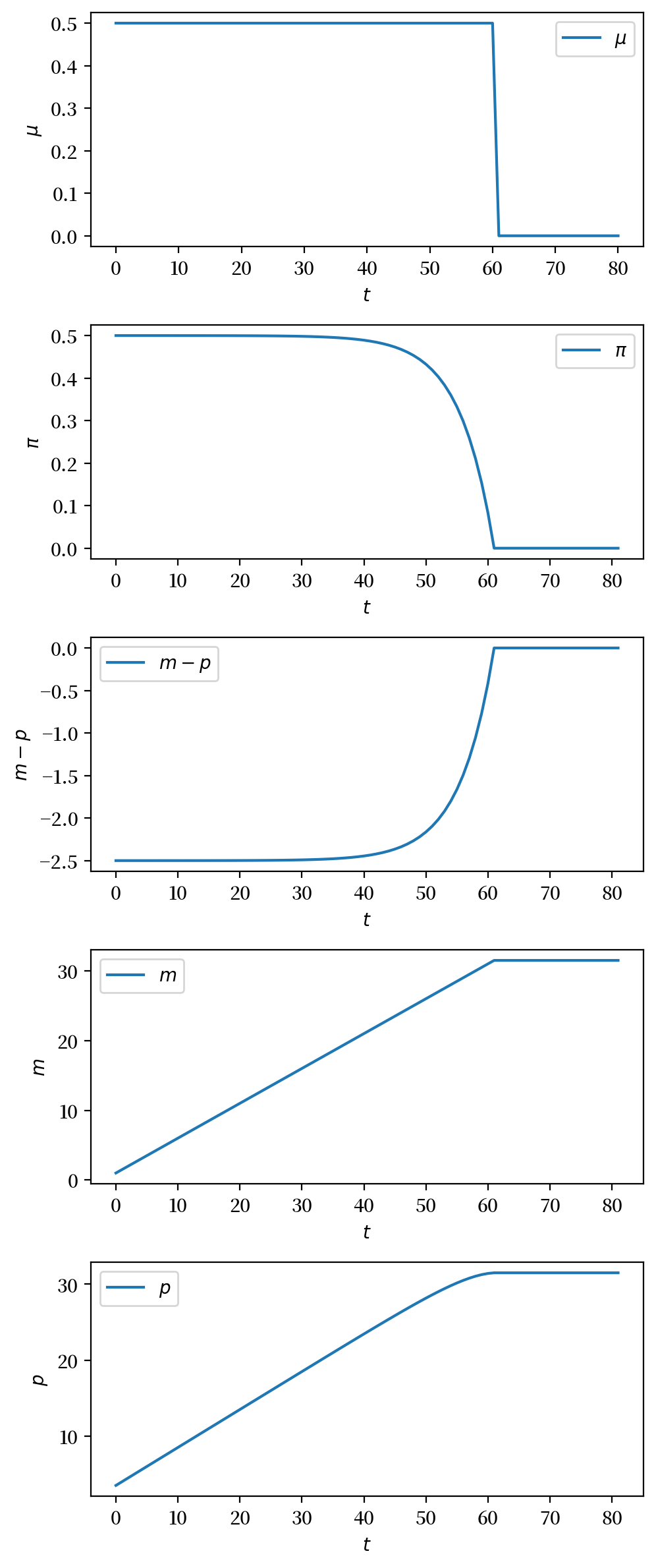
plot_sequences(sequences, (r'$\mu$', r'$\pi$', r'$m - p$', r'$m$', r'$p$'))

_images/7dee911192182b83d188b95968dc26768dae912cb959c6e98c4a755dd89d1b60.png

顶部面板中货币增长率 $\mu_t$ 的图表显示在时间 $T_1 = 60$ 时从 $.5$ 突然降至 $0$。

这导致通货膨胀率 $\pi_t$ 在 $T_1$ 之前逐渐降低。

注意通货膨胀率如何平滑（即连续）地降至 $T_1$ 时的 $0$ —— 与货币增长率不同，它在 $T_1$ 时并没有突然”跳跃”下降。

这是因为经济主体从一开始就预见到了在 $T_1$ 时货币增长率 $\mu$ 会下降。

从底部面板可以看到，虽然对数货币供应在 $T_1$ 处出现了明显的拐点，但对数价格水平却保持平滑变化。这也是因为经济主体提前预见到了货币增长率的下降。

在进行下一个实验之前，我们需要更深入地理解价格水平是如何决定的。

14.3.2. 对数价格水平#

根据方程 (14.1) 和 (14.2)，我们可以推导出对数价格水平满足以下关系：

(14.10)#\[ p_t = m_t + \alpha \pi_t \]

或者，通过方程(14.5)我们可以推导

(14.11)#\[ p_t = m_t + \alpha \left[ (1-\delta) \sum_{s=t}^T \delta^{s-t} \mu_s + \delta^{T+1-t} \pi_{T+1}^* \right] \]

在下一个实验中，我们将探讨一个”意外”的永久性货币增长变化。这种变化是完全出乎意料的,事先没有任何预期。

当这种”意外”的货币增长率变化在时间 $T_1$ 发生时,为了满足公式 (14.10),实际货币余额的对数会随着通货膨胀率 $\pi_t$ 的下降而上升。

但要实现实际货币余额 $m_t - p_t$ 的跳跃,究竟是货币供应量 $m_{T_1}$ 还是价格水平 $p_{T_1}$ 需要跳跃呢？

这是一个值得深入探讨的问题。

14.3.3. 跳跃的变量#

在时间点 $T_1$,到底是什么变量发生了跳跃？

是价格水平 $p_{T_1}$ 还是货币供应量 $m_{T_1}$ 呢？

如果我们假定货币供应量 $m_{T_1}$ 固定在从过去继承的水平 $m_{T_1}^1$，那么根据公式 (14.10)，价格水平必须在 $T_1$ 时向下跳跃，以适应 $\pi_{T_1}$ 的下降。

另一种可能的假设是，作为”通货膨胀稳定计划”的一部分，政府会按照以下公式调整货币供应量 $m_{T_1}$：

(14.12)#\[ m_{T_1}^2 - m_{T_1}^1 = \alpha (\pi_{T_1}^1 - \pi_{T_1}^2), \]

这个公式描述了政府如何在 $T_1$ 时调整货币供应量，以应对稳定计划带来的预期通货膨胀率的变化。

这样做可以使价格水平在 $T_1$ 时保持连续。

通过按照公式 (14.12) 调整货币供应量，货币当局避免了在实施稳定计划时价格水平的下跌。

在研究高通胀稳定的文献中，公式 (14.12) 描述的货币供应量调整被称为”速度红利”——这是政府通过实施长期低通胀制度而获得的好处。

14.3.3.1. 关于价格水平 $p$ 还是货币供应量 $m$ 在 $T_1$ 时的跳跃#

我们注意到，当 $s\geq t$ 时如果预期的未来货币增长率序列 $\mu_s$ 保持在常数水平 $\bar \mu$，那么通胀率 $\pi_{t}$ 也会等于 $\bar{\mu}$。

这意味着在 $T_1$ 时，$m$ 或 $p$ 必须有一个”跳跃”。

让我们分析这两种情况。

14.3.3.2. 情况一：$m_{T_{1}}$ 不跳跃#

\[\begin{split} \begin{aligned} m_{T_{1}}&=m_{T_{1}-1}+\mu_{0}\\\pi_{T_{1}}&=\mu^{*}\\p_{T_{1}}&=m_{T_{1}}+\alpha\pi_{T_{1}} \end{aligned} \end{split}\]

我们只需将 $t\leq T_1$ 和 $t > T_1$ 的序列直接连接起来。

14.3.3.3. 情况二：$m_{T_{1}}$ 跳跃#

我们调整 $m_{T_{1}}$ 使得 $p_{T_{1}}=\left(m_{T_{1}-1}+\mu_{0}\right)+\alpha\mu_{0}$，同时 $\pi_{T_{1}}=\mu^{*}$。

因此，

\[ m_{T_{1}}=p_{T_{1}}-\alpha\pi_{T_{1}}=\left(m_{T_{1}-1}+\mu_{0}\right)+\alpha\left(\mu_{0}-\mu^{*}\right) \]

然后我们计算剩余的 $T-T_{1}$ 期，其中 $\mu_{s}=\mu^{*},\forall s\geq T_{1}$，并使用上述 $m_{T_{1}}$ 作为初始条件。

有了这些技术准备，我们现在可以进行下一个实验了。

14.3.3.4. 实验2：不可预期的突然稳定#

这个实验稍微偏离了我们之前的”完全预见”假设。我们假设货币增长率 $\mu_t$ 的突然永久性下降是完全出乎意料的,而不像实验1那样是可预见的。

这种完全出乎意料的冲击在经济学中通常被称为”MIT冲击”。

这个思想实验涉及在时间 $T_1$ 从一个初始路径切换到另一个低通胀率的路径。

初始路径： 所有时期 $t \geq 0$ 的货币增长率都是 $\mu_t = \mu_0$。因此这个路径是 $\{\mu_t\}_{t=0}^\infty$；对应的通胀率路径是 $\pi_t = \mu_0$。

修正后的路径： 当 $\mu_0 > \mu^*$ 时，我们构建一个新路径 $\{\mu_s\}_{s=T_1}^\infty$，其中所有 $s \geq T_1$ 时期的货币增长率都是 $\mu_s = \mu^*$。在完全预见下，对应的通胀率路径是 $\pi_s = \mu^*$。

为了模拟在时间 $T_1$ 对货币增长率 $\{\mu_t\}$ 的”完全不可预期的永久性冲击”，我们只需将两段路径拼接起来：

$t < T_1$ 时采用初始路径的 $\mu_t$ 和 $\pi_t$
$t \geq T_1$ 时采用修正后路径的 $\mu_t$ 和 $\pi_t$

这个MIT冲击的计算相对直观：

在路径1中，$t \in [0, T_1-1]$ 时期的通胀率是 $\pi_t = \mu_0$
在路径2中，$s \geq T_1$ 时期的货币增长率是 $\mu_s = \mu^*$

具体来说，在路径1中，通货膨胀率 $\pi_t$ 在时间区间 $[0, T_1-1]$ 内保持在 $\mu_0$ 的水平。而在路径2中，从 $T_1$ 时刻开始，货币增长率 $\mu_s$ 永久性地降至 $\mu^*$ 的水平。

接下来我们将进行实验2，即研究一个完全出乎意料的突然稳定政策的”MIT冲击”的效果。

为了便于比较，我们将使用与实验1（可预期的突然稳定）相同的货币增长率序列 $\{\mu_t\}$。这样可以清晰地看出两种情况下经济变量的不同表现。

以下代码进行计算并绘制结果。

# 路径 1
μ_seq_2_path1 = μ0 * np.ones(T+1)

cm1 = create_cagan_model(μ_seq=μ_seq_2_path1)
π_seq_2_path1, m_seq_2_path1, p_seq_2_path1 = solve(cm1, T)

# 继续路径
μ_seq_2_cont = μ_star * np.ones(T-T1)

cm2 = create_cagan_model(m0=m_seq_2_path1[T1+1], 
                         μ_seq=μ_seq_2_cont)
π_seq_2_cont, m_seq_2_cont1, p_seq_2_cont1 = solve(cm2, T-1-T1)


# 方案1 - 简单粘合 π_seq, μ_seq
μ_seq_2 = np.concatenate((μ_seq_2_path1[:T1+1],
                          μ_seq_2_cont))
π_seq_2 = np.concatenate((π_seq_2_path1[:T1+1], 
                          π_seq_2_cont))
m_seq_2_regime1 = np.concatenate((m_seq_2_path1[:T1+1], 
                                  m_seq_2_cont1))
p_seq_2_regime1 = np.concatenate((p_seq_2_path1[:T1+1], 
                                  p_seq_2_cont1))

# 方案 2 - 重制 m_T1
m_T1 = (m_seq_2_path1[T1] + μ0) + cm2.α*(μ0 - μ_star)

cm3 = create_cagan_model(m0=m_T1, μ_seq=μ_seq_2_cont)
π_seq_2_cont2, m_seq_2_cont2, p_seq_2_cont2 = solve(cm3, T-1-T1)

m_seq_2_regime2 = np.concatenate((m_seq_2_path1[:T1+1], 
                                  m_seq_2_cont2))
p_seq_2_regime2 = np.concatenate((p_seq_2_path1[:T1+1],
                                  p_seq_2_cont2))

_images/97b8d74761d8f6a0ab7b4cc9ff2dd5ade001270a4dcc0811905c8ed029741031.png

让我们将这些图表与实验1中的预期稳定化图表进行对比。

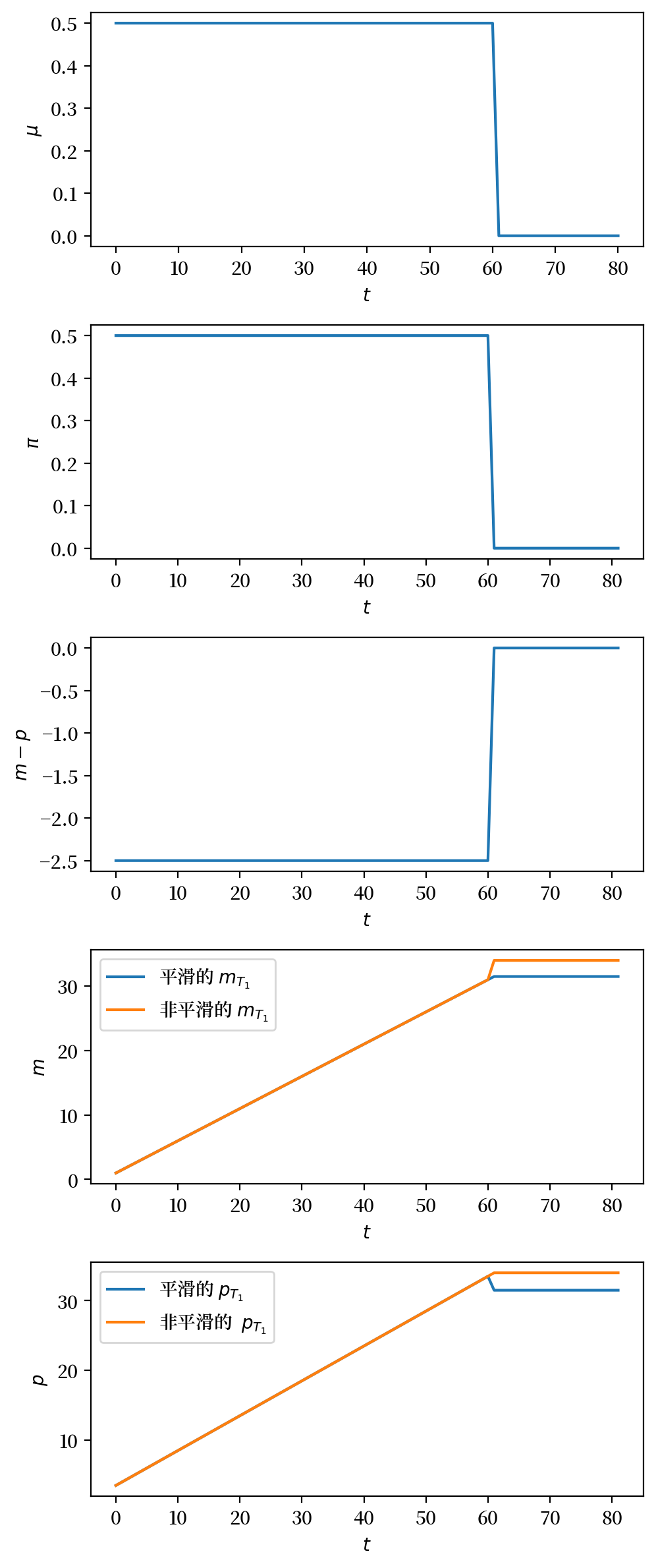
从图中可以看到几个有趣的现象:

第二副图中的通货膨胀率完全跟随了顶部面板中的货币增长率变化。同时，第三副图显示实际货币余额(以对数表示)在时间$T_1$处出现了向上跳跃。

底部两副图展示了$m_{T_1}$在满足$m - p$向上跳跃要求时可能的两种调整方式:

橙色线显示了$m_{T_1}$向上跳跃的情况,这确保了价格水平$p_{T_1}$不会下降
蓝色线则显示了让$p_{T_1}$下降而保持货币供应量平稳的情况

橙色线代表的政策可以这样理解:政府通过增发货币来支付支出,同时利用货币供应增长率永久下降带来的实际余额需求增加所产生的”速度红利”。

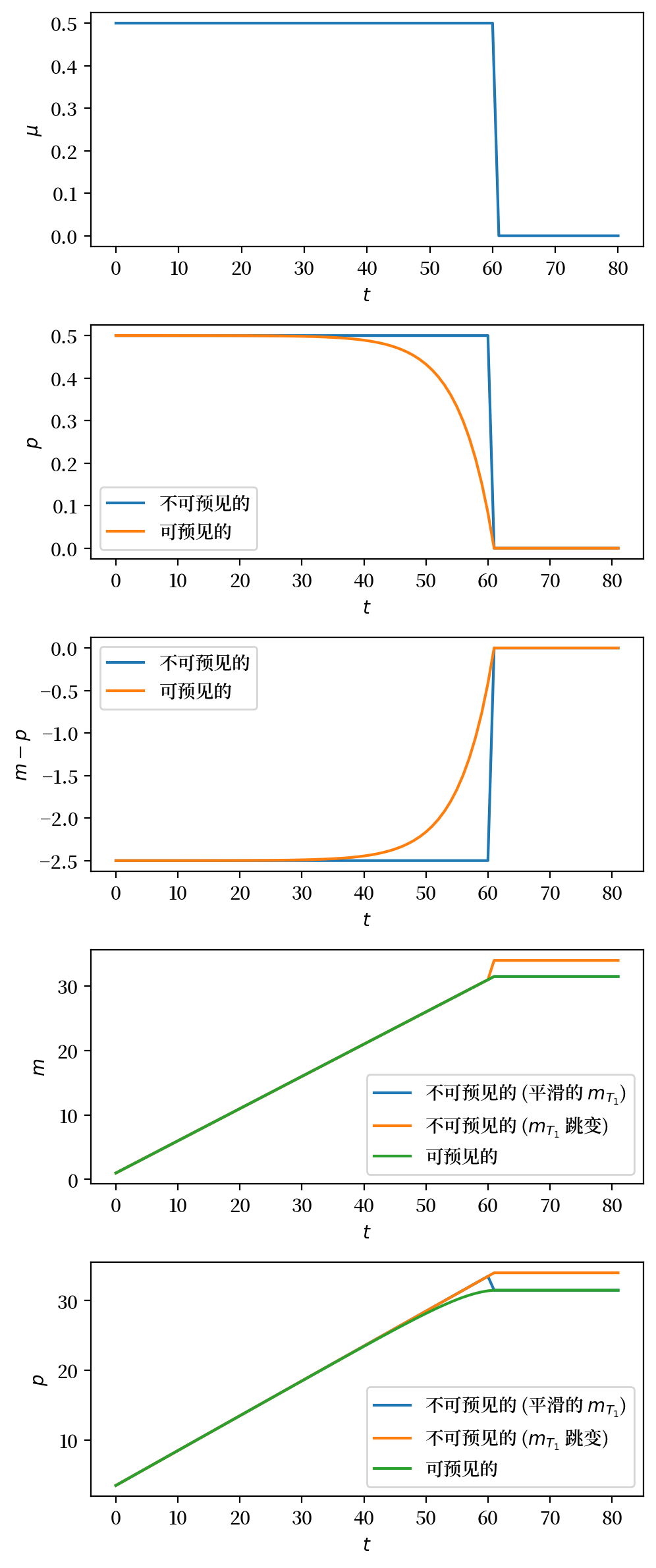
下面的代码将生成一个多面板图,把实验1和实验2的结果放在一起比较。

这让我们能够清楚地看到:当$\mu_t$在$t=T_1$时突然永久下降时,这种变化是完全可预期的(如实验1)还是完全出乎意料的(如实验2)会带来怎样的差异。

_images/873b49c2dd362732209e5cddf8ac823cffa98bf5c85070b3907b3a153d9a82a1.png

将上图与这篇讲座中描述的四次大通货膨胀的数据进行对比很有启发性。我们可以比较它们的价格水平对数和通货膨胀率走势。

从上面的图表中我们可以观察到一个有趣的现象:当通货膨胀稳定是可预见的时候,通货膨胀率会在”突然停止”之前就开始逐渐下降。相反,如果货币供应增长的永久性下降是出乎意料的,通货膨胀率会突然下降。

通过对比这篇讲座中描述的四次恶性通货膨胀的结尾阶段,quantecon的作者团队认为它们的通货膨胀率走势更接近实验2中”不可预见的稳定”的情况。

(当然,这种非正式的模式识别还需要更严谨的结构统计分析来支持。)

14.3.3.5. 实验3#

可预见的渐进稳定

除了研究实验1中那种突然稳定的情况,我们也来看看当稳定过程是渐进的、可预见的时候会发生什么。

具体来说,假设$\phi \in (0,1)$,$\mu_0 > \mu^*$,且货币增长率按以下方式演变: $$ \mu_t = \phi^t \mu_0 + (1 - \phi^t) \mu^* . $$

接下来，我们进行一个实验，其中货币供应增长率会完全可预见地逐渐下降。

以下代码进行计算并绘制结果。

# 参数
ϕ = 0.9
μ_seq_stab = np.array([ϕ**t * μ0 + (1-ϕ**t)*μ_star for t in range(T)])
μ_seq_stab = np.append(μ_seq_stab, μ_star)

cm4 = create_cagan_model(μ_seq=μ_seq_stab)

π_seq_4, m_seq_4, p_seq_4 = solve(cm4, T)

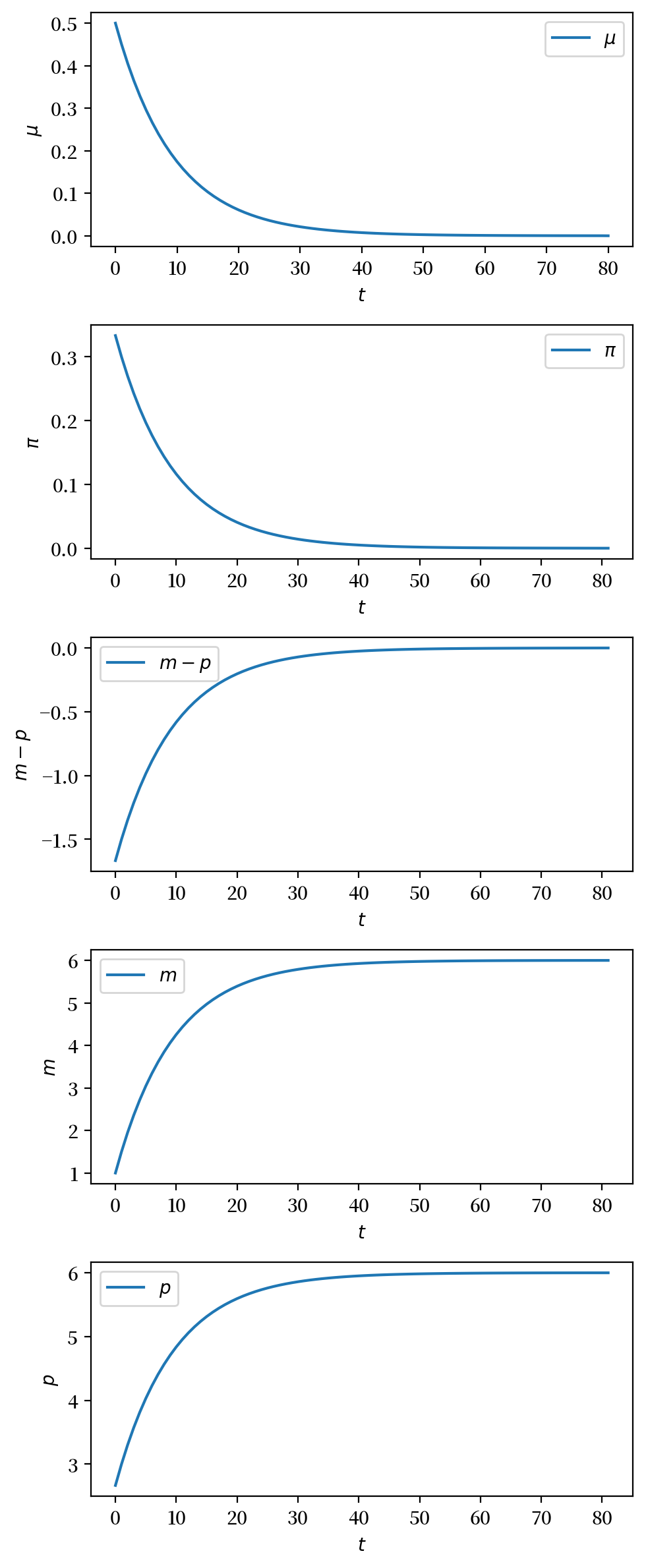
sequences = (μ_seq_stab, π_seq_4, 
             m_seq_4 - p_seq_4, m_seq_4, p_seq_4)
plot_sequences(sequences, (r'$\mu$', r'$\pi$', 
                           r'$m - p$', r'$m$', r'$p$'))

_images/d81e38611fb3d3451539b792f8a4a0b47b405940ffbed2ddcfff1685d307ff4b.png

14.4. 续篇#

在带有适应性预期的价格水平货币主义理论中，我们将介绍凯根模型的”适应性预期”版本。

虽然适应性预期版本的动态和代数运算更为复杂，但它帮助我们理解了人们如何逐步调整他们的通胀预期。

如今，由于理性预期版本能更好地解释现代经济中的通胀动态，它在当今的中央银行和经济学界更受青睐。