37. 最短路径#

37.1. 概述#

最短路径问题是数学和计算机科学中的一个经典问题，其应用包括：

经济学（顺序决策、社会网络分析等）
运筹学和交通运输
机器人技术和人工智能
电信网络设计和路由
等等

我们在本讲座中讨论的方法的变体每天在许多应用中使用数百万次，例如：

谷歌地图
互联网数据包路由

对于我们来说，最短路径问题也为动态规划的逻辑提供了一个很好的介绍。

动态规划是一种非常强大的优化技术，我们在本网站的许多讲座中都会应用它。

接下来我们唯一需要的科学库是NumPy：

import numpy as np

37.2. 问题概述#

最短路径问题是寻找如何以最小成本从图中的一个指定节点遍历到另一个节点。考虑下面这个图

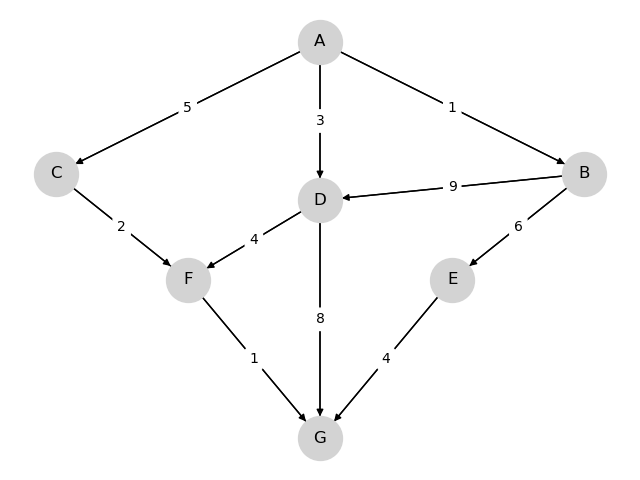
我们希望以最小成本从节点（顶点）A到达节点G

箭头（边）表示我们可以采取的移动。
边上的数字表示沿该边行进的成本。（像上面这样的图被称为加权有向图。）图的可能解释包括
供应商到达目的地的最小成本。
互联网上的数据包路由（最小化时间）。
等等。对于这个简单的图，快速扫描边可以看出最优路径是
A, C, F, G，成本为8

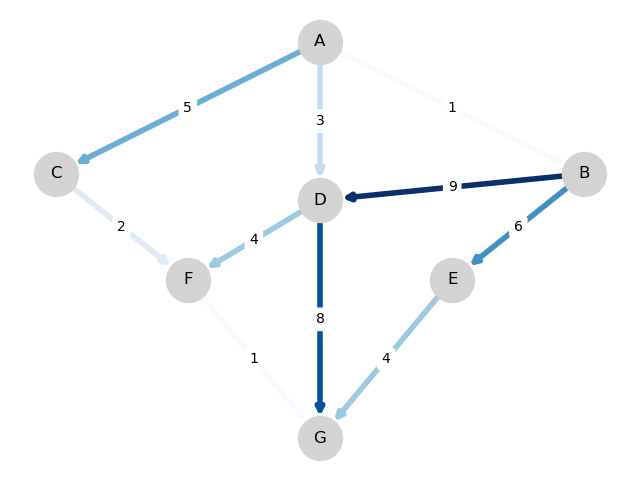
A, D, F, G，成本为8

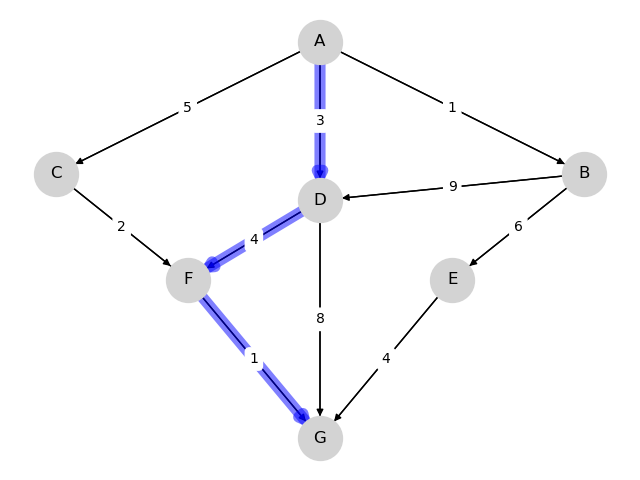
37.3. 寻找最低成本路径#

对于大型图，我们需要一个系统的解决方案。让 \(J(v)\) 表示从节点 \(v\) 出发的最小成本，理解为如果我们选择最佳路线，从 \(v\) 出发的总成本。假设我们知道每个节点 \(v\) 的 \(J(v)\)，如下图所示（基于前面示例中的图）。

注意 \(J(G) = 0\)。现在可以通过以下步骤找到最佳路径：

从节点 \(v = A\) 开始
从当前节点 \(v\)，移动到解决以下问题的任何节点

(37.1)#\[\min_{w \in F_v} \{ c(v, w) + J(w) \}\]

其中

\(F_v\) 是可以从 \(v\) 一步到达的节点集合。
\(c(v, w)\) 是从 \(v\) 到 \(w\) 的旅行成本。因此，如果我们知道函数 \(J\)，那么找到最佳路径几乎就是微不足道的事。但是我们如何找到成本函数 \(J\) 呢？经过一些思考，你会确信对于每个节点 \(v\)，函数 \(J\) 满足

(37.2)#\[J(v) = \min_{w \in F_v} \{ c(v, w) + J(w) \}\]

这被称为贝尔曼方程，以数学家理查德·贝尔曼的名字命名。

贝尔曼方程可以被理解为\(J\)必须满足的一个限制条件。

我们现在想要做的是利用这个限制条件来计算\(J\)。

37.4. 求解最小代价-到-目标#

让我们来看一个计算\(J\)的算法，然后思考如何实现它。

37.4.1. 算法#

找到\(J\)的标准算法是从一个初始猜测开始，然后进行迭代。

这是解决非线性方程的标准方法，通常被称为连续近似法。

我们的初始猜测将是

(37.3)#\[J_0(v) = 0 \text{ for all } v\]

现在

设 \(n = 0\)
对所有 \(v\)，设 \(J_{n+1} (v) = \min_{w \in F_v} \{ c(v, w) + J_n(w) \}\)
如果 \(J_{n+1}\) 和 \(J_n\) 不相等，则将 \(n\) 加 1，返回步骤 2 这个序列收敛于 \(J\)。虽然我们在此省略了证明，但我们将在其他动态规划讲座中证明类似的结论。

37.4.2. 实现#

有了算法是一个好的开始，但我们还需要考虑如何在计算机上实现它。

首先，对于成本函数 \(c\)，我们将其实现为矩阵 \(Q\)，其中典型元素为

\[\begin{split} Q(v, w) = \begin{cases} & c(v, w) \text{ 如果 } w \in F_v \\ & +\infty \text{ 否则 } \end{cases} \end{split}\]

在这种情况下，\(Q\) 通常被称为距离矩阵。

我们现在也对节点进行编号，其中 \(A = 0\)，所以，例如

\[ Q(1, 2) = \text{ 从 B 到 C 的旅行成本 } \]

例如，对于上面的简单图，我们设置

from numpy import inf

Q = np.array([[inf, 1,   5,   3,   inf, inf, inf],
              [inf, inf, inf, 9,   6,   inf, inf],
              [inf, inf, inf, inf, inf, 2,   inf],
              [inf, inf, inf, inf, inf, 4,   8],
              [inf, inf, inf, inf, inf, inf, 4],
              [inf, inf, inf, inf, inf, inf, 1],
              [inf, inf, inf, inf, inf, inf, 0]])

请注意，保持不动（在主对角线上）的成本设置为：

对于非目的地节点，设为 np.inf — 必须继续移动。
对于目的地节点，设为 0 — 这是我们停止的地方。对于到达成本函数的近似序列 \(\{J_n\}\)，我们可以使用 NumPy 数组。让我们尝试这个例子，看看效果如何：

nodes = range(7)                              # 节点 = 0, 1, ..., 6
J = np.zeros_like(nodes, dtype=int)        # 初始猜测
next_J = np.empty_like(nodes, dtype=int)   # 储存更新的猜测

max_iter = 500
i = 0

while i < max_iter:
    for v in nodes:
        # 最小化所有 w 选择中的 Q[v, w] + J[w]
        next_J[v] = np.min(Q[v, :] + J)
    
    if np.array_equal(next_J, J):                
        break
    
    J[:] = next_J                                # 将 next_J 的内容复制到 J
    i += 1

print("到达成本函数是", J)

到达成本函数是 [ 8 10  3  5  4  1  0]

这与我们上面通过观察得到的数字相符。但更重要的是，我们现在有了一种处理大型图的方法。

37.5. 练习#

Exercise 37.1

以下文本描述了一个加权有向图。

行 node0, node1 0.04, node8 11.11, node14 72.21 表示从node0我们可以到达：

node1，代价为0.04
node8，代价为11.11
node14，代价为72.21 从node0无法直接到达其他节点。其他行具有类似的解释。你的任务是使用上面给出的算法来找到最优路径及其代价。

Note

现在你将处理浮点数而不是整数，所以考虑用 np.allclose() 替换 np.equal()。

%%file graph.txt
node0, node1 0.04, node8 11.11, node14 72.21
node1, node46 1247.25, node6 20.59, node13 64.94
node2, node66 54.18, node31 166.80, node45 1561.45
node3, node20 133.65, node6 2.06, node11 42.43
node4, node75 3706.67, node5 0.73, node7 1.02
node5, node45 1382.97, node7 3.33, node11 34.54
node6, node31 63.17, node9 0.72, node10 13.10
node7, node50 478.14, node9 3.15, node10 5.85
node8, node69 577.91, node11 7.45, node12 3.18
node9, node70 2454.28, node13 4.42, node20 16.53
node10, node89 5352.79, node12 1.87, node16 25.16
node11, node94 4961.32, node18 37.55, node20 65.08
node12, node84 3914.62, node24 34.32, node28 170.04
node13, node60 2135.95, node38 236.33, node40 475.33
node14, node67 1878.96, node16 2.70, node24 38.65
node15, node91 3597.11, node17 1.01, node18 2.57
node16, node36 392.92, node19 3.49, node38 278.71
node17, node76 783.29, node22 24.78, node23 26.45
node18, node91 3363.17, node23 16.23, node28 55.84
node19, node26 20.09, node20 0.24, node28 70.54
node20, node98 3523.33, node24 9.81, node33 145.80
node21, node56 626.04, node28 36.65, node31 27.06
node22, node72 1447.22, node39 136.32, node40 124.22
node23, node52 336.73, node26 2.66, node33 22.37
node24, node66 875.19, node26 1.80, node28 14.25
node25, node70 1343.63, node32 36.58, node35 45.55
node26, node47 135.78, node27 0.01, node42 122.00
node27, node65 480.55, node35 48.10, node43 246.24
node28, node82 2538.18, node34 21.79, node36 15.52
node29, node64 635.52, node32 4.22, node33 12.61
node30, node98 2616.03, node33 5.61, node35 13.95
node31, node98 3350.98, node36 20.44, node44 125.88
node32, node97 2613.92, node34 3.33, node35 1.46
node33, node81 1854.73, node41 3.23, node47 111.54
node34, node73 1075.38, node42 51.52, node48 129.45
node35, node52 17.57, node41 2.09, node50 78.81
node36, node71 1171.60, node54 101.08, node57 260.46
node37, node75 269.97, node38 0.36, node46 80.49
node38, node93 2767.85, node40 1.79, node42 8.78
node39, node50 39.88, node40 0.95, node41 1.34
node40, node75 548.68, node47 28.57, node54 53.46
node41, node53 18.23, node46 0.28, node54 162.24
node42, node59 141.86, node47 10.08, node72 437.49
node43, node98 2984.83, node54 95.06, node60 116.23
node44, node91 807.39, node46 1.56, node47 2.14
node45, node58 79.93, node47 3.68, node49 15.51
node46, node52 22.68, node57 27.50, node67 65.48
node47, node50 2.82, node56 49.31, node61 172.64
node48, node99 2564.12, node59 34.52, node60 66.44
node49, node78 53.79, node50 0.51, node56 10.89
node50, node85 251.76, node53 1.38, node55 20.10
node51, node98 2110.67, node59 23.67, node60 73.79
node52, node94 1471.80, node64 102.41, node66 123.03
node53, node72 22.85, node56 4.33, node67 88.35
node54, node88 967.59, node59 24.30, node73 238.61
node55, node84 86.09, node57 2.13, node64 60.80
node56, node76 197.03, node57 0.02, node61 11.06
node57, node86 701.09, node58 0.46, node60 7.01
node58, node83 556.70, node64 29.85, node65 34.32
node59, node90 820.66, node60 0.72, node71 0.67
node60, node76 48.03, node65 4.76, node67 1.63
node61, node98 1057.59, node63 0.95, node64 4.88
node62, node91 132.23, node64 2.94, node76 38.43
node63, node66 4.43, node72 70.08, node75 56.34
node64, node80 47.73, node65 0.30, node76 11.98
node65, node94 594.93, node66 0.64, node73 33.23
node66, node98 395.63, node68 2.66, node73 37.53
node67, node82 153.53, node68 0.09, node70 0.98
node68, node94 232.10, node70 3.35, node71 1.66
node69, node99 247.80, node70 0.06, node73 8.99
node70, node76 27.18, node72 1.50, node73 8.37
node71, node89 104.50, node74 8.86, node91 284.64
node72, node76 15.32, node84 102.77, node92 133.06
node73, node83 52.22, node76 1.40, node90 243.00
node74, node81 1.07, node76 0.52, node78 8.08
node75, node92 68.53, node76 0.81, node77 1.19
node76, node85 13.18, node77 0.45, node78 2.36
node77, node80 8.94, node78 0.98, node86 64.32
node78, node98 355.90, node81 2.59
node79, node81 0.09, node85 1.45, node91 22.35
node80, node92 121.87, node88 28.78, node98 264.34
node81, node94 99.78, node89 39.52, node92 99.89
node82, node91 47.44, node88 28.05, node93 11.99
node83, node94 114.95, node86 8.75, node88 5.78
node84, node89 19.14, node94 30.41, node98 121.05
node85, node97 94.51, node87 2.66, node89 4.90
node86, node97 85.09
node87, node88 0.21, node91 11.14, node92 21.23
node88, node93 1.31, node91 6.83, node98 6.12
node89, node97 36.97, node99 82.12
node90, node96 23.53, node94 10.47, node99 50.99
node91, node97 22.17
node92, node96 10.83, node97 11.24, node99 34.68
node93, node94 0.19, node97 6.71, node99 32.77
node94, node98 5.91, node96 2.03
node95, node98 6.17, node99 0.27
node96, node98 3.32, node97 0.43, node99 5.87
node97, node98 0.30
node98, node99 0.33
node99,

Overwriting graph.txt

Solution to Exercise 37.1

首先，让我们编写一个函数，读取上面的图数据并构建一个距离矩阵。

num_nodes = 100
destination_node = 99

def map_graph_to_distance_matrix(in_file):

    # 首先，让我们用无穷大初始化距离矩阵Q
    Q = np.full((num_nodes, num_nodes), np.inf)

    # 现在我们读取数据并修改Q
    with open(in_file) as infile:
        for line in infile:
            elements = line.split(',')
            node = elements.pop(0)
            node = int(node[4:])    # 将节点描述转换为整数
            if node != destination_node:
                for element in elements:
                    destination, cost = element.split()
                    destination = int(destination[4:])
                    Q[node, destination] = float(cost)
            Q[destination_node, destination_node] = 0
    return Q

此外，让我们编写

一个”贝尔曼算子”函数，该函数接受距离矩阵和当前的J估计值，并返回更新后的J估计值，以及
一个函数，该函数接受距离矩阵并返回一个代价函数。我们将使用上述算法。最小化步骤被向量化以提高速度。

def bellman(J, Q):
    return np.min(Q + J, axis=1)


def compute_cost_to_go(Q):
    num_nodes = Q.shape[0]
    J = np.zeros(num_nodes)      # 初始猜测
    max_iter = 500
    i = 0

    while i < max_iter:
        next_J = bellman(J, Q)
        if np.allclose(next_J, J):
            break
        else:
            J[:] = next_J    # 将 next_J 的内容复制到 J
            i += 1

    return(J)

我们使用了 np.allclose() 而不是测试精确相等，因为我们现在处理的是浮点数。

最后，这里有一个函数，它使用代价函数来获取最优路径（及其成本）。

def print_best_path(J, Q):
    sum_costs = 0
    current_node = 0
    while current_node != destination_node:
        print(current_node)
       # 移动到下一个节点并增加成本
        next_node = np.argmin(Q[current_node, :] + J)
        sum_costs += Q[current_node, next_node]
        current_node = next_node

    print(destination_node)
    print('成本: ', sum_costs)

好了，现在我们已经有了必要的函数，让我们调用它们来完成我们被分配的任务。

Q = map_graph_to_distance_matrix('graph.txt')
J = compute_cost_to_go(Q)
print_best_path(J, Q)

0
8
11
18
23
33
41
53
56
57
60
67
70
73
76
85
87
88
93
94
96
97
98
99
成本:  160.55000000000007

路径的总成本应该与 \(J[0]\) 一致，所以让我们来验证一下。

J[0]

160.55