24. 索洛-斯旺增长模型#

在本讲中，我们将回顾一个由罗伯特·索洛（1925–2023）和特雷弗·斯旺（1918–1989）提出的著名模型。

这个模型被用于研究长期的经济增长。

尽管这是一个相对简单的模型，但它提供了许多关于经济增长的深刻见解。

我们将使用以下导入语句。

import matplotlib.pyplot as plt
import numpy as np

24.1. 模型#

在索洛-斯旺经济模型中，经济主体将其当前收入的固定比例用于储蓄。

这些储蓄维持或增加了资本存量。

资本与劳动力相结合生产产出，产出又支付给工人和资本所有者。

为了简化问题，我们忽略人口和生产力增长。

对于每个整数 $t \geq 0$ ，第 $t$ 期的产出 $Y_{t}$ 由 $Y_{t} = F (K_{t}, L_{t})$ 给出，其中 $K_{t}$ 是资本， $L_{t}$ 是劳动力， $F$ 是总生产函数。

假设函数 $F$ 是非负的，且是一阶齐次的，这意味着

F (λ K, λ L) = λ F (K, L) 对于所有 λ \geq 0

具有这种特性的生产函数包括：

Cobb-Douglas函数 $F (K, L) = A K^{α} L^{1 - α}$ ，其中 $0 \leq α \leq 1$ 。
CES函数 $F (K, L) = {a K^{ρ} + b L^{ρ}}^{1 / ρ}$ ，其中 $a, b, ρ > 0$ 。

这里， $α$ 是资本的产出弹性， $ρ$ 是决定资本和劳动力之间替代弹性的参数。

我们假设一个封闭经济，因此总国内投资等于总国内储蓄。

储蓄率是一个常数 $s$ ，满足 $0 \leq s \leq 1$ ，所以总投资和储蓄都等于 $s Y_{t}$ 。

资本会贬值：如果不通过投资补充，今天的一单位资本明天会变成 $1 - δ$ 单位。

因此，

K_{t + 1} = s F (K_{t}, L_{t}) + (1 - δ) K_{t}

没有人口增长， $L_{t}$ 等于某个常数 $L$ 。

令 $k_{t} := K_{t} / L$ ，并使用一阶齐次性，现在得到

k_{t + 1} = s \frac{F (K_{t}, L)}{L} + (1 - δ) \frac{K_{t}}{L} = s \frac{F (K_{t}, L)}{L} + (1 - δ) k_{t} = s F (k_{t}, 1) + (1 - δ) k_{t}

令 $f (k) := F (k, 1)$ ，资本动态的最终表达式为

(24.1)#

k_{t + 1} = g (k_{t}) where g (k) := s f (k) + (1 - δ) k

我们的目标是在给定外生初始资本存量 $k_{0}$ 的条件下，研究 $k_{t}$ 随时间演变的规律。

24.2. 图形化视角#

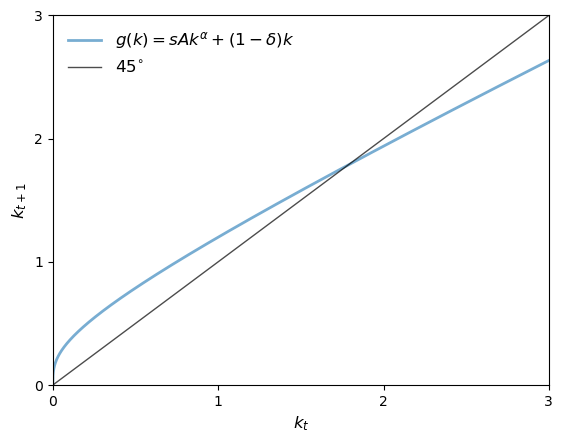
为了理解序列 $(k_{t})_{t \geq 0}$ 的动态，我们使用45度图。

为此，我们首先需要为 $f$ 指定函数形式并为参数赋值。

我们采用Cobb–Douglas生产函数 $f (k) = A k^{α}$ ，并设置参数值为 $A = 2.0$ ， $α = 0.3$ ， $s = 0.3$ 和 $δ = 0.4$ 。

然后绘制方程 (24.1) 中的函数 $g$ ，以及45度线。

我们定义这些常数如下

A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = 0.25
xmin, xmax = 0, 3

现在我们来定义函数 $g$

def g(A, s, alpha, delta, k):
    return A * s * k**alpha + (1 - delta) * k

让我们来绘制函数 $g$ 的45度图

def plot45(kstar=None):
    xgrid = np.linspace(xmin, xmax, 12000)

    fig, ax = plt.subplots()

    ax.set_xlim(xmin, xmax)

    g_values = g(A, s, alpha, delta, xgrid)

    ymin, ymax = np.min(g_values), np.max(g_values)
    ax.set_ylim(ymin, ymax)

    lb = r'$g(k) = sAk^{\alpha} + (1 - \delta)k$'
    ax.plot(xgrid, g_values,  lw=2, alpha=0.6, label=lb)
    ax.plot(xgrid, xgrid, 'k-', lw=1, alpha=0.7, label=r'$45^{\circ}$')

    if kstar:
        fps = (kstar,)

        ax.plot(fps, fps, 'go', ms=10, alpha=0.6)

        ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
                 xy=(kstar, kstar),
                 xycoords='data',
                 xytext=(-40, -60),
                 textcoords='offset points',
                 fontsize=14,
                 arrowprops=dict(arrowstyle="->"))

    ax.legend(loc='upper left', frameon=False, fontsize=12)

    ax.set_xticks((0, 1, 2, 3))
    ax.set_yticks((0, 1, 2, 3))

    ax.set_xlabel('$k_t$', fontsize=12)
    ax.set_ylabel('$k_{t+1}$', fontsize=12)

    plt.show()

plot45()

_images/eb2a0ba00ca8d7a87326646dfcc72fd65d591f85b30fd9993efc3e91ac1e034b.png

假设在某个 $k_{t}$ 处， $g (k_{t})$ 的值严格高于45度线。

那么我们有 $k_{t + 1} = g (k_{t}) > k_{t}$ ，则人均资本增加。

如果 $g (k_{t}) < k_{t}$ ，则人均资本下降。

如果 $g (k_{t}) = k_{t}$ ，那么我们就处于稳态， $k_{t}$ 保持不变。

（模型的稳态是映射 $g$ 的不动点。）

从图中可以看出， $g$ 函数与45度线只有一个交点，这意味着在 $(0, \infty)$ 区间内存在唯一的稳态。

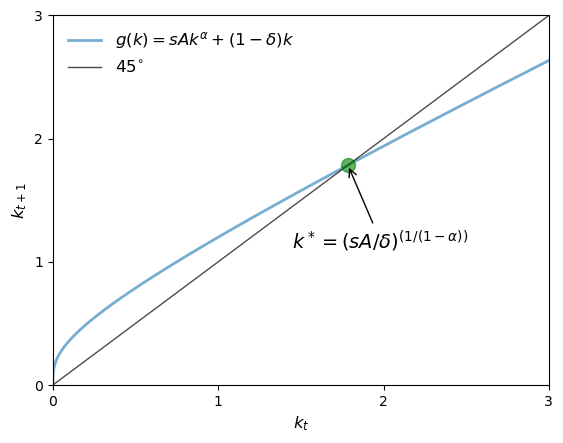
在稳态时， $k^{*} = g (k^{*})$ ，即 $k^{*} = s A (k^{*})^{α} + (1 - δ) k^{*}$ 。解这个方程，我们得到

(24.2)#

k^{*} := {(\frac{s A}{δ})}^{1 / (1 - α)}

当初始资本低于稳态值 $k^{*}$ 时，我们可以从图中看到 $g (k_{t}) > k_{t}$ ，这意味着资本存量会随时间增加，逐渐接近稳态。

相反，如果初始资本高于 $k^{*}$ ，则 $g (k_{t}) < k_{t}$ ，资本存量会随时间减少，同样趋向于稳态值。

让我们在45度图中标出这个稳态值 $k^{*}$ ，以便更直观地理解这一动态过程。

kstar = ((s * A) / delta)**(1/(1 - alpha))
plot45(kstar)

_images/fc30c38bacfd4aa9f3343cbf24614d332f18cc531cca19de891e9ba0d220de54.png

根据图示分析，无论初始资本存量 $k_{0}$ 如何， $k_{t}$ 都将收敛于稳态值 $k^{*}$ 。

这是一种全局稳定性的形式。

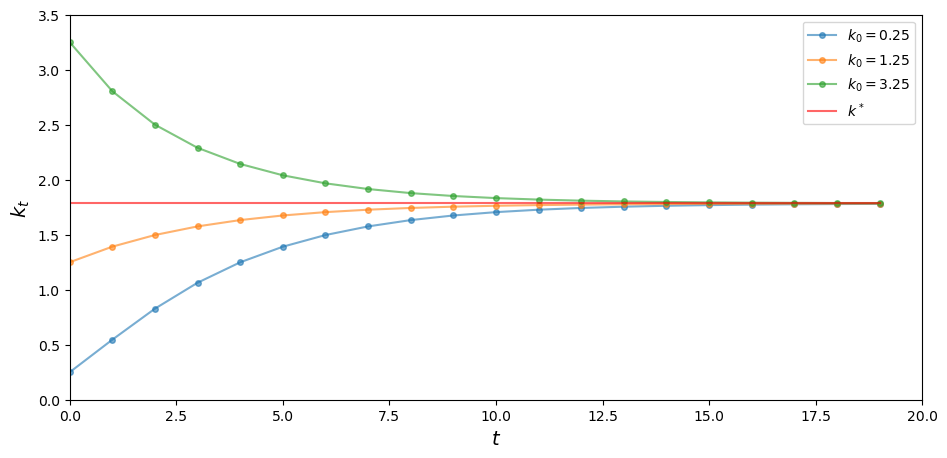
下图显示了在上述参数设置条件下，从三个不同的初始条件出发的资本时间路径。

在这种参数设置下， $k^{*} \approx 1.78$ 。

让我们定义常数和三个不同的初始条件

A, s, alpha, delta = 2, 0.3, 0.3, 0.4
x0 = np.array([.25, 1.25, 3.25])

ts_length = 20
xmin, xmax = 0, ts_length
ymin, ymax = 0, 3.5

def simulate_ts(x0_values, ts_length):

    k_star = (s * A / delta)**(1/(1-alpha))
    fig, ax = plt.subplots(figsize=[11, 5])
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(ymin, ymax)

    ts = np.zeros(ts_length)

    # 模拟和绘制时间序列
    for x_init in x0_values:
        ts[0] = x_init
        for t in range(1, ts_length):
            ts[t] = g(A, s, alpha, delta, ts[t-1])
        ax.plot(np.arange(ts_length), ts, '-o', ms=4, alpha=0.6,
                label=r'$k_0=%g$' %x_init)
    ax.plot(np.arange(ts_length), np.full(ts_length,k_star),
            alpha=0.6, color='red', label=r'$k^*$')
    ax.legend(fontsize=10)

    ax.set_xlabel(r'$t$', fontsize=14)
    ax.set_ylabel(r'$k_t$', fontsize=14)

    plt.show()

simulate_ts(x0, ts_length)

_images/cbc9f4786772249302319ae8e7a37935cad9515e3ec072122ccfb57cb38dadfe.png

如图所示，所有时间路径均如预期收敛至稳态值 $k^{*}$ 。

24.3. 连续时间的增长#

在本节中，我们将研究索洛-斯旺增长模型的连续时间版本。

连续时间框架提供了一种更为流畅的分析方法，使得模型的动态特性更容易理解。

让我们回顾一下离散时间版本的资本动态方程： $k_{t + 1} = s f (k_{t}) + (1 - δ) k_{t}$ 。

我们可以将其重新整理为单位时间内的变化量：

Δ k_{t} = s f (k_{t}) - δ k_{t} 其中 Δ k_{t} := k_{t + 1} - k_{t}

当我们让时间间隔无限趋近于零时，这个离散变化自然过渡到连续时间的导数形式

(24.3)#

k_{t}^{'} = s f (k_{t}) - δ k_{t} with k_{t}^{'} := \frac{d}{d t} k_{t}

我们的目标是在给定初始资本存量 $k_{0}$ 的条件下，研究 $k_{t}$ 随时间演变的规律。

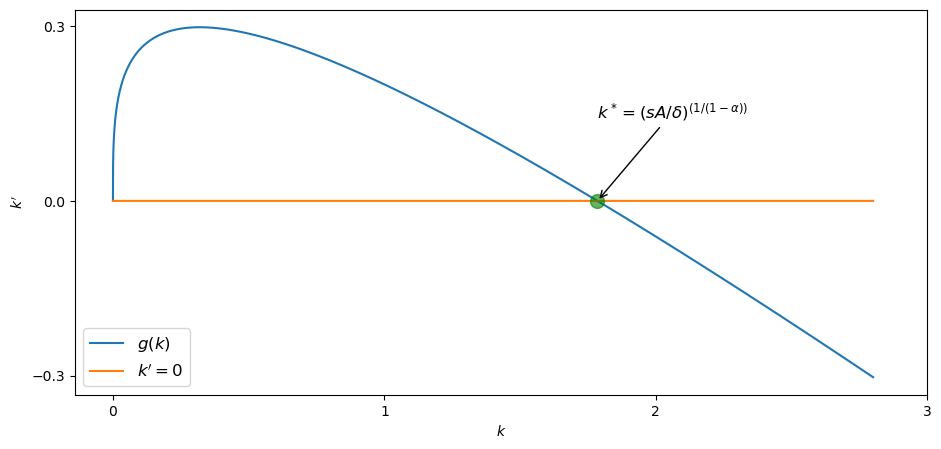
方程 (24.3) 的稳态是指资本存量保持不变的 $k^{*}$ ，即 $k_{t}^{'} = 0$ 或等价地， $s f (k^{*}) = δ k^{*}$ 。

我们假设 $f (k) = A k^{α}$ ，因此 $k^{*}$ 满足 $s A k^{α} = δ k$ 。

解法与离散时间情况相同——参见 (24.2)。

动态过程将在下一图表中呈现，并沿用上文所述的参数设定。

将 $k_{t}^{'} = g (k_{t})$ 定义为 $g (k) = s A k^{α} - δ k$ ，当 $g (k) > 0$ 时， $k_{t}^{'} > 0$ ，此时资本存量处于增长状态。

当 $g (k) < 0$ 时，资本存量将减少。这种动态机制源于两种力量的共同作用：低资本存量水平下的储蓄高边际回报与高资本存量水平下的低回报率相结合，最终形成系统的全局稳定性。

为了在图中看到这一点，让我们定义以下常数

A, s, alpha, delta = 2, 0.3, 0.3, 0.4

接下来，我们定义函数 $g$ 表示连续时间的增长

def g_con(A, s, alpha, delta, k):
    return A * s * k**alpha - delta * k

def plot_gcon(kstar=None):

    k_grid = np.linspace(0, 2.8, 10000)

    fig, ax = plt.subplots(figsize=[11, 5])
    ax.plot(k_grid, g_con(A, s, alpha, delta, k_grid), label='$g(k)$')
    ax.plot(k_grid, 0 * k_grid, label="$k'=0$")

    if kstar:
        fps = (kstar,)

        ax.plot(fps, 0, 'go', ms=10, alpha=0.6)


        ax.annotate(r'$k^* = (sA / \delta)^{(1/(1-\alpha))}$',
                 xy=(kstar, 0),
                 xycoords='data',
                 xytext=(0, 60),
                 textcoords='offset points',
                 fontsize=12,
                 arrowprops=dict(arrowstyle="->"))

    ax.legend(loc='lower left', fontsize=12)

    ax.set_xlabel("$k$",fontsize=10)
    ax.set_ylabel("$k'$", fontsize=10)

    ax.set_xticks((0, 1, 2, 3))
    ax.set_yticks((-0.3, 0, 0.3))

    plt.show()

kstar = ((s * A) / delta)**(1/(1 - alpha))
plot_gcon(kstar)

_images/53d167007c17b9383b6f28b82560e13a18f37b38c767901492506b6912171ba3.png

上图直观地展示了特定参数下的全局稳定性，但我们如何严格证明这一性质对于所有合理参数都成立呢？

在离散时间模型中，要得到 $k_{t}$ 的解析表达式相当困难。

然而，转向连续时间框架可以大大简化分析。在连续时间下，我们能够推导出 $k_{t}$ 的简洁表达式，从而清晰地描述资本存量随时间的演化路径。

为此，我们引入变量替换 $x_{t} := k_{t}^{1 - α}$ ，这样 $x_{t}^{'} = (1 - α) k_{t}^{- α} k_{t}^{'}$ 。

将连续时间的动态方程 $k_{t}^{'} = s A k_{t}^{α} - δ k_{t}$ 代入上式，我们得到一个线性微分方程

(24.4)#

x_{t}^{'} = (1 - α) (s A - δ x_{t})

这个方程是一个线性常微分方程，其解为 $ $x_{t} = (k_{0}^{1 - α} - \frac{s A}{δ}) e^{- δ (1 - α) t} + \frac{s A}{δ}$ $

（你可以通过对 $t$ 求导来确认这个函数 $x_{t}$ 满足方程(24.4)。）

代换回 $k_{t}$ 得到

(24.5)#

k_{t} = {[(k_{0}^{1 - α} - \frac{s A}{δ}) e^{- δ (1 - α) t} + \frac{s A}{δ}]}^{1 / (1 - α)}

由于 $δ > 0$ 且 $α \in (0, 1)$ ，我们立即可以得出结论，当 $t \to \infty$ 时， $k_{t} \to k^{*}$ ，且与 $k_{0}$ 无关。

因此，全局稳定性成立。

24.4. 练习#

Exercise 24.1

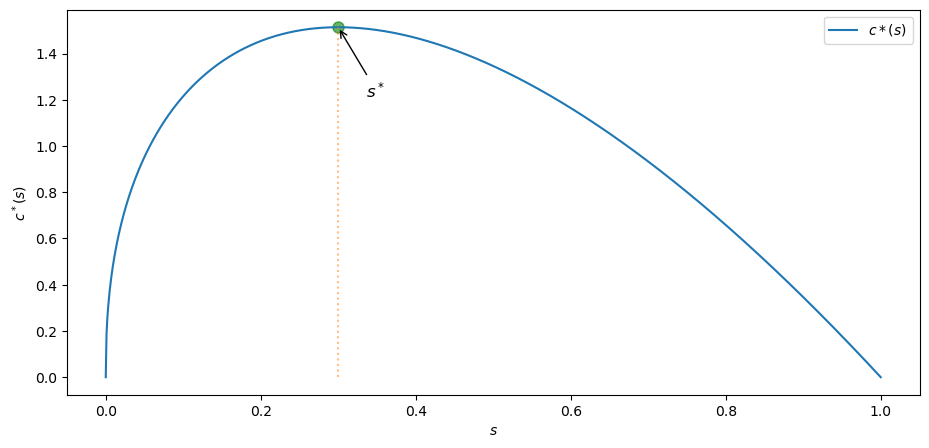
绘制稳态下人均消费 $c$ 作为储蓄率 $s$ 的函数图，其中 $0 \leq s \leq 1$ 。

使用Cobb-Douglas生产函数 $f (k) = A k^{α}$ 。

设 $A = 2.0, α = 0.3,$ 且 $δ = 0.5$ 。

此外，找出能使 $c^{*} (s)$ 最大化的 $s$ 的近似值，并在图中表示。

Solution to Exercise 24.1

在储蓄率 $s$ 下的稳态消费由以下公式给出：

c^{*} (s) = (1 - s) f (k^{*}) = (1 - s) A (k^{*})^{α}

A = 2.0
alpha = 0.3
delta = 0.5

s_grid = np.linspace(0, 1, 1000)
k_star = ((s_grid * A) / delta)**(1/(1 - alpha))
c_star = (1 - s_grid) * A * k_star ** alpha

让我们使用 scipy.optimize.minimize_scalar 来找出使 $c^{*}$ 最大化的 $s$ 值。

我们将使用 $- c^{*} (s)$ ，因为 minimize_scalar 函数是用来寻找最小值的。

from scipy.optimize import minimize_scalar

def calc_c_star(s):
    k = ((s * A) / delta)**(1/(1 - alpha))
    return - (1 - s) * A * k ** alpha

return_values = minimize_scalar(calc_c_star, bounds=(0, 1))
s_star_max = return_values.x
c_star_max = -return_values.fun
print(f"Function is maximized at s = {round(s_star_max, 4)}")

Function is maximized at s = 0.3

x_s_max = np.array([s_star_max, s_star_max])
y_s_max = np.array([0, c_star_max])

fig, ax = plt.subplots(figsize=[11, 5])

fps = (c_star_max,)

# 用标记突出显示最大点
ax.plot((s_star_max, ), (c_star_max,), 'go', ms=8, alpha=0.6)

ax.annotate(r'$s^*$',
         xy=(s_star_max, c_star_max),
         xycoords='data',
         xytext=(20, -50),
         textcoords='offset points',
         fontsize=12,
         arrowprops=dict(arrowstyle="->"))
ax.plot(s_grid, c_star, label=r'$c*(s)$')
ax.plot(x_s_max, y_s_max, alpha=0.5, ls='dotted')
ax.set_xlabel(r'$s$')
ax.set_ylabel(r'$c^*(s)$')
ax.legend()

plt.show()

_images/9cb908e3ee7d14ec4cb105fa711466b47baa63cfbb08359009077feaf2bc65cb.png

我们也可以尝试用数学方法解决这个问题，即对 $c^{*} (s)$ 进行微分，并使用 sympy 求解 $\frac{d}{d s} c^{*} (s) = 0$ 。

from sympy import solve, Symbol

s_symbol = Symbol('s', real=True)
k = ((s_symbol * A) / delta)**(1/(1 - alpha))
c = (1 - s_symbol) * A * k ** alpha

让我们对 $c$ 进行微分，并使用 sympy.solve 求解。

# 使用 sympy 求解
s_star = solve(c.diff())[0]
print(f"s_star = {s_star}")

s_star = 0.300000000000000

顺便说一下，使人均消费的稳态水平最大化的储蓄率被称为经济增长黄金律。

Exercise 24.2

随机生产率

为了使索洛-斯旺模型更贴近实际数据，我们需要考虑如何处理总量中的随机波动。

这样做会带来多方面的影响，其中之一是消除了人均产出 $y_{t} = A k_{t}^{α}$ 收敛到常数 $y^{*} := A (k^{*})^{α}$ 这一不切实际的预测。

接下来，我们将转向对离散时间模型的讨论。

一种方法是用某个随机序列 $(A_{t})_{t \geq 1}$ 替代常数生产率。

现在的动态方程变为

(24.6)#

k_{t + 1} = s A_{t + 1} f (k_{t}) + (1 - δ) k_{t}

我们假设 $f$ 是Cobb–Douglas生产函数，且 $(A_{t})$ 是独立同分布的对数正态分布。

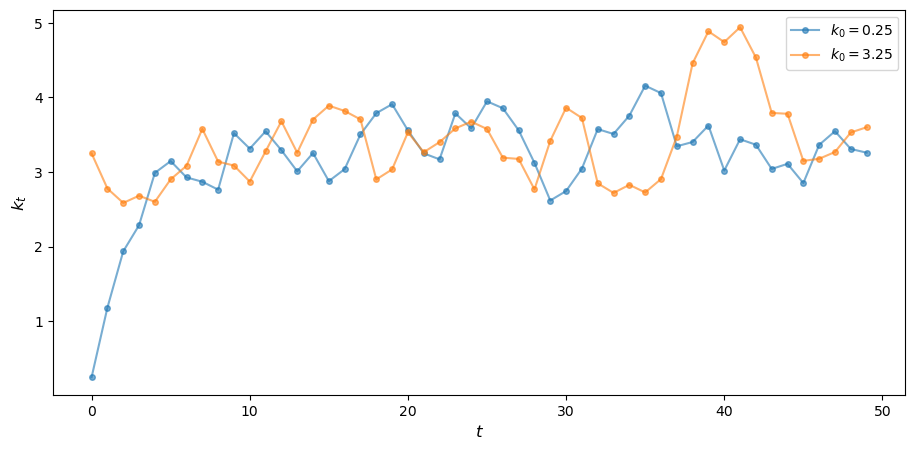
现在，在确定性情况下获得的长期收敛性不再成立，因为系统在每个时间点都会受到新的冲击。

考虑 $A = 2.0, s = 0.6, α = 0.3,$ 且 $δ = 0.5$ 。

生成并绘制时间序列 $k_{t}$ 的图表。

Solution to Exercise 24.2

让我们定义用于模拟的对数正态分布的常数和初始值

# 定义常数
sig = 0.2
mu = np.log(2) - sig**2 / 2
A = 2.0
s = 0.6
alpha = 0.3
delta = 0.5
x0 = [.25, 3.25] # 用于模拟的初始值列表

让我们定义函数 k_next 来找出 $k$ 的下一个值

def lgnorm():
    return np.exp(mu + sig * np.random.randn())

def k_next(s, alpha, delta, k):
    return lgnorm() * s * k**alpha + (1 - delta) * k

def ts_plot(x_values, ts_length):
    fig, ax = plt.subplots(figsize=[11, 5])
    ts = np.zeros(ts_length)

    # 模拟并且绘制时间序列
    for x_init in x_values:
        ts[0] = x_init
        for t in range(1, ts_length):
            ts[t] = k_next(s, alpha, delta, ts[t-1])
        ax.plot(np.arange(ts_length), ts, '-o', ms=4,
                alpha=0.6, label=r'$k_0=%g$' %x_init)

    ax.legend(loc='best', fontsize=10)

    ax.set_xlabel(r'$t$', fontsize=12)
    ax.set_ylabel(r'$k_t$', fontsize=12)


    plt.show()

ts_plot(x0, 50)

_images/2cb782217f1fc69b5b96fea012e7d81dcc141562c34f919362463628e1bca7b8.png