13. 均衡差异模型#

13.1. 概述#

本讲座介绍了一个研究大学与高中毕业生工资差距的模型，其中获得大学学历所需的时间是关键因素。

这个模型最初由米尔顿·弗里德曼创建，用于研究美国牙医和医生的收入差异——他想弄清这种差异是竞争性劳动力市场的自然结果，还是源于政府与医疗专业组织设置的准入门槛。

詹妮弗·伯恩斯在其著作[Burns, 2023]第4章中，详细描述了米尔顿·弗里德曼与西蒙·库兹涅茨的合作研究，这项研究最终促成了[Kuznets and Friedman, 1939]和[Friedman and Kuznets, 1945]的发表。

我们可以将弗里德曼的模型对应到我们的研究中：把高中毕业生对应于牙医，把大学毕业生对应于医生。

我们提供的是一个简化模型，仅包含一个方程。在更完整的模型中，这个方程将是多个均衡条件之一。

这个”均衡差异”方程确定了使高中和大学毕业生终身收入现值相等的工资比率。

其基本思想是：工资水平会自动调整，直到高中应届毕业生在”直接工作”和”继续上大学”这两个选择之间无差别。

（在更完整的模型中，其他方程会解释是什么因素推动了这种调整。）

我们的模型是相对工资”均衡差异”理论的一个具体应用。这类理论可以追溯到亚当·斯密的《国富论》[Smith, 2010]。

本讲座主要使用线性代数知识，特别是矩阵乘法和矩阵求逆。

在讲座末尾，我们会引入一些微积分内容，展示如何用偏导数更简洁地表达某些结论。

这也让我们有机会展示Python在处理微积分计算时的强大功能！

不过即使不懂微积分，掌握线性代数知识也足以理解核心内容。

首先，让我们导入所需的Python模块。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

13.2. 无差异条件#

这个模型的关键在于：大学教育带来的额外工资收益会达到一个均衡点，在这个点上，普通工人选择上大学或直接工作的预期收益是相等的。

设：

$R > 1$ 为一期债券的总回报率
$t = 0, 1, 2, \dots T$ 表示一个人工作或上大学的年数
$0$ 表示一个人如果不上大学高中毕业后可以工作的第一个时期
$T$ 表示一个人工作的最后一个时期
$w_{t}^{h}$ 为高中毕业生在 $t$ 时的工资
$w_{t}^{c}$ 为大学毕业生在 $t$ 时的工资
$γ_{h} > 1$ 为高中毕业生工资的（总）增长率，使得 $w_{t}^{h} = w_{0}^{h} γ_{h}^{t}$
$γ_{c} > 1$ 为大学毕业生工资的（总）增长率，使得 $w_{t}^{c} = w_{0}^{c} γ_{c}^{t}$
$D$ 为上大学所需的成本

现在我们考虑一个新的高中毕业生所面临的两个选择：

立即工作并赚取高中毕业生的工资
上大学四年，毕业后赚取大学毕业生的工资

并计算这位毕业生所能获得的现值

13.2.1. 不上大学直接工作的现值#

如果某人高中毕业后立即工作，并在 $t = 0, 1, 2, \dots, T$ 的 $T + 1$ 年内工作，她赚取的现值为：

h_{0} = \sum_{t = 0}^{T} R^{- t} w_{t}^{h} = w_{0}^{h} [\frac{1 - (R^{- 1} γ_{h})^{T + 1}}{1 - R^{- 1} γ_{h}}] \equiv w_{0}^{h} A_{h}

其中

A_{h} = [\frac{1 - (R^{- 1} γ_{h})^{T + 1}}{1 - R^{- 1} γ_{h}}] .

现值 $h_{0}$ 是选择不上大学而是立即以高中毕业生的工资开始工作的人在时间 $0$ 开始时的”人力财富”。

13.2.2. 上大学后工作的现值#

如果某人在 $t = 0, 1, 2, 3$ 的四年内上大学，期间收入为 $0$ ，但在大学毕业后立即工作，并在 $t = 4, 5, \dots, T$ 的 $T - 3$ 年内工作，她赚取的现值为：

c_{0} = \sum_{t = 4}^{T} R^{- t} w_{t}^{c} = w_{0}^{c} (R^{- 1} γ_{c})^{4} [\frac{1 - (R^{- 1} γ_{c})^{T - 3}}{1 - R^{- 1} γ_{c}}] \equiv w_{0}^{c} A_{c}

其中

A_{c} = (R^{- 1} γ_{c})^{4} [\frac{1 - (R^{- 1} γ_{c})^{T - 3}}{1 - R^{- 1} γ_{c}}] .

现值 $c_{0}$ 是选择上大学四年然后在 $t = 4$ 时以大学毕业生的工资开始工作的人在时间 $0$ 开始时的”人力财富”。

假设大学学费加上四年的食宿费用总计为 $D$ ，必须在时间 $0$ 付清。

因此，扣除上大学的货币成本后，高中毕业后第一个时期上大学的现值为：

c_{0} - D

现在我们制定一个纯均衡差异模型，用于设定大学-高中工资的初始差距 $ϕ$ ，其中：

w_{0}^{c} = ϕ w_{0}^{h}

我们假设 $R, γ_{h}, γ_{c}, T$ 以及 $w_{0}^{h}$ 是固定参数。

首先，均衡差异模型揭示了一个重要关系：大学与高中毕业生的工资差距 $ϕ$ 需要满足一个”均衡”方程。在这个方程中，选择不上大学直接工作的终身收入现值，应该等于选择上大学后工作的终身收入现值：

h_{0} = c_{0} - D

或

(13.1)#

w_{0}^{h} A_{h} = ϕ w_{0}^{h} A_{c} - D .

这个”无差异条件”是模型的核心。

求解方程 (13.1) 得到大学工资溢价 $ϕ$ ：

(13.2)#

ϕ = \frac{A_{h}}{A_{c}} + \frac{D}{w_{0}^{h} A_{c}} .

在免费大学的特殊情况下， $D = 0$ 。

在这种情况下，上大学的唯一成本是放弃作为高中学历工人的收入。

因此，

ϕ = \frac{A_{h}}{A_{c}} .

我们很快将编写 Python 代码来计算 $ϕ$ 并绘制它的函数图。

但首先，我们重新解读这些变量并描述我们模型的一种新的解释。

13.3. 重新解读模型：打工人和企业家#

我们可以通过添加一个参数并重新解读变量来获得一个有关企业家和打工人的模型。

现在让 $h$ 表示”打工人”的现值。

我们将企业家的现值定义为：

c_{0} = π \sum_{t = 4}^{T} R^{- t} w_{t}^{c}

其中 $π \in (0, 1)$ 是企业家的”项目”成功的概率。

对于我们的打工人和企业家模型，我们将把 $D$ 解释为成为企业家的成本。

这个成本可能包括雇佣工人、办公空间和律师的费用。

我们过去称之为大学、高中工资差距的 $ϕ$ 现在变成了成功企业家收入与打工人收入的比率。

我们会发现，随着 $π$ 的减少， $ϕ$ 会增加，这表明成为企业家的风险越大，成功项目的回报就必须越高。

13.4. 计算#

通过变动参数 $γ_{h}, γ_{c}, R$ ，我们可以创建出一些有趣的例子。

现在让我们编写一些 Python 代码来计算 $ϕ$ 并绘制其与某些决定因素的关系。

class equalizing_diff:
    """
    均等差异模型的一个类
    """
    
    def __init__(self, R, T, γ_h, γ_c, w_h0, D=0, π=None):
        # 通过设置 π 切换到弱模型
        self.R, self.γ_h, self.γ_c, self.w_h0, self.D = R, γ_h, γ_c, w_h0, D
        self.T, self.π = T, π
    
    def compute_gap(self):
        R, γ_h, γ_c, w_h0, D = self.R, self.γ_h, self.γ_c, self.w_h0, self.D
        T, π = self.T, self.π
        
        A_h = (1 - (γ_h/R)**(T+1)) / (1 - γ_h/R)
        A_c = (1 - (γ_c/R)**(T-3)) / (1 - γ_c/R) * (γ_c/R)**4
        
        # 调整后的模型
        if π!=None:
            A_c = π*A_c 
        
        ϕ = A_h/A_c + D/(w_h0*A_c)
        return ϕ

为了帮助我们进行比较静态分析，我们使用向量化而不是循环来构建一些函数。

对于类的给定实例，我们想在一个参数变化而其他参数保持固定时重新计算 $ϕ$ 。

举个例子：

# ϕ_R
def ϕ_R(mc, R_new):
    mc_new = equalizing_diff(R_new, mc.T, mc.γ_h, mc.γ_c, mc.w_h0, mc.D, mc.π)
    return mc_new.compute_gap()

ϕ_R = np.vectorize(ϕ_R)

# ϕ_γh
def ϕ_γh(mc, γh_new):
    mc_new = equalizing_diff(mc.R, mc.T, γh_new, mc.γ_c, mc.w_h0, mc.D, mc.π)
    return mc_new.compute_gap()

ϕ_γh = np.vectorize(ϕ_γh)

# ϕ_γc
def ϕ_γc(mc, γc_new):
    mc_new = equalizing_diff(mc.R, mc.T, mc.γ_h, γc_new, mc.w_h0, mc.D, mc.π)
    return mc_new.compute_gap()

ϕ_γc = np.vectorize(ϕ_γc)

# ϕ_π
def ϕ_π(mc, π_new):
    mc_new = equalizing_diff(mc.R, mc.T, mc.γ_h, mc.γ_c, mc.w_h0, mc.D, π_new)
    return mc_new.compute_gap()

ϕ_π = np.vectorize(ϕ_π)

# 设定标准参数
R = 1.05
T = 40
γ_h, γ_c = 1.01, 1.01
w_h0 = 1
D = 10

# 创建一个例子
ex1 = equalizing_diff(R=R, T=T, γ_h=γ_h, γ_c=γ_c, w_h0=w_h0, D=D)
gap1 = ex1.compute_gap()

print(gap1)

1.8041412724969135

假设大学不收费，然后重新计算 $ϕ$ 。

初始的大学工资溢价应该会降低。

# 免费大学
ex2 = equalizing_diff(R, T, γ_h, γ_c, w_h0, D=0)
gap2 = ex2.compute_gap()
print(gap2)

1.2204649517903732

让我们构建一些图表，展示如果初始大学-高中工资比率 $ϕ$ 的某个决定因素发生变化， $ϕ$ 将如何改变。

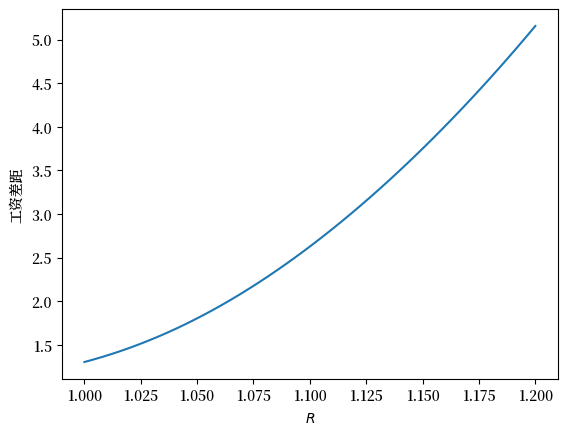
我们先从总利率 $R$ 开始。

R_arr = np.linspace(1, 1.2, 50)
plt.plot(R_arr, φ_R(ex1, R_arr))
plt.xlabel(r'$R$')
plt.ylabel(r'工资差距')
plt.show()

_images/a7ddf47b3931b8616096007970398f8cf67fc6716861b19bd96797f57e2b56fc.png

注意当大学工资增长率 $γ_{c}$ 上升时，初始工资差距是如何下降的。

工资差距下降是为了”平衡”两种职业类型的现值，一种是高中工人，另一种是大学工人。

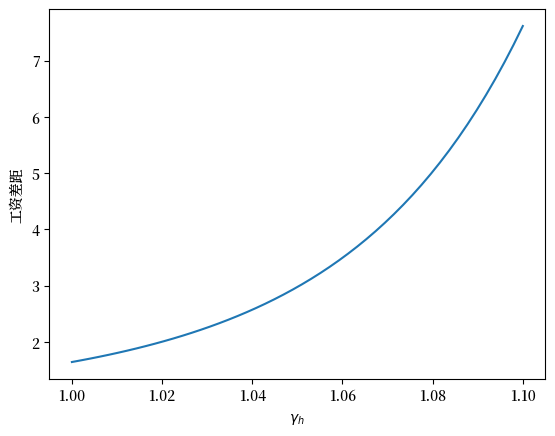
给定其它参数不变，你能猜到我们改变高中学历工人的工资的增长率时，初始工资比率 $ϕ$ 会发生什么变化吗？

下图显示了会发生什么。

γh_arr = np.linspace(1, 1.1, 50)
plt.plot(γh_arr, φ_γh(ex1, γh_arr))
plt.xlabel(r'$\gamma_h$')
plt.ylabel(r'工资差距')
plt.show()

_images/7188d4af0882dd4a941129f6d157c796b55231f73a106ba84c2f9006dbed88f8.png

13.5. 企业家和打工人#

现在让我们用企业家-打工人的视角来解读这个模型。

如果一个新企业成功的概率是 $0.2$ ，让我们计算成功企业家的初始工资溢价。

# 企业家模型
ex3 = equalizing_diff(R, T, γ_h, γ_c, w_h0, π=0.2)
gap3 = ex3.compute_gap()

print(gap3)

6.102324758951866

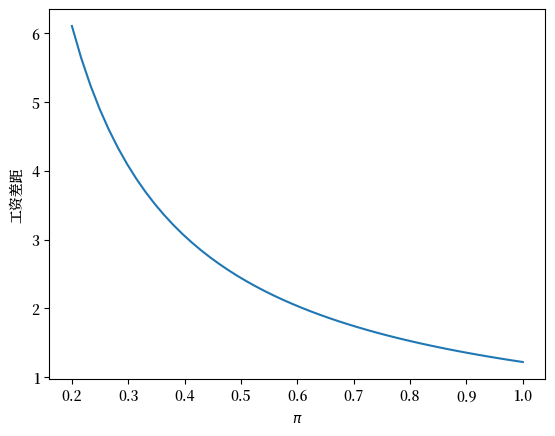
现在让我们研究成功企业家的初始工资溢价是如何依赖于成功概率的。

π_arr = np.linspace(0.2, 1, 50)
plt.plot(π_arr, φ_π(ex3, π_arr))
plt.ylabel(r'工资差距')
plt.xlabel(r'$\pi$')
plt.show()

_images/09df9f803b6b8c63ce74170b774d1fb1d347fcd2d000d9b0fbc2327793f90c76.png

这个图表是不是符合你的猜想呢？

13.6. 微积分的应用#

到目前为止，我们只使用了线性代数，这对我们理解模型的运作原理已经足够了。

然而，懂得微积分的人可能会希望我们直接求偏导数。

还不会微积分的读者可以不用继续往下读，因为线性代数已经让我们了解了模型的主要特性。

但对于那些有兴趣了解我们如何让 Python 计算偏导数的读者，我们接下来会讲解这些内容。

我们将使用 Python 模块 sympy 来计算 $ϕ$ 对决定它的参数的偏导数。

让我们从 sympy 导入关键函数。

from sympy import Symbol, Lambda, symbols

设定符号

γ_h, γ_c, w_h0, D = symbols(r'\gamma_h, \gamma_h_c, w_0^h, D', real=True)
R, T = Symbol('R', real=True), Symbol('T', integer=True)

设定函数 $A_{h}$

A_h = Lambda((γ_h, R, T), (1 - (γ_h/R)**(T+1)) / (1 - γ_h/R))
A_h

((γ_{h}, R, T) \mapsto \frac{1 - {(\frac{γ_{h}}{R})}^{T + 1}}{1 - \frac{γ_{h}}{R}})

设定函数 $A_{c}$

A_c = Lambda((γ_c, R, T), (1 - (γ_c/R)**(T-3)) / (1 - γ_c/R) * (γ_c/R)**4)
A_c

((γ_{h c}, R, T) \mapsto \frac{γ_{h c}^{4} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})}{R^{4} (1 - \frac{γ_{h c}}{R})})

设定 $ϕ$

ϕ = Lambda((D, γ_h, γ_c, R, T, w_h0), A_h(γ_h, R, T)/A_c(γ_c, R, T) + D/(w_h0*A_c(γ_c, R, T)))

ϕ

((D, γ_{h}, γ_{h c}, R, T, w_{0}^{h}) \mapsto \frac{D R^{4} (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{4} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})})

我们开始设定默认的参数值。

R_value = 1.05
T_value = 40
γ_h_value, γ_c_value = 1.01, 1.01
w_h0_value = 1
D_value = 10

现在让我们计算 $\frac{\partial ϕ}{\partial D}$ 然后计算其给定默认参数的值

ϕ_D = ϕ(D, γ_h, γ_c, R, T, w_h0).diff(D)
ϕ_D

\frac{R^{4} (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})}

# 给定默认参数的值
ϕ_D_func = Lambda((D, γ_h, γ_c, R, T, w_h0), ϕ_D)
ϕ_D_func(D_value, γ_h_value, γ_c_value, R_value, T_value, w_h0_value)

0.058367632070654

因此，与我们之前的图表一样，我们发现提高 $R$ 会增加初始大学工资溢价 $ϕ$ 。

计算 $\frac{\partial ϕ}{\partial T}$ 并代入默认参数值

ϕ_T = ϕ(D, γ_h, γ_c, R, T, w_h0).diff(T)
ϕ_T

\frac{D R^{4} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - \frac{γ_{h c}}{R}) \log (\frac{γ_{h c}}{R})}{γ_{h c}^{4} w_{0}^{h} {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}} - \frac{R^{4} {(\frac{γ_{h}}{R})}^{T + 1} (1 - \frac{γ_{h c}}{R}) \log (\frac{γ_{h}}{R})}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{4} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R}) \log (\frac{γ_{h c}}{R})}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}}

# 在默认值的值
ϕ_T_func = Lambda((D, γ_h, γ_c, R, T, w_h0), ϕ_T)
ϕ_T_func(D_value, γ_h_value, γ_c_value, R_value, T_value, w_h0_value)

- 0.00973478032996598

我们发现提高 $T$ 会降低初始大学工资溢价 $ϕ$ 。

这是因为大学毕业生现在有更长的职业生涯来”收回”他们为上大学付出的时间和其他成本。

让我们计算 $\frac{\partial ϕ}{\partial γ_{h}}$ 并代入默认参数值

ϕ_γ_h = ϕ(D, γ_h, γ_c, R, T, w_h0).diff(γ_h)
ϕ_γ_h

- \frac{R^{4} {(\frac{γ_{h}}{R})}^{T + 1} (1 - \frac{γ_{h c}}{R}) (T + 1)}{γ_{h} γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{3} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} {(1 - \frac{γ_{h}}{R})}^{2} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})}

# 在默认值的值
ϕ_γ_h_func = Lambda((D, γ_h, γ_c, R, T, w_h0), ϕ_γ_h)
ϕ_γ_h_func(D_value, γ_h_value, γ_c_value, R_value, T_value, w_h0_value)

17.8590485545256

我们发现提高 $γ_{h}$ 会增加初始大学工资溢价 $ϕ$ ，这与我们之前的图形分析结果一致。

计算 $\frac{\partial ϕ}{\partial γ_{c}}$ 并代入默认参数值

ϕ_γ_c = ϕ(D, γ_h, γ_c, R, T, w_h0).diff(γ_c)
ϕ_γ_c

\frac{D R^{4} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - \frac{γ_{h c}}{R}) (T - 3)}{γ_{h c}^{5} w_{0}^{h} {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}} - \frac{4 D R^{4} (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{5} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} - \frac{D R^{3}}{γ_{h c}^{4} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{4} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R}) (T - 3)}{γ_{h c}^{5} (1 - \frac{γ_{h}}{R}) {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}} - \frac{4 R^{4} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{5} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} - \frac{R^{3} (1 - {(\frac{γ_{h}}{R})}^{T + 1})}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})}

# 在默认值的值
ϕ_γ_c_func = Lambda((D, γ_h, γ_c, R, T, w_h0), ϕ_γ_c)
ϕ_γ_c_func(D_value, γ_h_value, γ_c_value, R_value, T_value, w_h0_value)

- 31.6486401973376

我们发现提高 $γ_{c}$ 会降低初始大学工资溢价 $ϕ$ ，这与我们之前的图形分析结果一致。

让我们计算 $\frac{\partial ϕ}{\partial R}$ 并代入默认参数值

ϕ_R = ϕ(D, γ_h, γ_c, R, T, w_h0).diff(R)
ϕ_R

- \frac{D R^{3} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - \frac{γ_{h c}}{R}) (T - 3)}{γ_{h c}^{4} w_{0}^{h} {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}} + \frac{4 D R^{3} (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{D R^{2}}{γ_{h c}^{3} w_{0}^{h} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{3} {(\frac{γ_{h}}{R})}^{T + 1} (1 - \frac{γ_{h c}}{R}) (T + 1)}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} - \frac{R^{3} {(\frac{γ_{h c}}{R})}^{T - 3} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R}) (T - 3)}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) {(1 - {(\frac{γ_{h c}}{R})}^{T - 3})}^{2}} + \frac{4 R^{3} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} - \frac{R^{2} γ_{h} (1 - {(\frac{γ_{h}}{R})}^{T + 1}) (1 - \frac{γ_{h c}}{R})}{γ_{h c}^{4} {(1 - \frac{γ_{h}}{R})}^{2} (1 - {(\frac{γ_{h c}}{R})}^{T - 3})} + \frac{R^{2} (1 - {(\frac{γ_{h}}{R})}^{T + 1})}{γ_{h c}^{3} (1 - \frac{γ_{h}}{R}) (1 - {(\frac{γ_{h c}}{R})}^{T - 3})}

# 在默认值的值
ϕ_R_func = Lambda((D, γ_h, γ_c, R, T, w_h0), ϕ_R)
ϕ_R_func(D_value, γ_h_value, γ_c_value, R_value, T_value, w_h0_value)

13.2642738659429

我们发现提高总利率 $R$ 会增加初始大学工资溢价 $ϕ$ ，这也与我们之前的图形分析结果一致。