11. 现值

11.1. 概述

本讲座描述了现值模型，这是许多资产定价理论的起点。

资产定价理论是许多经济决策理论的组成部分，包括

• 消费

• 劳动力供给

• 教育选择

• 货币需求

在资产定价理论以及更广泛的经济动态研究中，一个基本主题是不同时间序列之间的关系。

时间序列是按时间索引的序列。

在本讲座中，我们将把序列表示为向量。

因此，我们的分析通常归结为研究向量之间的关系。

本讲座中的主要工具将是

• 矩阵乘法，和

• 矩阵求逆。

我们将在后续的许多讲座中使用这些工具，包括消费平滑，均衡差异模型，和货币主义价格水平理论。

让我们开始吧。

11.2. 分析

设

• \(\{d_t\}_{t=0}^T \) 是一系列股息或“支付”

• \(\{p_t\}_{t=0}^T \) 是从时间\(t\)开始的延续性的资产支付价格序列，即\(\{d_s\}_{s=t}^T \)

• \( \delta \in (0,1) \) 是一个周期的“折现因子”

• \(p_{T+1}^*\) 是\(T+1\)时资产的终端价格

我们假设股息序列\(\{d_t\}_{t=0}^T \)和终端价格\(p_{T+1}^*\)都是外生的。

这意味着它们是在模型之外确定的。

假设资产定价方程序列

(11.1)\[ p_t = d_t + \delta p_{t+1}, \quad t = 0, 1, \ldots , T \]

我们称其为方程序列，因为有\(T+1\)个方程，每个\(t =0, 1, \ldots, T\)都有一个。

方程(11.1)告诉我们在时间\(t\)购买资产所支付的价格等于支付\(d_t\)加上时间\(t+1\)的价格乘以时间折现因子\(\delta\)。

通过将明天的价格乘以\(\delta\)来折现，考虑了“等待一个周期的价值”。

我们想要解\(T+1\)个方程(11.1)的系统，以资产价格序列\(\{p_t\}_{t=0}^T \)作为股息序列\(\{d_t\}_{t=0}^T \)和外生终端价格\(p_{T+1}^*\)的函数。

像(11.1)这样的方程系统是线性差分方程的一个例子。

有许多强大的数学方法可以用来解决这样的系统，这些方法本身就很值得研究，因为它们是分析许多经济模型的基础。

例如，参见Samuelson乘数-加速器

在本讲座中，我们将使用矩阵乘法和矩阵求逆来解决系统(11.1)，这是线性代数中的基本工具，在线性方程和矩阵代数中有介绍。

我们将导入以下的库

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import font_manager
fontP = font_manager.FontProperties()
fontP.set_family('SimHei')
fontP.set_size(14)

11.3. 将序列表示为向量

系统(11.1)中的方程可以如下排列：

(11.2)\[\begin{split} \begin{aligned} p_0 & = d_0 + \delta p_1 \\ p_1 & = d_1 + \delta p_2 \\ \vdots \\ p_{T-1} & = d_{T-1} + \delta p_T \\ p_T & = d_T + \delta p^*_{T+1} \end{aligned} \end{split}\]

将\(T+1\)个资产定价方程的系统(11.2)写成单个矩阵方程

(11.3)\[ \begin{bmatrix} 1 & -\delta & 0 & 0 & \cdots & 0 & 0 \cr 0 & 1 & -\delta & 0 & \cdots & 0 & 0 \cr 0 & 0 & 1 & -\delta & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & 0 & 0 \cr 0 & 0 & 0 & 0 & \cdots & 1 & -\delta \cr 0 & 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \begin{bmatrix} p_0 \cr p_1 \cr p_2 \cr \vdots \cr p_{T-1} \cr p_T \end{bmatrix} = \begin{bmatrix} d_0 \cr d_1 \cr d_2 \cr \vdots \cr d_{T-1} \cr d_T \end{bmatrix} + \begin{bmatrix} 0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr \delta p_{T+1}^* \end{bmatrix} \]

Exercise 11.1

手动用矩阵乘法对(11.3)进行计算，然后用 (11.2)确认。

用向量-矩阵表示法，我们可以将系统(11.3)写成

(11.4)\[ A p = d + b \]

这里\(A\)是方程(11.3)左侧的矩阵，而

\[\begin{split} p = \begin{bmatrix} p_0 \\ p_1 \\ \vdots \\ p_T \end{bmatrix}, \quad d = \begin{bmatrix} d_0 \\ d_1 \\ \vdots \\ d_T \end{bmatrix}, \quad \text{and} \quad b = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ p^*_{T+1} \end{bmatrix} \end{split}\]

价格向量的解是

(11.5)\[ p = A^{-1}(d + b) \]

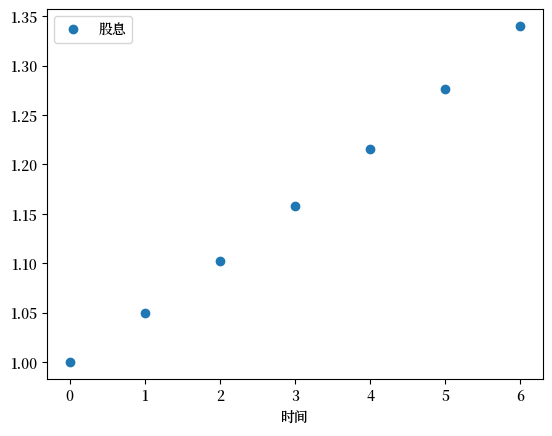
例如，假设股息流是

\[ d_{t+1} = 1.05 d_t, \quad t = 0, 1, \ldots , T-1. \]

让我们编写Python代码来计算和绘制股息流。

import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

T = 6
current_d = 1.0
d = []
for t in range(T+1):
    d.append(current_d)
    current_d = current_d * 1.05 

fig, ax = plt.subplots()
ax.plot(d, 'o', label='股息')
ax.legend()
ax.set_xlabel('时间')
plt.show()

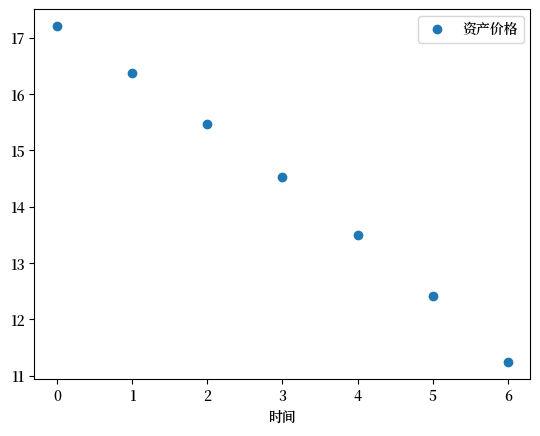
现在让我们来计算和绘制资产价格。

我们将 \(\delta\) 和 \(p_{T+1}^*\) 设定为

δ = 0.99
p_star = 10.0

现在我们建立矩阵 \(A\)

A = np.zeros((T+1, T+1))
for i in range(T+1):
    for j in range(T+1):
        if i == j:
            A[i, j] = 1
            if j < T:
                A[i, j+1] = -δ

让我们将矩阵 \(A\) 打印出来：

A

array([[ 1.  , -0.99,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  1.  , -0.99,  0.  ,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  1.  , -0.99,  0.  ,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  1.  , -0.99,  0.  ,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  1.  , -0.99,  0.  ],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  1.  , -0.99],
       [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  0.  ,  1.  ]])

现在用 (11.5)来求解价格。

b = np.zeros(T+1)
b[-1] = δ * p_star
p = np.linalg.solve(A, d + b)
fig, ax = plt.subplots()
ax.plot(p, 'o', label='资产价格')
ax.legend()
ax.set_xlabel('时间')
plt.show()

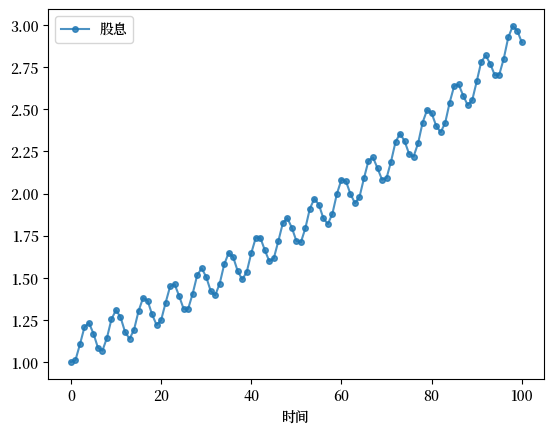
现在让我们考虑一个周期性增长的股息序列：

\[ d_{t+1} = 1.01 d_t + 0.1 \sin t, \quad t = 0, 1, \ldots , T-1. \]

T = 100
current_d = 1.0
d = []
for t in range(T+1):
    d.append(current_d)
    current_d = current_d * 1.01 + 0.1 * np.sin(t)

fig, ax = plt.subplots()
ax.plot(d, 'o-', ms=4, alpha=0.8, label='股息')
ax.legend()
ax.set_xlabel('时间')
plt.show()

Exercise 11.2

当\(p^*_{T+1} = 0\) 和 \(\delta = 0.98\) 时，计算相对应的价格序列。

Solution to Exercise 11.2

我们改变之前的参数和矩阵\(A\)。

δ = 0.98
p_star = 0.0
A = np.zeros((T+1, T+1))
for i in range(T+1):
    for j in range(T+1):
        if i == j:
            A[i, j] = 1
            if j < T:
                A[i, j+1] = -δ

b = np.zeros(T+1)
b[-1] = δ * p_star
p = np.linalg.solve(A, d + b)
fig, ax = plt.subplots()
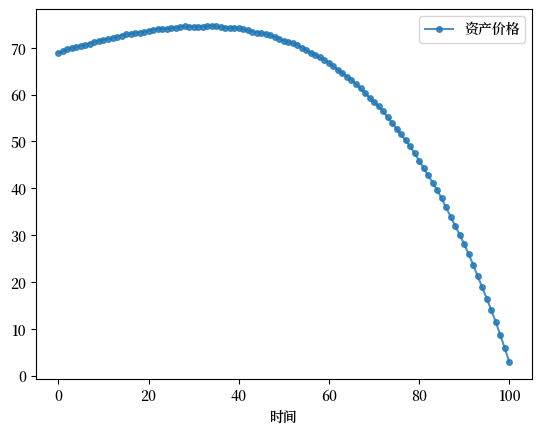
ax.plot(p, 'o-', ms=4, alpha=0.8, label='资产价格')
ax.legend()
ax.set_xlabel('时间')
plt.show()

与现值计算相关的加权平均在很大程度上消除了周期。

11.4. 解析表达式

根据逆矩阵定理，当\(A B\)是单位矩阵时，矩阵\(B\)是\(A\)的逆矩阵。

可以验证，(11.3)中的矩阵\(A\)的逆矩阵是

(11.6)\[ A^{-1} = \begin{bmatrix} 1 & \delta & \delta^2 & \cdots & \delta^{T-1} & \delta^T \cr 0 & 1 & \delta & \cdots & \delta^{T-2} & \delta^{T-1} \cr \vdots & \vdots & \vdots & \cdots & \vdots & \vdots \cr 0 & 0 & 0 & \cdots & 1 & \delta \cr 0 & 0 & 0 & \cdots & 0 & 1 \cr \end{bmatrix} \]

Exercise 11.3

通过证明\(AA^{-1}\)为单位矩阵来验证这一点。

如果我们在 (11.5) 中使用表达式 (11.6) 并执行所指示的矩阵乘法，我们将发现

(11.7)\[ p_t = \sum_{s=t}^T \delta^{s-t} d_s + \delta^{T+1-t} p_{T+1}^* \]

定价公式 (11.7) 表明资产价格 \(p_t\) 由两个组成部分相加得到：

• 基本面部分 \(\sum_{s=t}^T \delta^{s-t} d_s\)，它等于预期股息的贴现现值

• 泡沫组成部分 \(\delta^{T+1-t} p_{T+1}^*\)

基本组成部分由贴现因子 \(\delta\) 和资产的支付（在这种情况下为股息）确定。

泡沫组成部分是其中不由基本面决定的价格部分。

有时将泡沫组成部分重写为

\[ c \delta^{-t} \]

更为方便，其中

\[ c \equiv \delta^{T+1}p_{T+1}^* \]

11.5. 关于泡沫的更多内容

让我们暂时考虑一个从不支付股息的资产这个特殊情况，在这种情况下

\[ \begin{bmatrix} d_0 \cr d_1 \cr d_2 \cr \vdots \cr d_{T-1} \cr d_T \end{bmatrix} = \begin{bmatrix} 0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr 0 \end{bmatrix} \]

在这种情况下，我们的 \(T+1\) 资产定价方程系统 (11.1) 采用以下单一矩阵方程的形式：

(11.8)\[ \begin{bmatrix} 1 & -\delta & 0 & 0 & \cdots & 0 & 0 \cr 0 & 1 & -\delta & 0 & \cdots & 0 & 0 \cr 0 & 0 & 1 & -\delta & \cdots & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & 0 & 0 \cr 0 & 0 & 0 & 0 & \cdots & 1 & -\delta \cr 0 & 0 & 0 & 0 & \cdots & 0 & 1 \end{bmatrix} \begin{bmatrix} p_0 \cr p_1 \cr p_2 \cr \vdots \cr p_{T-1} \cr p_T \end{bmatrix} = \begin{bmatrix} 0 \cr 0 \cr 0 \cr \vdots \cr 0 \cr \delta p_{T+1}^* \end{bmatrix} \]

显然，如果 \(p_{T+1}^* = 0\)，一个所有元素为零的价格向量 \(p\) 可以解这个方程，此时我们定价公式 (11.7) 中只有基本面成分存在。

但让我们通过设置以下条件来激活泡沫成分：

(11.9)\[ p_{T+1}^* = c \delta^{-(T+1)} \]

其中 \(c\) 为某个正数。

在这种情况下，当我们用方程 (11.6) 中的矩阵 \(A^{-1}\) 乘以 (11.8) 的两边时，我们发现：

(11.10)\[ p_t = c \delta^{-t} \]

11.6. 总回报率

定义从 \(t\) 期到 \(t+1\) 期持有资产的总回报率为：

(11.11)\[ R_t = \frac{p_{t+1}}{p_t} \]

将方程 (11.10) 代入方程 (11.11) 可以确认，一个价值完全来源于泡沫的资产的总回报率为：

\[ R_t = \delta^{-1} > 1 , t = 0, 1, \ldots, T \]

11.7. 练习

Exercise 11.4

给出以下 \(d\) 和 \(p_{T+1}^*\) 设置下资产价格 \(p_t\) 的分析表达式：

1. \(p_{T+1}^* = 0, d_t = g^t d_0\)（戈登增长公式的修改版）

2. \(p_{T+1}^* = g^{T+1} d_0, d_t = g^t d_0\)（普通的戈登增长公式）

3. \(p_{T+1}^* = 0, d_t = 0\)（一个无价值股票的价格）

4. \(p_{T+1}^* = c \delta^{-(T+1)}, d_t = 0\)（一个纯泡沫股票的价格）

Solution to Exercise 11.4

将上述每对 \(p_{T+1}^*, d_t\) 代入方程 (11.7) 得到：

1. \(p_t = \sum^T_{s=t} \delta^{s-t} g^s d_0\)

2. \(p_t = \sum^T_{s=t} \delta^{s-t} g^s d_0 + \delta^{T+1-t} g^{T+1} d_0\)

3. \(p_t = 0\)

4. \(p_t = c \delta^{-t}\)