45. 最大似然估计#

from scipy.stats import lognorm, pareto, expon
import numpy as np
from scipy.integrate import quad
import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
from math import exp

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

45.1. 介绍#

假设你是一位政策制定者，你想尝试估算增加财富税将带来多少收入。

财富税的计算公式为：

\begin{array}{r} h (w) = {\begin{cases} a w & if w \leq \bar{w} \\ a \bar{w} + b (w - \bar{w}) & if w > \bar{w} \end{cases} \end{array}

其中 $w$ 代表财富。

Example 45.1

例如，如果 $a = 0.05$ ， $b = 0.1$ ，且 $\bar{w} = 2.5$ ，意味着：

对于2.5及以下的财富征收5%的税，
对超过2.5的部分征收10%的税。

这里财富的单位是100,000，所以 $w = 2.5$ 指 250,000 美元。

接下来，我们定义函数 $h$ :

def h(w, a=0.05, b=0.1, w_bar=2.5):
    if w <= w_bar:
        return a * w
    else:
        return a * w_bar + b * (w - w_bar)

对于一个人口数量为 $N$ 的地区，每个人 $i$ 拥有财富 $w_{i}$ ，则财富税收入总额为

T = \sum_{i = 1}^{N} h (w_{i})

而我们希望计算这一数量。

但问题是，在大多数国家中，并不是所有的个人财富都能被观测到。

收集并追踪一国所有个人或家庭的财富数据是非常困难的。

因此，假设我们得到了一个样本 $w_{1}, w_{2}, \dots, w_{n}$ ，它包含了 $n$ 位随机选择的个人的财富。

在练习中，我们将使用 $n = 10, 000$ 来自2016年美国的财富数据样本。

n = 10_000

这些数据来源于消费者财务状况调查 (SCF)。

以下代码导入了数据并将其读入名为 sample 的数组。

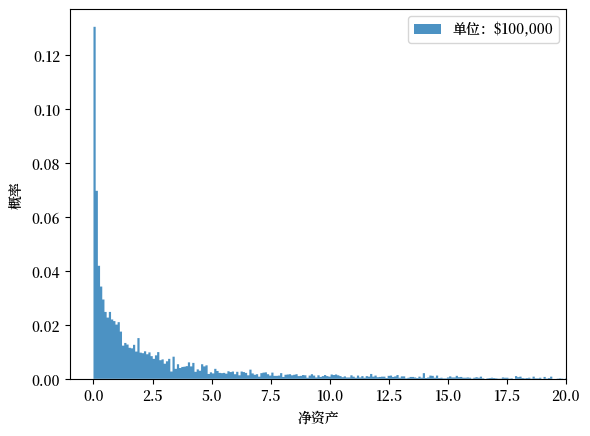
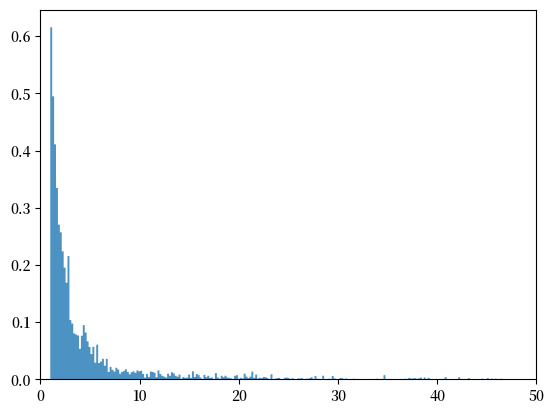
我们先绘制该样本的直方图。

fig, ax = plt.subplots()
ax.set_xlim(-1, 20)
density, edges = np.histogram(sample, bins=5000, density=True)
prob = density * np.diff(edges)
plt.stairs(prob, edges, fill=True, alpha=0.8, label=r"单位：\$100,000")
plt.ylabel("概率")
plt.xlabel("净资产")
plt.legend()
plt.show()

_images/600e59ebb2cb93513e98499e7e888a2ff4a33bcc8c7afc442422d3bbae6d5bf3.png

该直方图显示，大部分人的财富水平很低，而少部分人却拥有非常多的财富。

我们假定全体人口规模为

N = 100_000_000

仅依靠样本数据，我们又该如何估计全体人口的总收入呢？

我们的计划是，假设每个人的财富是从密度为 $f$ 的分布中抽取的。

如果我们获得 $f$ 的估计，那么我们可以按照以下方式近似 $T$ ：

(45.1)#

T = \sum_{i = 1}^{N} h (w_{i}) = N \frac{1}{N} \sum_{i = 1}^{N} h (w_{i}) \approx N \int_{0}^{\infty} h (w) f (w) d w

（根据大数定律，样本均值应该接近总体均值。）

现在的问题是：我们要如何估计 $f$ ？

45.2. 最大似然估计#

最大似然估计是一种估计未知分布的方法。

最大似然估计有两个步骤：

猜测潜在分布是什么（例如，均值为 $μ$ ，标准差为 $σ$ 的正态分布）。
估计参数值（例如，估计正态分布的 $μ$ 和 $σ$ ）。

对于财富而言，一种假设是每个 $w_{i}$ 都符合对数正态分布的，其中参数 $μ \in (- \infty, \infty)$ ， $σ \in (0, \infty)$ 。

（这意味着 $\ln w_{i}$ 是以 $μ$ 为均值， $σ$ 为标准差的正态分布。）

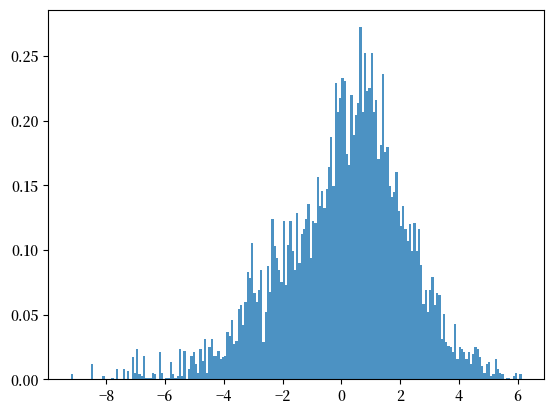
不难发现，这个假设不是完全没有道理，因为如果我们用直方图表示财富的对数（而不是财富本身），直方图将看起来像一个钟形曲线。

ln_sample = np.log(sample)
fig, ax = plt.subplots()
ax.hist(ln_sample, density=True, bins=200, histtype='stepfilled', alpha=0.8)
plt.show()

_images/cc021dc1a8103f4be234ad8e70c7ee059c14302381c89a8c0380564f46bfdc27.png

我们现在的任务是获取 $μ$ 和 $σ$ 的最大似然估计值，我们用 $\hat{μ}$ 和 $\hat{σ}$ 表示。

这些估计值可以通过最大化给定数据的似然函数获得。

对数正态分布随机变量 $X$ 的概率密度函数 (PDF) 如下：

f (x, μ, σ) = \frac{1}{x} \frac{1}{σ \sqrt{2 π}} \exp (- \frac{1}{2} {(\frac{\ln x - μ}{σ})}^{2})

对于我们的样本 $w_{1}, w_{2}, \dots, w_{n}$ ，似然函数是：

L (μ, σ | w_{i}) = \prod_{i = 1}^{n} f (w_{i}, μ, σ)

似然函数可以被视为：

样本（假设是独立同分布）的联合分布和
给定数据的参数 $(μ, σ)$ 的“似然性”。

对两边取对数，我们得到对数似然函数：

\begin{array}{r} \begin{aligned} ℓ (μ, σ | w_{i}) & = \ln [\prod_{i = 1}^{n} f (w_{i}, μ, σ)] \\ = - \sum_{i = 1}^{n} \ln w_{i} - \frac{n}{2} \ln (2 π) - \frac{n}{2} \ln σ^{2} - \frac{1}{2 σ^{2}} \sum_{i = 1}^{n} (\ln w_{i} - μ)^{2} \end{aligned} \end{array}

要找到这个函数的最大值，我们需要计算对 $μ$ 和 $σ^{2}$ 的偏导数，并令结果为 $0$ .

我们首先推导 $μ$ 的最大似然估计（MLE）

\begin{array}{r} \frac{δ ℓ}{δ μ} = - \frac{1}{2 σ^{2}} \times 2 \sum_{i = 1}^{n} (\ln w_{i} - μ) = 0 \\ ⟹ \sum_{i = 1}^{n} \ln w_{i} - n μ = 0 \\ ⟹ \hat{μ} = \frac{\sum_{i = 1}^{n} \ln w_{i}}{n} \end{array}

现在让我们推导 $σ$ 的最大似然估计

\begin{array}{r} \frac{δ ℓ}{δ σ^{2}} = - \frac{n}{2 σ^{2}} + \frac{1}{2 σ^{4}} \sum_{i = 1}^{n} (\ln w_{i} - μ)^{2} = 0 \\ ⟹ \frac{n}{2 σ^{2}} = \frac{1}{2 σ^{4}} \sum_{i = 1}^{n} (\ln w_{i} - μ)^{2} \\ ⟹ \hat{σ} = {(\frac{\sum_{i = 1}^{n} (\ln w_{i} - \hat{μ})^{2}}{n})}^{1 / 2} \end{array}

至此我们已经推导出 $\hat{μ}$ 和 $\hat{σ}$ 的表达式，现在要通过财富样本计算具体数值。

μ_hat = np.mean(ln_sample) # 计算 μ 的估计值
μ_hat

0.0634375526654064

num = (ln_sample - μ_hat)**2 # 计算方差的分子
σ_hat = (np.mean(num))**(1/2) # 计算 σ 的估计值
σ_hat

2.1507346258433424

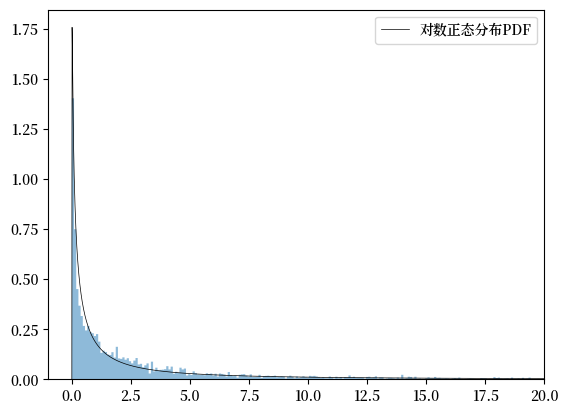
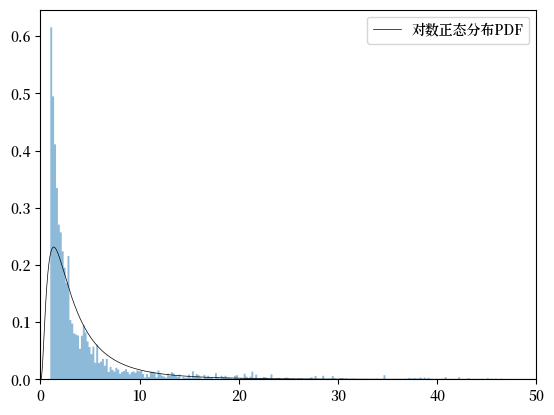
我们绘制对数正态分布概率密度函数（使用估计的参数），并与样本数据进行对比。

dist_lognorm = lognorm(σ_hat, scale = exp(μ_hat))  # 初始化对数正态分布
x = np.linspace(0,50,10000)  # 产生数据点

fig, ax = plt.subplots()  # 创建图形和轴
ax.set_xlim(-1,20)  # 设置x轴的范围

ax.hist(sample, density=True, bins=5_000, histtype='stepfilled', alpha=0.5)  # 绘制样本的直方图
ax.plot(x, dist_lognorm.pdf(x), 'k-', lw=0.5, label='对数正态分布PDF')  # 绘制对数正态分布的PDF
ax.legend()  # 显示图例
plt.show()  # 展示图形

_images/c300c57991ed03f10356dc41768f74d3de5179f13fd8f4a16e2033f31a3af166.png

我们估计的对数正态分布看起来很适合整体数据。

我们现在使用方程(45.1)来计算总收入。

我们将通过 SciPy 的 quad 函数，使用数值积分的方式计算积分。

def total_revenue(dist):
    integral, _ = quad(lambda x: h(x) * dist.pdf(x), 0, 100_000)  # 计算积分
    T = N * integral  # 总收入 = 人数 * 单个收入
    return T  # 返回总收入

tr_lognorm = total_revenue(dist_lognorm)  # 使用对数正态分布计算总收入
tr_lognorm  # 显示总收入

101105326.82814859

（我们的单位是10万美元，这意味着实际收入是这一数字的10万倍。）

45.3. 帕累托分布#

如上所示，使用最大似然估计时，我们需要先对分布做出假设。

刚才我们假定这个分布是对数正态分布。

如果，我们改为假设 $w_{i}$ 抽样自参数为 $b$ 和 $x_{m}$ 的帕累托分布。

在这种情况下，最大似然估计为

\hat{b} = \frac{n}{\sum_{i = 1}^{n} \ln (w_{i} / \hat{x_{m}})} 和 {\hat{x}}_{m} = min_{i} w_{i}

下面，我们来计算它们。

xm_hat = min(sample)
xm_hat

0.0001

den = np.log(sample/xm_hat)
b_hat = 1/np.mean(den)
b_hat

0.10783091940803055

现在让我们重新计算总收入。

dist_pareto = pareto(b = b_hat, scale = xm_hat)
tr_pareto = total_revenue(dist_pareto) 
tr_pareto

12933168365.762571

这个数字差别很大！

tr_pareto / tr_lognorm

127.91777418162567

可见，选择正确的分布极其重要。

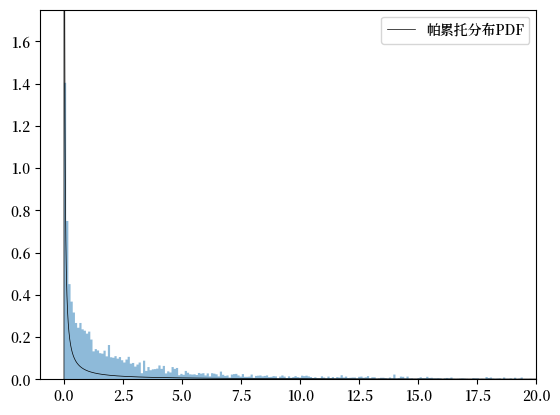
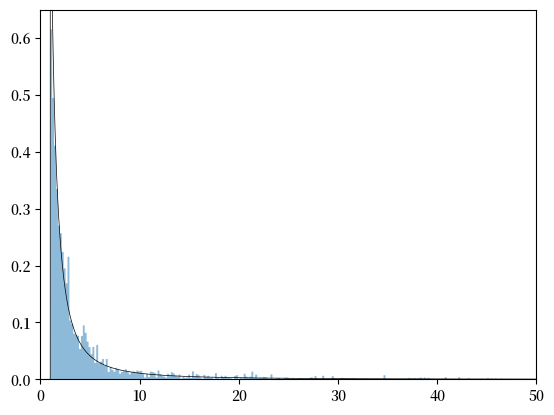
我们将拟合的帕累托分布与直方图进行比较：

fig, ax = plt.subplots()
ax.set_xlim(-1, 20)
ax.set_ylim(0,1.75)

ax.hist(sample, density=True, bins=5_000, histtype='stepfilled', alpha=0.5)
ax.plot(x, dist_pareto.pdf(x), 'k-', lw=0.5, label='帕累托分布PDF')
ax.legend()

plt.show()

_images/b164aa38fbd667d4d79645490902a9328d6099a9db642c2ea93f7cf274724cae.png

我们观察到在这种情况下，帕累托分布的拟合效果并不理想，所以我们很可能会拒绝这一假设。

45.4. 最好的分布是怎样的？#

没有“最好”的分布——我们做出的每一个选择，都只是一种假设。

我们唯一能做的，就是不断尝试，选择一个能很好拟合数据的分布。

上面的图表表明，对数正态分布是最佳的。

然而，当我们检查右尾部（最富有的人）时，帕累托分布可能是一个更好的选择。

要看清楚这一点，让我们设定数据集中净资产最低阈值。

我们不妨设定阈值为 $500,000，并将数据读入 sample_tail。

接下来，绘制这些数据。

fig, ax = plt.subplots()
ax.set_xlim(0,50)
ax.hist(sample_tail, density=True, bins=500, histtype='stepfilled', alpha=0.8)
plt.show()

_images/c4baf6cd7deaaaee43574b48d1da81a16db5267feecd347ac9d26cc5d6b6e4bc.png

现在，我们尝试用不同的分布来拟合数据。

45.4.1. 用对数正态分布拟合右尾部#

让我们从对数正态分布开始。

我们重新估计参数并绘制概率密度函数，与数据进行对比。

ln_sample_tail = np.log(sample_tail)
μ_hat_tail = np.mean(ln_sample_tail)
num_tail = (ln_sample_tail - μ_hat_tail)**2
σ_hat_tail = (np.mean(num_tail))**(1/2)
dist_lognorm_tail = lognorm(σ_hat_tail, scale = exp(μ_hat_tail))

fig, ax = plt.subplots()
ax.set_xlim(0,50)
ax.hist(sample_tail, density=True, bins=500, histtype='stepfilled', alpha=0.5)
ax.plot(x, dist_lognorm_tail.pdf(x), 'k-', lw=0.5, label='对数正态分布PDF')
ax.legend()
plt.show()

_images/5fb557a155c1e076bf0839f6458eb1017d5e361341b58aa9f276d51070b0142d.png

虽然对数正态分布对整个数据集拟合良好，但它对于右尾部的拟合效果并不好。

45.4.2. 用帕累托分布拟合右尾部#

现在假设截取的数据集符合帕累托分布。

我们再次估计参数，并将概率密度函数与数据进行对比。

xm_hat_tail = min(sample_tail)
den_tail = np.log(sample_tail/xm_hat_tail)
b_hat_tail = 1/np.mean(den_tail)
dist_pareto_tail = pareto(b = b_hat_tail, scale = xm_hat_tail)

fig, ax = plt.subplots()
ax.set_xlim(0, 50)
ax.set_ylim(0,0.65)
ax.hist(sample_tail, density=True, bins= 500, histtype='stepfilled', alpha=0.5)
ax.plot(x, dist_pareto_tail.pdf(x), 'k-', lw=0.5, label='帕累托分布PDF')
plt.show()

_images/f899ac0764a8f7929bcefae0ce359069e0d054231c2957b30c6520a6cd63512b.png

帕累托分布更适合数据集的右尾部。

45.4.3. 到底什么才是最好的分布？#

如刚才所言，没有“最好”的分布——每个选择都只是一种假设。

我们只需要检验我们认为合理的分布。

一种检验方法是，将数据与拟合分布进行绘图，如我们刚才所做的。

还有其他更严谨的测试方法，比如科尔莫格罗夫一斯米尔诺夫拟合优度检验。

我们省略了这些更深入的主题（但我们鼓励读者在完成这些讲座后研究它们）。

45.5. 练习#

Exercise 45.1

假设我们假设财富是以参数 $λ > 0$ 的指数分布。

$λ$ 的最大似然估计为

\hat{λ} = \frac{n}{\sum_{i = 1}^{n} w_{i}}

计算我们初始样本的 $\hat{λ}$ 。
使用 $\hat{λ}$ 来计算总收入

Solution to Exercise 45.1

λ_hat = 1/np.mean(sample)
λ_hat

0.15234120963403971

dist_exp = expon(scale = 1/λ_hat)
tr_expo = total_revenue(dist_exp) 
tr_expo

55246978.53427645

Exercise 45.2

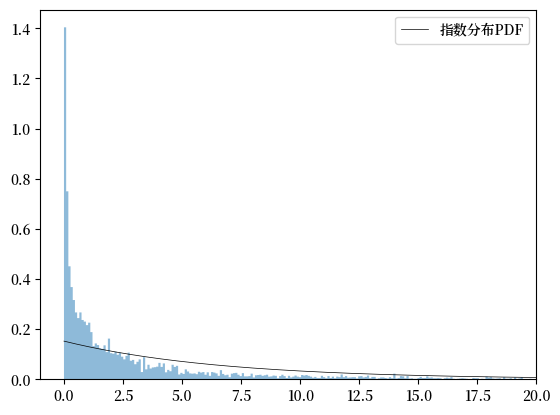
绘制指数分布曲线，与样本比较并讨论它的拟合效果。

Solution to Exercise 45.2

fig, ax = plt.subplots()
ax.set_xlim(-1, 20)

ax.hist(sample, density=True, bins=5000, histtype='stepfilled', alpha=0.5)
ax.plot(x, dist_exp.pdf(x), 'k-', lw=0.5, label='指数分布PDF')
ax.legend()

plt.show()

_images/448fcc6a5c448e9ff95739edf248e13ff47116ef579f5c8f29ebf9070d0c4c29.png

显然，这个分布对数据的拟合效果并不好。