31. 拉弗曲线与自适应预期#

31.1. 概览#

本讲座研究了在通货膨胀税率下的静态和动态拉弗曲线，其采用的模型为此讲座通过货币资助的政府赤字和价格水平中研究的非线性版本。

与讲座通过货币资助的政府赤字和价格水平中一样，此讲座使用了[Cagan, 1956]在其经典论文中使用的对数线性货币需求函数版本，而不是此讲座通过货币资助的政府赤字和价格水平中使用的线性需求函数。

但在本讲中，我们将不采用”理性预期”的”完全预见”形式，而是采用[Cagan, 1956]和[Friedman, 1956]使用的”自适应预期”假设。

这意味着，我们不再假设预期通货膨胀 $π_{t}^{*}$ 遵循”完全预见”或”理性预期”

π_{t}^{*} = p_{t + 1} - p_{t}

我们现在不再采用讲座通过货币资助的政府赤字和价格水平和讲座通货膨胀税的拉弗曲线中的假设，而是假设 $π_{t}^{*}$ 遵循下文中的自适应预期假设(31.4)。

这种预期形成机制的改变会带来一些重要的影响。具体来说:

两个静态通货膨胀率水平保持不变
但系统的动态行为发生了变化 - 它现在倾向于收敛到较低的通货膨胀率水平
政策效果变得更符合直觉 - 降低政府赤字能够降低通货膨胀

这些结果更符合传统的经济学观点,即通货膨胀主要由政府赤字驱动。

[Bruno and Fischer, 1990]对这些问题进行了研究。他们认为理性预期(完全预见)模型的预测有悖直觉,因此提出用自适应预期来替代。在自适应预期下,人们根据下文的方程(31.4)来形成对未来通货膨胀的预期。

Note

[Marcet and Sargent, 1989] 研究了另一种选择静态均衡的方法，涉及用通过最小二乘回归学习的模型替换理性预期。 [Marcet and Nicolini, 2003] 和 [Sargent et al., 2009] 扩展了这项工作，并将其应用于研究拉丁美洲反复出现的高通胀情节。

31.2. 模型#

设

$m_{t}$ 为时间 $t$ 初始的货币供应量对数
$p_{t}$ 为时间 $t$ 的价格水平对数
$π_{t}^{*}$ 为公众对于时间 $t$ 到 $t + 1$ 之间的通胀率的预期

货币供应量的动态方程是

(31.1)#

\exp (m_{t + 1}) - \exp (m_{t}) = g \exp (p_{t})

其中 $g$ 是政府支出中通过印制货币来融资的部分。

注意方程 (31.1) 暗示

(31.2)#

m_{t + 1} = \log [\exp (m_{t}) + g \exp (p_{t})]

货币需求函数是

(31.3)#

m_{t + 1} - p_{t} = - α π_{t}^{*}

其中 $α \geq 0$ 。

通胀预期受控于

(31.4)#

π_{t}^{*} = (1 - δ) (p_{t} - p_{t - 1}) + δ π_{t - 1}^{*}

其中 $δ \in (0, 1)$

31.3. 计算均衡序列#

我们可以通过以下步骤求解均衡序列。首先，将方程(31.3)和(31.2)中的 $m_{t + 1}$ 表达式结合，并使用方程(31.4)消除 $π_{t}^{*}$ ，得到关于 $p_{t}$ 的方程：

(31.5)#

\log [\exp (m_{t}) + g \exp (p_{t})] - p_{t} = - α [(1 - δ) (p_{t} - p_{t - 1}) + δ π_{t - 1}^{*}]

给定初始条件 $(m_{0}, π_{- 1}^{*}, p_{- 1})$ ，我们可以按照以下步骤求解均衡序列：

求解方程(31.5)得到 $p_{t}$
使用方程(31.4)计算 $π_{t}^{*}$
使用方程(31.2)计算 $m_{t + 1}$
重复步骤1-3

31.4. 主要结论#

通过分析模型,我们可以得出以下几个重要结论:

如果存在稳态,通货膨胀率 $\overset{―}{π}$ 将等于货币增长率 $\overset{―}{μ}$
模型存在两个可能的稳态通货膨胀率 - 一个高值和一个低值
与通货膨胀税的拉弗曲线中的理性预期模型不同,在大多数初始条件 $(p_{0}, π_{t}^{*})$ 下,系统会收敛到较低的稳态通货膨胀率
对于每个稳态通货膨胀率 $\overset{―}{π}$ ,都存在唯一的初始价格水平 $p_{0}$ 使得系统立即进入稳态( $π_{t} = μ_{t} = \overset{―}{μ}$ 对所有 $t \geq 0$ )
- 这个 $p_{0}$ 满足方程: $\log (\exp (m_{0}) + g \exp (p_{0})) - p_{0} = - α \overset{―}{π}$
- 该方程来自稳态条件 $m_{1} - p_{0} = - α \overset{―}{π}$

31.5. 稳态通货膨胀率的计算#

正如我们在早前的讲座通货膨胀税的拉弗曲线中讨论的，我们可以通过研究稳态劳动曲线来计算 $\bar{π}$ 的两个潜在的限制值。

因此，在一个稳态中 $ $m_{t + 1} - m_{t} = p_{t + 1} - p_{t} = x \forall t,$ $

其中 $x > 0$ 是货币供应量和价格水平的对数的共同增长率。

几行代数可以得出满足 $x$ 的以下方程

(31.6)#

\exp (- α x) - \exp (- (1 + α) x) = g

我们需要满足

(31.7)#

g \leq max_{x : x \geq 0} \exp (- α x) - \exp (- (1 + α) x),

这样就可以通过印钞来财务支持 $g$ 。

(31.6) 的左侧是通过印钞筹集的稳定状态收入。

(31.6) 的右侧是政府通过印钞筹集的 $t$ 时刻的商品数量。

很快我们将绘制方程 (31.6) 的左右两侧。

但首先，我们将编写代码来计算稳态的 $\bar{π}$ 。

让我们开始导入一些库

from collections import namedtuple
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib.ticker import MaxNLocator
from matplotlib.cm import get_cmap
from matplotlib.colors import to_rgba
import matplotlib
from scipy.optimize import root, fsolve

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

让我们创建一个 namedtuple 来存储模型的参数

LafferAdaptive = namedtuple('LafferAdaptive', 
                        ["m0",  # t=0时货币供应量的对数
                         "α",   # 货币需求的敏感性
                         "g",   # 政府支出
                         "δ"])

# 创建一个 凯根拉弗 模型 
def create_model(α=0.5, m0=np.log(100), g=0.35, δ=0.9):
    return LafferAdaptive(α=α, m0=m0, g=g, δ=δ)

model = create_model()

现在我们编写计算稳态 $\bar{π}$ 的代码。

# 定义 π_bar 的计算公式
def solve_π(x, α, g):
    return np.exp(-α * x) - np.exp(-(1 + α) * x) - g

def solve_π_bar(model, x0):
    π_bar = fsolve(solve_π, x0=x0, xtol=1e-10, args=(model.α, model.g))[0]
    return π_bar

# 解两个稳态的 π
π_l = solve_π_bar(model, x0=0.6)
π_u = solve_π_bar(model, x0=3.0)
print(f'两个稳态的π是: {π_l, π_u}')

两个稳态的π是: (0.6737147075333032, 1.6930797322614812)

我们找到了两个稳态 $\bar{π}$ 值。

31.6. 稳态拉弗曲线#

下图绘制了稳态拉弗曲线以及两个稳定的通货膨胀率。

def compute_seign(x, α):
    return np.exp(-α * x) - np.exp(-(1 + α) * x) 

def plot_laffer(model, πs):
    α, g = model.α, model.g
    
    # 生成π值
    x_values = np.linspace(0, 5, 1000)

    # 计算对应的铸币税值
    y_values = compute_seign(x_values, α)

    # 绘制函数图形
    plt.plot(x_values, y_values, 
            label=f'$exp((-{α})x) - exp(- (1- {α}) x)$')
    for π, label in zip(πs, [r'$\pi_l$', r'$\pi_u$']):
        plt.text(π, plt.gca().get_ylim()[0]*2, 
                 label, horizontalalignment='center',
                 color='brown', size=10)
        plt.axvline(π, color='brown', linestyle='--')
    plt.axhline(g, color='red', linewidth=0.5, 
                linestyle='--', label='g')
    plt.xlabel(r'$\pi$')
    plt.ylabel('铸币税')
    plt.legend()
    plt.grid(True)
    plt.show()

# 稳态拉弗曲线
plot_laffer(model, (π_l, π_u))

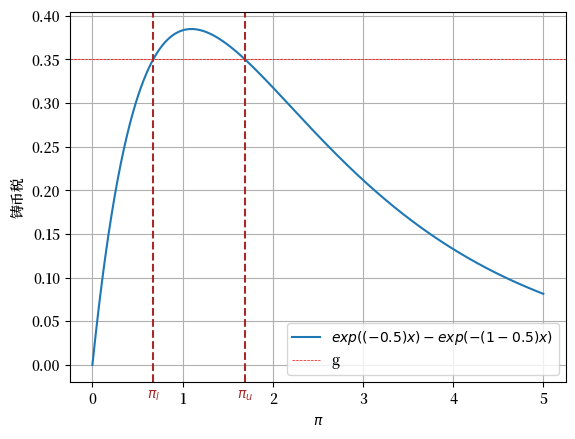
_images/a76632c39d8d60d939eb5fe083173d0bab423d173c818b495c505e73f9a93e16.png — Fig. 31.1 稳态通胀下的铸币税函数。棕色虚线代表 $π_{l}$ 和 $π_{u}$ 。#

31.7. 初始价格水平的计算#

既然我们已经找到了两个可能的稳态通货膨胀率，接下来我们需要计算与每个稳态相对应的初始价格水平 $p_{- 1}$ 。

这些初始价格水平很重要，因为它们能让系统从一开始就处于稳态，也就是说，如果我们从正确的 $p_{- 1}$ 开始，那么通货膨胀率 $π_{t}$ 会在所有时期 $t \geq 0$ 保持在稳态值 $\bar{π}$ 不变。

根据货币需求方程，初始价格水平应满足:

p_{- 1} = m_{0} + α π^{*}

其中 $m_{0}$ 是初始货币供应量的对数， $α$ 是货币需求对预期通货膨胀的敏感度， $π^{*}$ 是稳态通货膨胀率。

def solve_p_init(model, π_star):
    m0, α = model.m0, model.α
    return m0 + α*π_star

# 计算与 π_l 和 π_u 相关联的两个初始价格水平
p_l, p_u = map(lambda π: solve_p_init(model, π), (π_l, π_u))
print('初始 p_{-1}', f'为: {p_l, p_u}')

初始 p_{-1} 为: (4.9420275397547435, 5.451710052118832)

31.7.1. 验证#

首先，我们编写一些代码来验证，如果我们适当初始化 $π_{- 1}^{*}, p_{- 1}$ ，则通货膨胀率 $π_{t}$ 对于所有 $t \geq 0$ 将保持恒定（根据初始条件的不同，可能是较高的稳态值 $π_{u}$ 或较低的稳态值 $π_{l}$ ）。

以下代码进行了验证。

def solve_laffer_adapt(p_init, π_init, model, num_steps):
    m0, α, δ, g = model.m0, model.α, model.δ, model.g
    
    m_seq = np.nan * np.ones(num_steps+1) 
    π_seq = np.nan * np.ones(num_steps) 
    p_seq = np.nan * np.ones(num_steps)
    μ_seq = np.nan * np.ones(num_steps) 
    
    m_seq[1] = m0
    π_seq[0] = π_init
    p_seq[0] = p_init
        
    for t in range(1, num_steps):
        # 解出 p_t
        def p_t(pt):
            return np.log(np.exp(m_seq[t]) + g * np.exp(pt)) - pt + α * ((1-δ)*(pt - p_seq[t-1]) + δ*π_seq[t-1])
        
        p_seq[t] = root(fun=p_t, x0=p_seq[t-1]).x[0]
        
        # 解出 π_t
        π_seq[t] = (1-δ) * (p_seq[t]-p_seq[t-1]) + δ*π_seq[t-1]
        
        # 解出 m_t
        m_seq[t+1] = np.log(np.exp(m_seq[t]) + g*np.exp(p_seq[t]))
        
        # 解出 μ_t
        μ_seq[t] = m_seq[t+1] - m_seq[t]
    
    return π_seq, μ_seq, m_seq, p_seq

计算从 $p_{- 1}$ 开始，与 $π_{l}$ 相关联的极限值

π_seq, μ_seq, m_seq, p_seq = solve_laffer_adapt(p_l, π_l, model, 50)

# 检查稳态 m_{t+1} - m_t 和 p_{t+1} - p_t
print('m_{t+1} - m_t:', m_seq[-1] - m_seq[-2])
print('p_{t+1} - p_t:', p_seq[-1] - p_seq[-2])

# 检查 exp(-αx) - exp(-(1 + α)x) 是否等于 g
eq_g = lambda x: np.exp(-model.α * x) - np.exp(-(1 + model.α) * x)

print('eq_g == g:', np.isclose(eq_g(m_seq[-1] - m_seq[-2]), model.g))

m_{t+1} - m_t: 0.6737147075332999
p_{t+1} - p_t: 0.6737147075332928
eq_g == g: True

现在计算从初始价格水平 $p_{- 1}$ 开始，收敛到高通胀稳态 $π_{u}$ 的动态路径

π_seq, μ_seq, m_seq, p_seq = solve_laffer_adapt(p_u, π_u, model, 50)

# 检查稳态 m_{t+1} - m_t 和 p_{t+1} - p_t
print('m_{t+1} - m_t:', m_seq[-1] - m_seq[-2])
print('p_{t+1} - p_t:', p_seq[-1] - p_seq[-2])

# 检查 exp(-αx) - exp(-(1 + α)x) 是否等于 g
eq_g = lambda x: np.exp(-model.α * x) - np.exp(-(1 + model.α) * x)

print('eq_g == g:', np.isclose(eq_g(m_seq[-1] - m_seq[-2]), model.g))

m_{t+1} - m_t: 1.69307973225105
p_{t+1} - p_t: 1.6930797322506947
eq_g == g: True

31.8. 拉弗曲线动态的不稳定性#

与通过货币资助的政府赤字和价格水平和通货膨胀税的拉弗曲线类似，我们现在已经具备了从不同的 $p_{- 1}, π_{- 1}^{*}$ 设置开始计算时间序列的能力。

现在我们将研究当初始条件 $p_{- 1}, π_{- 1}^{*}$ 偏离稳态值 $π_{u}$ 或 $π_{l}$ 时，系统的动态演化过程。

为了生成不同的初始条件，我们将:

选择一系列不同于稳态值的初始预期通胀率 $π_{- 1}^{*}$
根据货币需求方程，计算对应的初始价格水平 $p_{- 1} = m_{0} + α π_{- 1}^{*}$

让我们模拟通过改变初始 $π_{- 1}$ 和对应的 $p_{- 1}$ 生成的结果

πs = np.linspace(π_l, π_u, 10)

line_params = {'lw': 1.5,
               'marker': 'o',
               'markersize': 3}
              
π_bars = (π_l, π_u)
draw_iterations(πs, model, line_params, π_bars, num_steps=80)

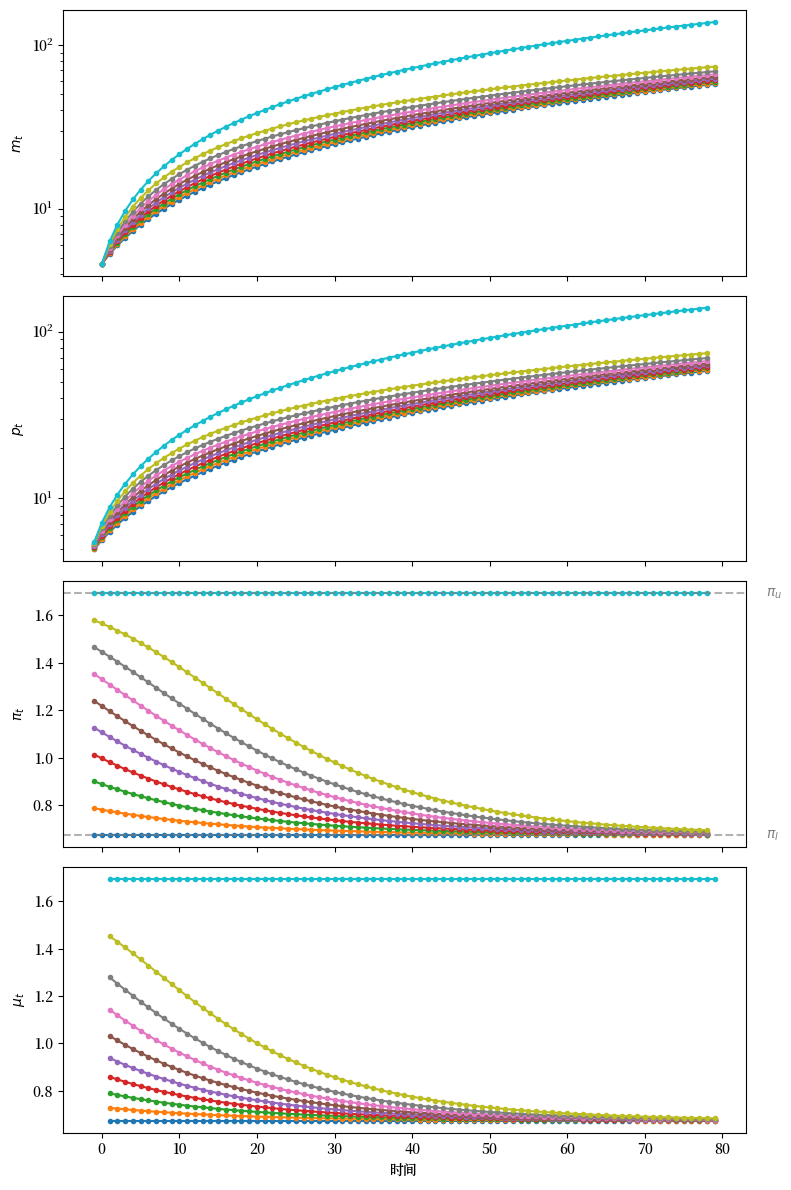
_images/e5410dc11828131fced66d64437f653fdc8fea67ff96038c6acddbe2267fc225.png — Fig. 31.2 从不同的 $π_{0}$ 初始值开始， $m_{t}$ 的路径（顶部图， $m$ 的对数标度）， $p_{t}$ （第二副图， $p$ 的对数标度）， $π_{t}$ （第三副图），和 $μ_{t}$ （底部图）#