18. 分布和概率#
18.1. 概述#
在本讲中，我们将使用 Python 快速介绍数据和概率分布。
!pip install --upgrade yfinance
import matplotlib.pyplot as plt
import matplotlib as mpl
import pandas as pd
import numpy as np
import yfinance as yf
import scipy.stats
import seaborn as sns
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']
18.2. 常见分布#
在本节中，我们将介绍几种常见概率分布的基本定义，并展示如何利用 SciPy 库来处理和分析这些分布。
18.2.1. 离散分布#
我们从离散分布开始。
离散分布由一组数值 \(S = \{x_1, \ldots, x_n\}\) 定义，并在 \(S\) 上有一个概率质量函数（PMF），它是一个从 \(S\) 到 \([0,1]\) 的函数 \(p\)，具有属性
我们说一个随机变量 \(X\) 服从分布 \(p\)，如果 \(X\) 取值为 \(x_i\) 的概率是 \(p(x_i)\)。
即，
具有分布 \(p\) 的随机变量 \(X\) 的均值或期望值是
期望值也被称为分布的一阶矩，是描述分布中心位置的重要统计量。
我们也将这个数字称为分布（由 \(p\) 表示）的均值。
\(X\) 的方差定义为
方差也称为分布的二阶中心矩。
\(X\) 的累积分布函数（CDF）定义为
这里 \(\mathbb 1\{\text{判断语句} \} = 1\) 如果 “判断语句” 为真，否则为零。
因此第二项取所有 \(x_i \leq x\) 并求它们概率的和。
18.2.1.1. 均匀分布#
一个简单的例子是均匀分布，它为每个可能的结果分配相同的概率，即 \(p(x_i) = 1/n\) 对于所有 \(i = 1, 2, \ldots, n\)。
在 Python 中，我们可以使用 SciPy 库来处理 \(S = \{1, \ldots, n\}\) 上的均匀分布：
n = 10
u = scipy.stats.randint(1, n+1)
计算均值和方差：
u.mean(), u.var()
(5.5, 8.25)
均值的公式是 \((n+1)/2\)，方差的公式是 \((n^2 - 1)/12\)。
现在让我们评估 PMF：
u.pmf(1)
0.1
u.pmf(2)
0.1
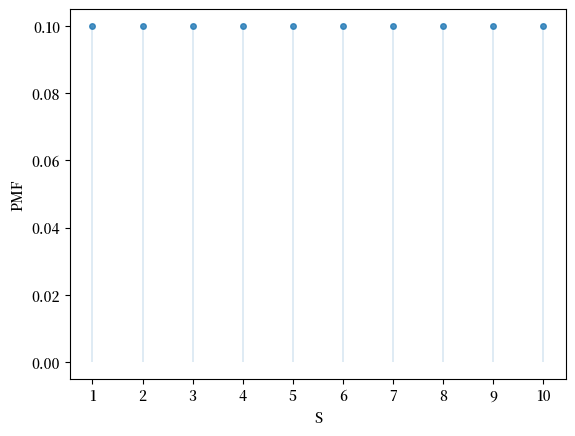
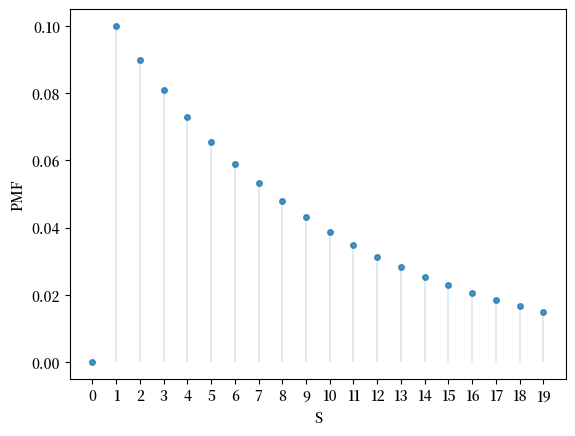
以下是 PMF 的图：
fig, ax = plt.subplots()
S = np.arange(1, n+1)
ax.plot(S, u.pmf(S), linestyle='', marker='o', alpha=0.8, ms=4)
ax.vlines(S, 0, u.pmf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('PMF')
plt.show()
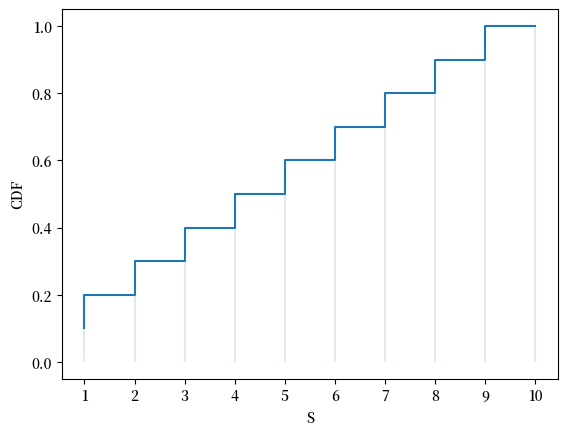
这里是 CDF 的图：
fig, ax = plt.subplots()
S = np.arange(1, n+1)
ax.step(S, u.cdf(S))
ax.vlines(S, 0, u.cdf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('CDF')
plt.show()
CDF 在\(x_i\)处跳升\(p(x_i)\)。
Exercise 18.1
使用均值公式 \((n+1)/2\) 和方差公式 \((n^2 - 1)/12\) 手动计算当 \(n=10\) 时的均值和方差。
将你计算的结果与 Python 函数 u.mean() 和 u.var() 返回的值进行比较，确认它们是否一致。
18.2.1.2. 伯努利分布#
另一个有用的分布是 \(S = \{0,1\}\) 上的伯努利分布，其 PMF 是：
这里 \(\theta \in [0,1]\) 是一个参数。
我们可以将这个分布视为对一个只有两种可能结果的随机试验进行概率建模，其成功概率是 \(\theta\)。
\(p(1) = \theta\) 表示试验成功（取值1）的概率是 \(\theta\)
\(p(0) = 1 - \theta\) 表示试验失败（取值0）的概率是 \(1-\theta\)
均值的公式是 \(\theta\)，方差的公式是 \(\theta(1-\theta)\)。
我们可以这样从 SciPy 导入 \(S = \{0,1\}\) 上的伯努利分布：
θ = 0.4
u = scipy.stats.bernoulli(θ)
这是 \(\theta=0.4\) 时的均值和方差：
u.mean(), u.var()
(0.4, 0.24)
我们可以评估 PMF 如下：
u.pmf(0), u.pmf(1)
(0.6, 0.4)
18.2.1.3. 二项分布#
另一个有用（而且更有趣）的分布是 \(S=\{0, \ldots, n\}\) 上的二项分布，其 PMF 为：
这里，\(\theta \in [0,1]\) 仍然是表示成功概率的参数。
二项分布描述了在\(n\)次独立的伯努利试验中，恰好获得\(i\)次成功的概率，其中每次试验成功的概率都是\(\theta\)。
一个直观的例子是：当\(\theta=0.5\)时，\(p(i)\)表示在\(n\)次公平硬币投掷中，恰好出现\(i\)次正面的概率。
二项分布的均值为\(n\theta\)，方差为\(n\theta(1-\theta)\)。
让我们通过一个具体例子来说明这个分布
n = 10
θ = 0.5
u = scipy.stats.binom(n, θ)
根据我们的公式，均值和方差是
n * θ, n * θ * (1 - θ)
(5.0, 2.5)
让我们看看SciPy是否给出了相同的结果：
u.mean(), u.var()
(5.0, 2.5)
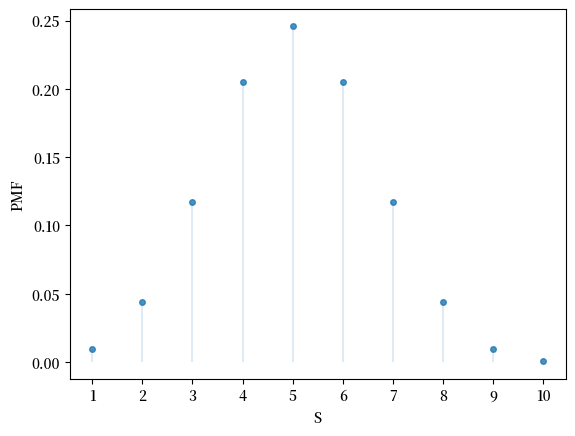
这是 PMF：
u.pmf(1)
0.009765625000000002
fig, ax = plt.subplots()
S = np.arange(1, n+1)
ax.plot(S, u.pmf(S), linestyle='', marker='o', alpha=0.8, ms=4)
ax.vlines(S, 0, u.pmf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('PMF')
plt.show()
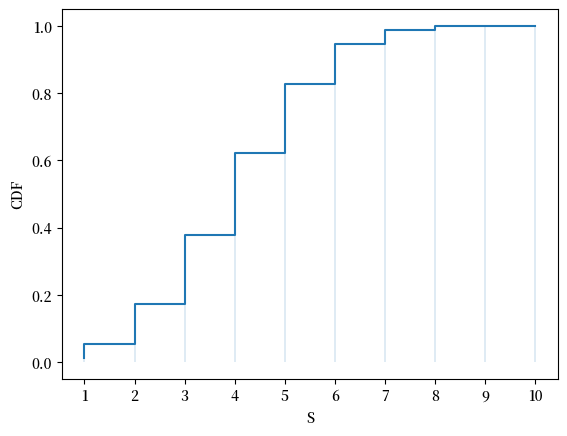
这是 CDF：
fig, ax = plt.subplots()
S = np.arange(1, n+1)
ax.step(S, u.cdf(S))
ax.vlines(S, 0, u.cdf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('CDF')
plt.show()
Exercise 18.2
使用u.pmf，验证我们上面给出的CDF定义是否计算出与u.cdf相同的函数。
Solution to Exercise 18.2
答案：
fig, ax = plt.subplots()
S = np.arange(1, n+1)
u_sum = np.cumsum(u.pmf(S))
ax.step(S, u_sum)
ax.vlines(S, 0, u_sum, lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('CDF')
plt.show()
我们可以看到输出图与上面的相同。
18.2.1.4. 几何分布#
几何分布是一种具有无限支持集 \(S = \{0, 1, 2, \ldots\}\) 的离散概率分布，其概率质量函数（PMF）为
其中参数 \(\theta \in [0,1]\) 表示成功的概率。
（当一个离散分布在无限多个点上赋予正概率时，我们称它具有无限支持。）
几何分布通常用来描述在一系列独立的伯努利试验中，首次成功出现前所需的失败次数。每次试验成功的概率都是 \(\theta\)。
因此，\(p(i)\) 表示在第一次成功之前恰好发生 \(i\) 次失败的概率。
这个分布的期望值（平均值）是 \((1-\theta)/\theta\)，方差是 \((1-\theta)/\theta^2\)。
让我们通过一个例子来说明：
θ = 0.1
u = scipy.stats.geom(θ)
u.mean(), u.var()
(10.0, 90.0)
这里是部分PMF：
fig, ax = plt.subplots()
n = 20
S = np.arange(n)
ax.plot(S, u.pmf(S), linestyle='', marker='o', alpha=0.8, ms=4)
ax.vlines(S, 0, u.pmf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('PMF')
plt.show()
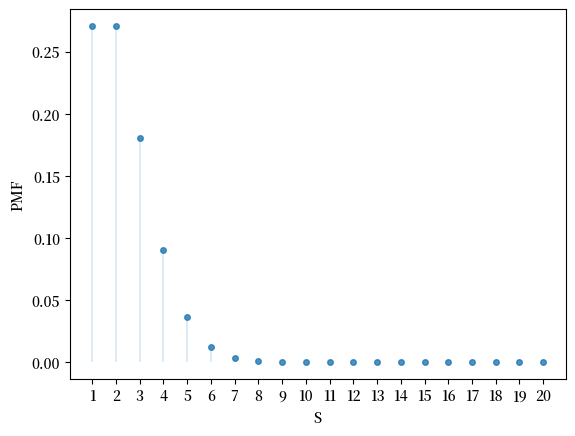
18.2.1.5. 泊松分布#
泊松分布是一种常见的离散概率分布，定义在非负整数集 \(S = \{0, 1, 2, \ldots\}\) 上。它由一个参数 \(\lambda > 0\) 控制，其概率质量函数（PMF）为：
泊松分布通常用于模拟在固定时间或空间内随机事件的发生次数。具体来说，\(p(i)\) 表示在给定区间内事件恰好发生 \(i\) 次的概率，其中事件以平均率 \(\lambda\) 独立随机发生。
这个分布的一个有趣特性是其均值和方差都等于参数 \(\lambda\)。
下面我们通过一个具体例子来展示泊松分布：
λ = 2
u = scipy.stats.poisson(λ)
u.mean(), u.var()
(2.0, 2.0)
这是概率质量函数：
u.pmf(1)
0.2706705664732254
fig, ax = plt.subplots()
S = np.arange(1, n+1)
ax.plot(S, u.pmf(S), linestyle='', marker='o', alpha=0.8, ms=4)
ax.vlines(S, 0, u.pmf(S), lw=0.2)
ax.set_xticks(S)
ax.set_xlabel('S')
ax.set_ylabel('PMF')
plt.show()
18.2.2. 连续分布#
连续分布通过概率密度函数（PDF）来描述，这是一个定义在实数集 \(\mathbb R\) 上的非负函数 \(p\)，满足
当随机变量 \(X\) 服从概率密度函数 \(p\) 时，任意区间 \([a, b]\) 上的概率可以通过积分计算：
与离散分布类似，连续随机变量的均值和方差也可以通过其概率密度函数计算，只需将求和替换为积分。
例如，随机变量 \(X\) 的均值计算为
\(X\) 的累积分布函数（CDF）定义为
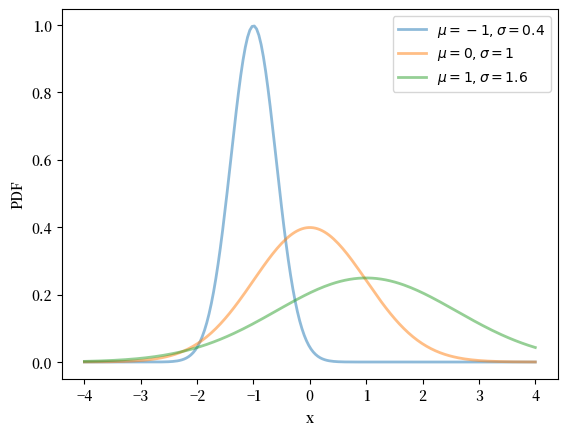
18.2.2.1. 正态分布#
正态分布是统计学中最常见也最重要的分布之一，其概率密度函数为
正态分布由两个参数决定：\(\mu \in \mathbb R\)（均值参数）和 \(\sigma \in (0, \infty)\)（标准差参数）。
通过积分计算可以验证，当随机变量 \(X\) 服从正态分布时，\(\mathbb{E}[X] = \mu\)，\(\text{Var}(X) = \sigma^2\)。
我们可以通过 SciPy 来计算正态分布的矩、PDF 和 CDF：
μ, σ = 0.0, 1.0
u = scipy.stats.norm(μ, σ)
u.mean(), u.var()
(0.0, 1.0)
下面是密度的图像——著名的“钟形曲线”：
μ_vals = [-1, 0, 1]
σ_vals = [0.4, 1, 1.6]
fig, ax = plt.subplots()
x_grid = np.linspace(-4, 4, 200)
for μ, σ in zip(μ_vals, σ_vals):
u = scipy.stats.norm(μ, σ)
ax.plot(x_grid, u.pdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\mu={μ}, \sigma={σ}$')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
plt.legend()
plt.show()
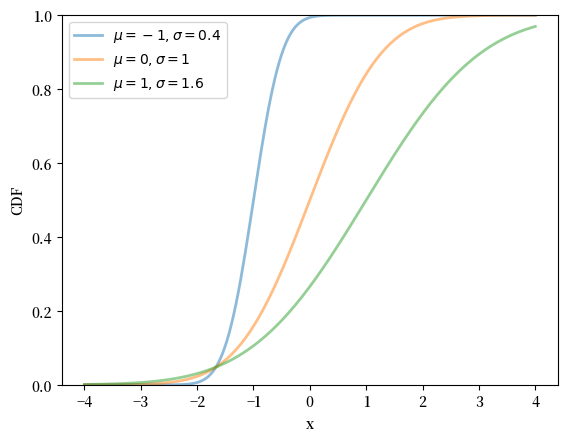
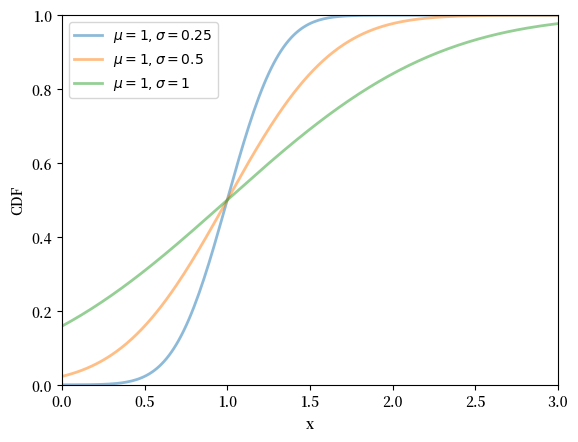
下面是 CDF 的图像：
fig, ax = plt.subplots()
for μ, σ in zip(μ_vals, σ_vals):
u = scipy.stats.norm(μ, σ)
ax.plot(x_grid, u.cdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\mu={μ}, \sigma={σ}$')
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('CDF')
plt.legend()
plt.show()
18.2.2.2. 对数正态分布#
对数正态分布是一个定义在正实数轴 \((0, \infty)\) 上的概率分布，其密度函数为
该分布由两个参数 \(\mu \in \mathbb{R}\) 和 \(\sigma > 0\) 决定。
对于服从对数正态分布的随机变量 \(X\)，其期望值为 \(\mathbb{E}[X] = \exp(\mu + \sigma^2/2)\)，方差为 \(\text{Var}(X) = [\exp(\sigma^2) - 1] \exp(2\mu + \sigma^2)\)。
对数正态分布与正态分布有着密切的关系：
如果随机变量 \(X\) 服从对数正态分布，那么 \(\log X\) 服从正态分布
反之，如果 \(Y\) 服从正态分布，那么 \(\exp(Y)\) 服从对数正态分布
我们可以使用 SciPy 来计算对数正态分布的矩、PDF 和 CDF：
μ, σ = 0.0, 1.0
u = scipy.stats.lognorm(s=σ, scale=np.exp(μ))
u.mean(), u.var()
(1.6487212707001282, 4.670774270471604)
μ_vals = [-1, 0, 1]
σ_vals = [0.25, 0.5, 1]
x_grid = np.linspace(0, 3, 200)
fig, ax = plt.subplots()
for μ, σ in zip(μ_vals, σ_vals):
u = scipy.stats.lognorm(σ, scale=np.exp(μ))
ax.plot(x_grid, u.pdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\mu={μ}, \sigma={σ}$')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
plt.legend()
plt.show()
fig, ax = plt.subplots()
μ = 1
for σ in σ_vals:
u = scipy.stats.norm(μ, σ)
ax.plot(x_grid, u.cdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\mu={μ}, \sigma={σ}$')
ax.set_ylim(0, 1)
ax.set_xlim(0, 3)
ax.set_xlabel('x')
ax.set_ylabel('CDF')
plt.legend()
plt.show()
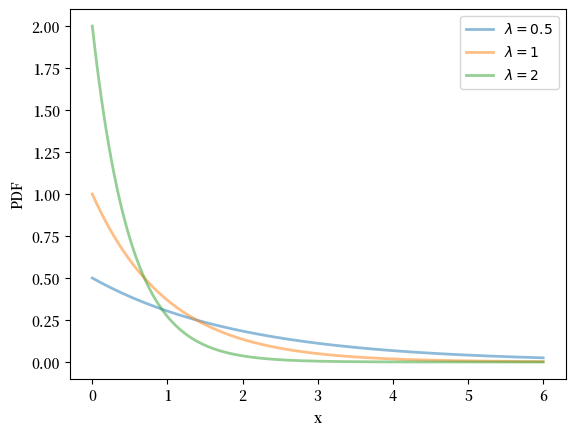
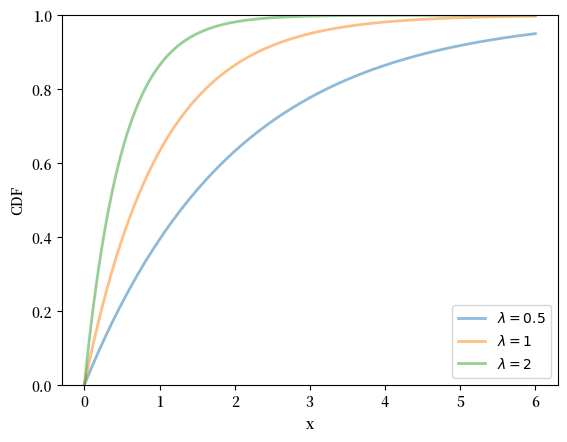
18.2.2.3. 指数分布#
指数分布是定义在 \(\left(0, \infty\right)\) 上的分布，其密度函数为
指数分布由参数 \(\lambda > 0\) 控制，它决定了分布的形状和尺度。
在许多方面，指数分布可以被看作是几何分布在连续情境下的自然推广。
对于指数分布，其均值为 \(1/\lambda\)，方差为 \(1/\lambda^2\)。这意味着 \(\lambda\) 越大，分布越集中在零附近。
下面我们使用SciPy来计算指数分布的统计特性并绘制其PDF和CDF：
λ = 1.0
u = scipy.stats.expon(scale=1/λ)
u.mean(), u.var()
(1.0, 1.0)
fig, ax = plt.subplots()
λ_vals = [0.5, 1, 2]
x_grid = np.linspace(0, 6, 200)
for λ in λ_vals:
u = scipy.stats.expon(scale=1/λ)
ax.plot(x_grid, u.pdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\lambda={λ}$')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
plt.legend()
plt.show()
fig, ax = plt.subplots()
for λ in λ_vals:
u = scipy.stats.expon(scale=1/λ)
ax.plot(x_grid, u.cdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\lambda={λ}$')
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('CDF')
plt.legend()
plt.show()
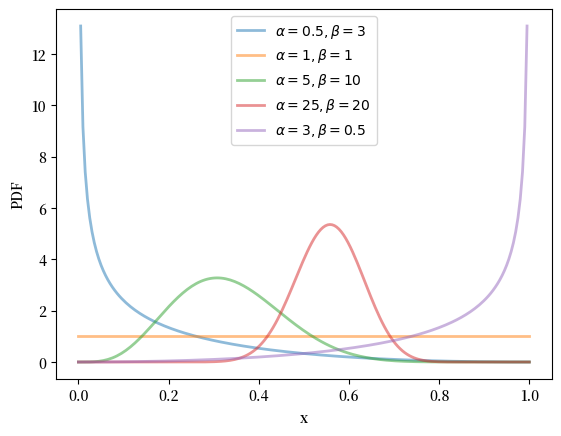
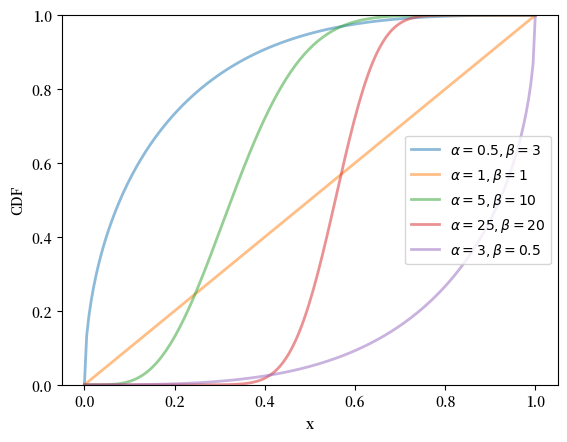
18.2.2.4. 贝塔分布#
贝塔分布是定义在 \((0, 1)\) 上的分布，其密度为
其中 \(\Gamma\) 是伽马函数。
(伽马函数的作用是使密度标准化，从而使其积分为一。)
此分布有两个参数，\(\alpha > 0\) 和 \(\beta > 0\)。
可以证明对于该分布，均值为 \(\alpha / (\alpha + \beta)\)，方差为 \(\alpha \beta / (\alpha + \beta)^2 (\alpha + \beta + 1)\)。
我们可以如下获得贝塔密度的矩、PDF 和 CDF：
α, β = 3.0, 1.0
u = scipy.stats.beta(α, β)
u.mean(), u.var()
(0.75, 0.0375)
α_vals = [0.5, 1, 5, 25, 3]
β_vals = [3, 1, 10, 20, 0.5]
x_grid = np.linspace(0, 1, 200)
fig, ax = plt.subplots()
for α, β in zip(α_vals, β_vals):
u = scipy.stats.beta(α, β)
ax.plot(x_grid, u.pdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\alpha={α}, \beta={β}$')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
plt.legend()
plt.show()
fig, ax = plt.subplots()
for α, β in zip(α_vals, β_vals):
u = scipy.stats.beta(α, β)
ax.plot(x_grid, u.cdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\alpha={α}, \beta={β}$')
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('CDF')
plt.legend()
plt.show()
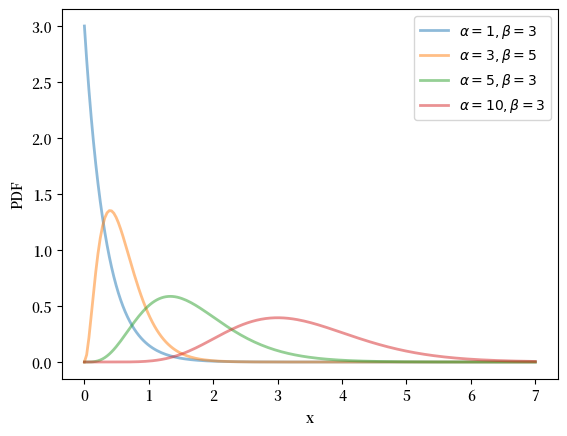
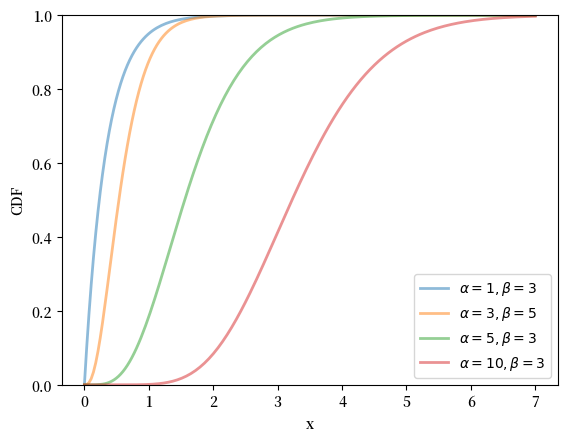
18.2.2.5. 伽马分布#
伽马分布是一种在正实数轴 \((0, \infty)\) 上的连续概率分布，其概率密度函数为
其中 \(\alpha > 0\) 是形状参数，\(\beta > 0\) 是速率参数，\(\Gamma(\alpha)\) 是伽马函数。
伽马分布的均值为 \(\alpha / \beta\)，方差为 \(\alpha / \beta^2\)。
伽马分布有一个直观的解释：当 \(\alpha\) 是正整数时，伽马分布随机变量可以看作是 \(\alpha\) 个独立的、均值为 \(1/\beta\) 的指数分布随机变量之和。这使得伽马分布在等待时间和可靠性分析中特别有用。
下面我们来计算伽马分布的矩、PDF 和 CDF：
α, β = 3.0, 2.0
u = scipy.stats.gamma(α, scale=1/β)
u.mean(), u.var()
(1.5, 0.75)
α_vals = [1, 3, 5, 10]
β_vals = [3, 5, 3, 3]
x_grid = np.linspace(0, 7, 200)
fig, ax = plt.subplots()
for α, β in zip(α_vals, β_vals):
u = scipy.stats.gamma(α, scale=1/β)
ax.plot(x_grid, u.pdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\alpha={α}, \beta={β}$')
ax.set_xlabel('x')
ax.set_ylabel('PDF')
plt.legend()
plt.show()
fig, ax = plt.subplots()
for α, β in zip(α_vals, β_vals):
u = scipy.stats.gamma(α, scale=1/β)
ax.plot(x_grid, u.cdf(x_grid),
alpha=0.5, lw=2,
label=fr'$\alpha={α}, \beta={β}$')
ax.set_ylim(0, 1)
ax.set_xlabel('x')
ax.set_ylabel('CDF')
plt.legend()
plt.show()
18.3. 观察到的分布#
有时候我们将观测到的数据或测量值称为“分布”。
例如，假设我们观察了10个人一年的收入：
data = [['Hiroshi', 1200],
['Ako', 1210],
['Emi', 1400],
['Daiki', 990],
['Chiyo', 1530],
['Taka', 1210],
['Katsuhiko', 1240],
['Daisuke', 1124],
['Yoshi', 1330],
['Rie', 1340]]
df = pd.DataFrame(data, columns=['name', 'income'])
df
| name | income | |
|---|---|---|
| 0 | Hiroshi | 1200 |
| 1 | Ako | 1210 |
| 2 | Emi | 1400 |
| 3 | Daiki | 990 |
| 4 | Chiyo | 1530 |
| 5 | Taka | 1210 |
| 6 | Katsuhiko | 1240 |
| 7 | Daisuke | 1124 |
| 8 | Yoshi | 1330 |
| 9 | Rie | 1340 |
在这种情况下，我们通常将这组收入数据称为”收入分布”。
这个术语可能有点让人困惑，因为严格来说，这只是一组数值，而不是真正的概率分布。
不过，正如我们接下来会看到的，这种观察到的数据分布（比如我们这里的收入数据）与理论上的概率分布有着密切的联系。
下面让我们来探索一些观察到的数据分布的特性。
18.3.1. 描述性统计#
当我们分析一组数据 \(\{x_1, \ldots, x_n\}\) 时，通常会计算一些基本的统计量来描述其特征。
最常用的统计量之一是样本均值，它代表数据的平均水平：
另一个重要的统计量是样本方差，它衡量数据的离散程度：
对于上面给出的收入分布，我们可以通过下面的方式计算这些数字：
x = df['income']
x.mean(), x.var()
(1257.4, 22680.933333333334)
Exercise 18.3
如果你尝试检查上述给出的样本均值和样本方差的公式是否能产生相同的数字，你会发现方差并不完全正确。这是因为SciPy使用的是 \(1/(n-1)\) 而不是 \(1/n\) 作为方差的前面的系数。（有些书籍就是这样定义样本方差的。）
用纸笔确认这一点。
18.3.2. 可视化#
让我们来看看我们可以用哪些方式来可视化一个或多个观察到的分布。
我们将讲解
直方图
核密度估计
小提琴图
18.3.2.1. 直方图#
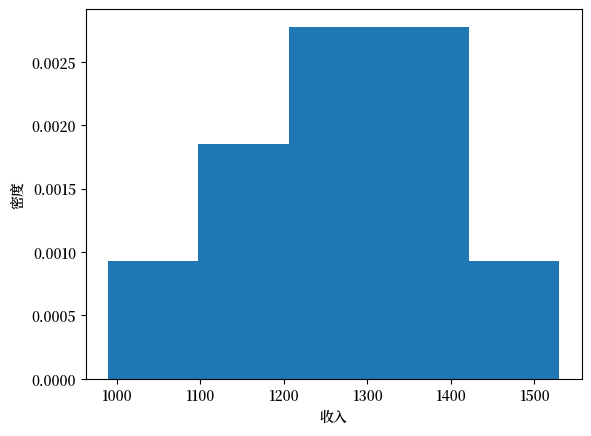
下面我们来绘制刚才创建的收入分布直方图：
fig, ax = plt.subplots()
ax.hist(x, bins=5, density=True, histtype='bar')
ax.set_xlabel('收入')
ax.set_ylabel('密度')
plt.show()
现在让我们来分析一个真实世界的数据分布案例。
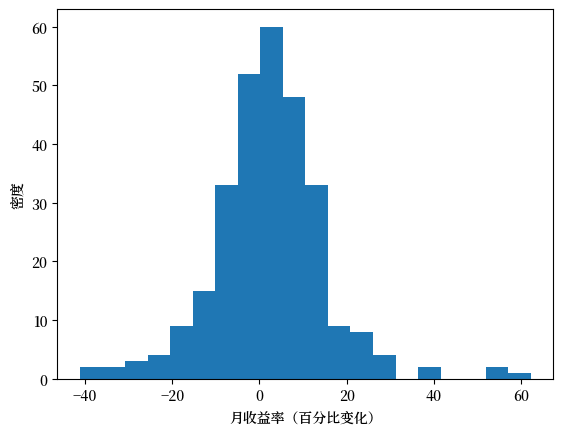
我们将研究亚马逊股票在2000年1月1日至2024年1月1日期间的月度收益率数据。
月度收益率表示股票价格每月的百分比变化，这是金融分析中的一个常用指标。
这样，我们就能获得一个包含24年间每月观测值的时间序列数据集。
df = yf.download('AMZN', '2000-1-1', '2024-1-1',
interval='1mo', auto_adjust=False)
prices = df['Adj Close']
x_amazon = prices.pct_change()[1:] * 100
x_amazon.head()
第一个观察结果是2000年1月的月回报（百分比变化），即
x_amazon.iloc[0]
Ticker
AMZN 6.679568
Name: 2000-02-01 00:00:00, dtype: float64
让我们将回报观测值转换成数组并制作直方图。
fig, ax = plt.subplots()
ax.hist(x_amazon, bins=20)
ax.set_xlabel('月收益率（百分比变化）')
ax.set_ylabel('密度')
plt.show()
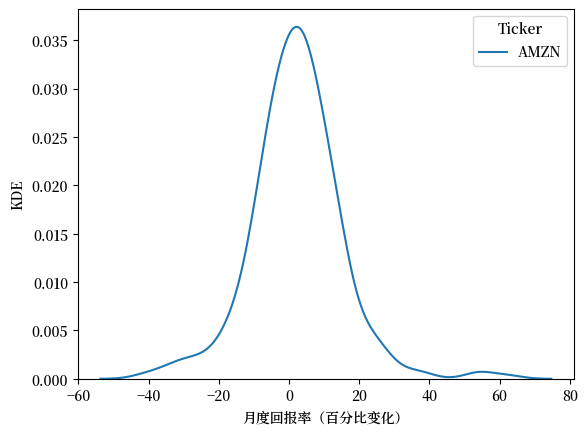
18.3.2.2. 核密度估计#
核密度估计（KDE）是一种更平滑地展示数据分布的方法，可以看作是直方图的进阶版本。
相比直方图的阶梯状外观，KDE生成连续的密度曲线，能更自然地反映数据的分布特征。
下面让我们用KDE来可视化亚马逊股票的月度收益率数据。
fig, ax = plt.subplots()
sns.kdeplot(x_amazon, ax=ax)
ax.set_xlabel('月度回报率（百分比变化）')
ax.set_ylabel('KDE')
plt.show()
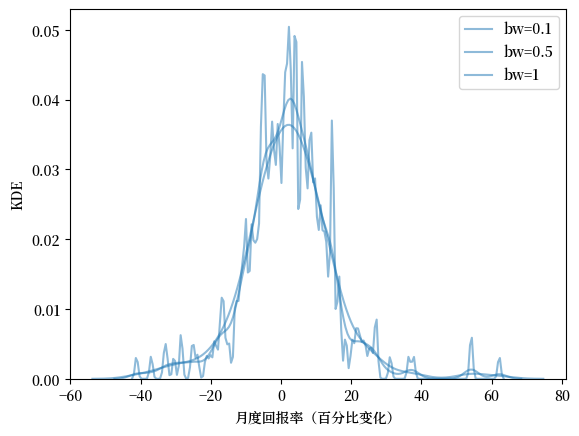
KDE的平滑程度取决于我们选择带宽的方式。
fig, ax = plt.subplots()
sns.kdeplot(x_amazon, ax=ax, bw_adjust=0.1, alpha=0.5, label="bw=0.1")
sns.kdeplot(x_amazon, ax=ax, bw_adjust=0.5, alpha=0.5, label="bw=0.5")
sns.kdeplot(x_amazon, ax=ax, bw_adjust=1, alpha=0.5, label="bw=1")
ax.set_xlabel('月度回报率（百分比变化）')
ax.set_ylabel('KDE')
plt.legend()
plt.show()
当我们使用较大的带宽时，KDE更加平滑。
一个合适的带宽既不应过于平滑（欠拟合），也不应过于曲折（过拟合）。
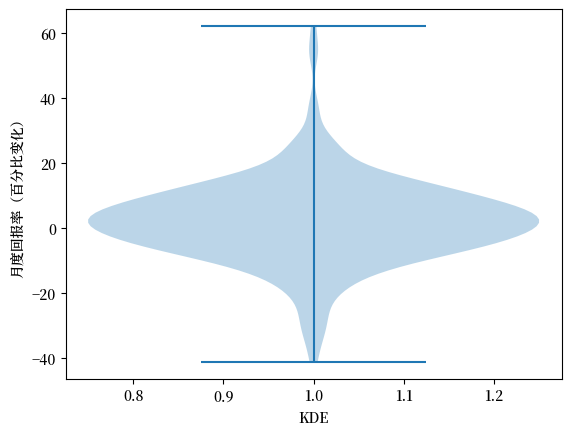
18.3.2.3. 小提琴图#
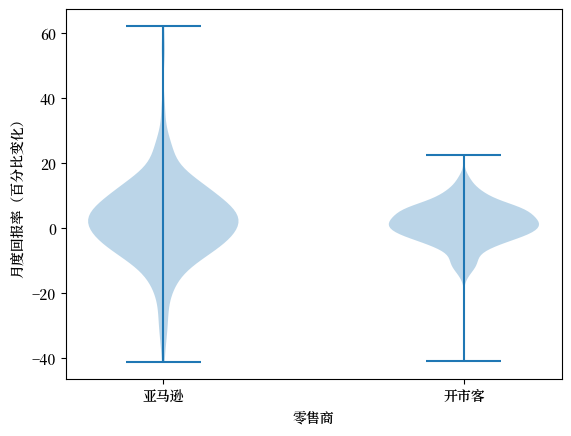
通过小提琴图展示观察到的分布是另一种方式。
fig, ax = plt.subplots()
ax.violinplot(x_amazon)
ax.set_ylabel('月度回报率（百分比变化）')
ax.set_xlabel('KDE')
plt.show()
小提琴图在比较多个数据集的分布特征时特别有用，它能直观地展示数据的密度和范围。
接下来，让我们用小提琴图来对比亚马逊和开市客这两家零售巨头的月度股票回报率分布情况。
df = yf.download('COST', '2000-1-1', '2024-1-1',
interval='1mo', auto_adjust=False)
prices = df['Adj Close']
x_costco = prices.pct_change()[1:] * 100
fig, ax = plt.subplots()
ax.violinplot([x_amazon['AMZN'], x_costco['COST']])
ax.set_ylabel('月度回报率（百分比变化）')
ax.set_xlabel('零售商')
ax.set_xticks([1, 2])
ax.set_xticklabels(['亚马逊', '开市客'])
plt.show()
18.3.3. 与概率分布的联系#
现在让我们探讨观察数据分布与理论概率分布之间的关系。
在数据分析中，我们常常会假设观察到的数据来自某个特定的概率分布，这有助于我们理解和建模数据的行为。
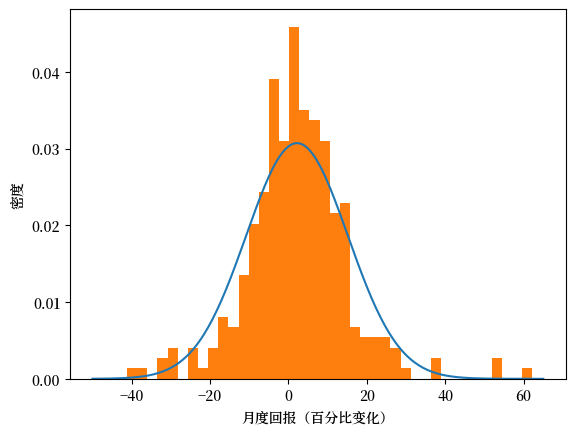
以亚马逊的股票回报为例，我们可以尝试用正态分布来拟合这些数据。
（虽然股票回报通常不完全符合正态分布，但这种简化假设在初步分析中很有价值。）
下面，我们将用亚马逊回报数据的样本均值和样本方差来构建一个匹配的正态分布，然后通过可视化比较理论分布与实际数据的吻合度。
μ = x_amazon.mean()
σ_squared = x_amazon.var()
σ = np.sqrt(σ_squared)
u = scipy.stats.norm(μ, σ)
x_grid = np.linspace(-50, 65, 200)
fig, ax = plt.subplots()
ax.plot(x_grid, u.pdf(x_grid))
ax.hist(x_amazon, density=True, bins=40)
ax.set_xlabel('月度回报（百分比变化）')
ax.set_ylabel('密度')
plt.show()
可以看出，直方图与理论密度曲线的匹配度并不理想。
这主要是因为亚马逊的股票回报数据并不完全符合正态分布 — 我们将在重尾分布章节中详细探讨这个现象。
如果数据确实来自正态分布，拟合效果会好得多。
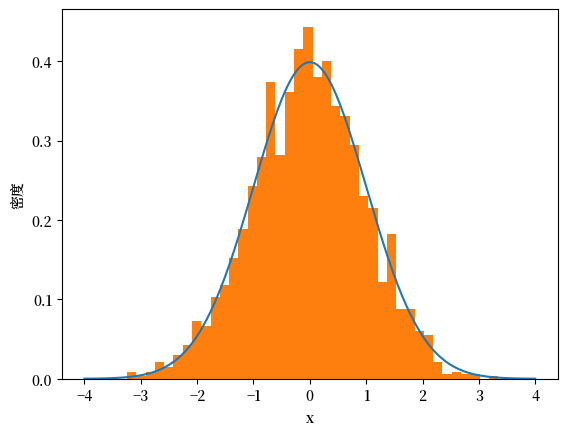
为了验证这一点，我们可以做一个简单的实验：
从标准正态分布中生成随机样本
绘制这些样本的直方图，并与理论密度曲线进行比较
μ, σ = 0, 1
u = scipy.stats.norm(μ, σ)
N = 2000
x_draws = u.rvs(N)
x_grid = np.linspace(-4, 4, 200)
fig, ax = plt.subplots()
ax.plot(x_grid, u.pdf(x_grid))
ax.hist(x_draws, density=True, bins=40)
ax.set_xlabel('x')
ax.set_ylabel('密度')
plt.show()
值得注意的是，随着观测数量 \(N\) 的增加，直方图与理论密度曲线的拟合效果会逐渐改善。
这种现象体现了”大数定律”的原理，我们将在后续章节中深入探讨。