44. 简单线性回归模型#

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

以下的简单回归模型估计了两个变量 $x_{i}$ 和 $y_{i}$ 之间的关系

y_{i} = α + β x_{i} + ϵ_{i}, i = 1, 2, . . ., N

其中 $ϵ_{i}$ 表示最佳拟合线与给定 $x_{i}$ 的样本值 $y_{i}$ 之间的误差。

我们的目标是选择 $α$ 和 $β$ 的值来为一些适用于变量 $x_{i}$ 和 $y_{i}$ 的数据构建一条“最佳”拟合线。

让我们假设存在一个简单的数据集，其中包含 10 个变量 $x_{i}$ 和 $y_{i}$ 的观测值：

	$y_{i}$	$x_{i}$
1	2000	32
2	1000	21
3	1500	24
4	2500	35
5	500	10
6	900	11
7	1100	22
8	1500	21
9	1800	27
10	250	2

让我们把 $y_{i}$ 视为一个冰淇淋车的销售额，而 $x_{i}$ 是记录当天气温（摄氏度）的变量。

x = [32, 21, 24, 35, 10, 11, 22, 21, 27, 2]
y = [2000, 1000, 1500, 2500, 500, 900, 1100, 1500, 1800, 250]
df = pd.DataFrame([x,y]).T
df.columns = ['X', 'Y']
df

	X	Y
0	32	2000
1	21	1000
2	24	1500
3	35	2500
4	10	500
5	11	900
6	22	1100
7	21	1500
8	27	1800
9	2	250

我们可以通过散点图来观察 $y_{i}$ （冰淇淋销售额（美元($’s)）和 $x_{i}$ （摄氏度）之间的关系。

ax = df.plot(
    x='X', 
    y='Y', 
    kind='scatter', 
    ylabel=r'冰淇淋销售额（$\'s）', 
    xlabel='摄氏度'
)

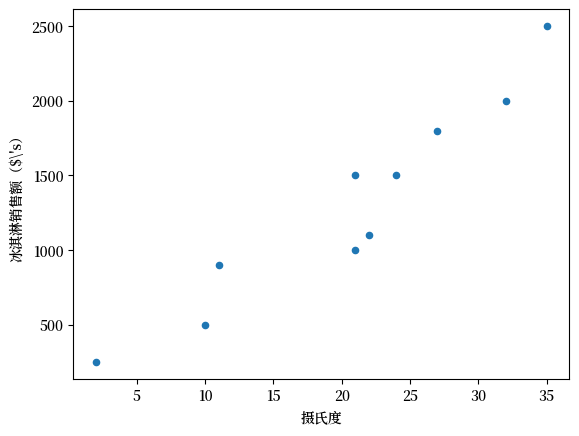
_images/279b29dd784e43cef54622443b93d406a594a19a450a92702518347d4bb27aec.png — Fig. 44.1 散点图#

如你所见，数据表明在较热的日子里通常会卖出较多的冰淇淋。

为了构建数据的线性模型，我们需要选择代表“最佳”拟合线的 $α$ 和 $β$ 值，使得

\hat{y_{i}} = \hat{α} + \hat{β} x_{i}

让我们从 $α = 5$ 和 $β = 10$ 开始

α = 5
β = 10
df['Y_hat'] = α + β * df['X']

fig, ax = plt.subplots()
ax = df.plot(x='X',y='Y', kind='scatter', ax=ax)
ax = df.plot(x='X',y='Y_hat', kind='line', ax=ax, label=r'$\hat Y$')
plt.show()

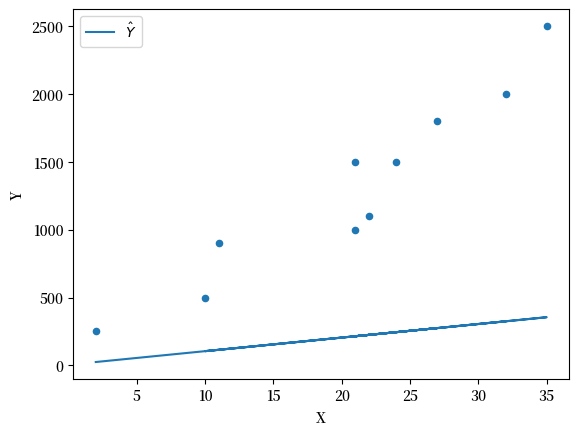
_images/468063cda355bbddd56f1b13ddc1a67f28c47f78cf8cc8dfb85b8029108263a7.png — Fig. 44.2 带有拟合线的散点图#

我们可以看到这个模型没法很好地估计两者的关系。

我们可以继续猜测，并通过调整参数迭代出一条 “最佳 ”拟合线。

β = 100
df['Y_hat'] = α + β * df['X']

fig, ax = plt.subplots()
ax = df.plot(x='X',y='Y', kind='scatter', ax=ax)
ax = df.plot(x='X',y='Y_hat', kind='line', ax=ax, label=r'$\hat Y$')
plt.show()

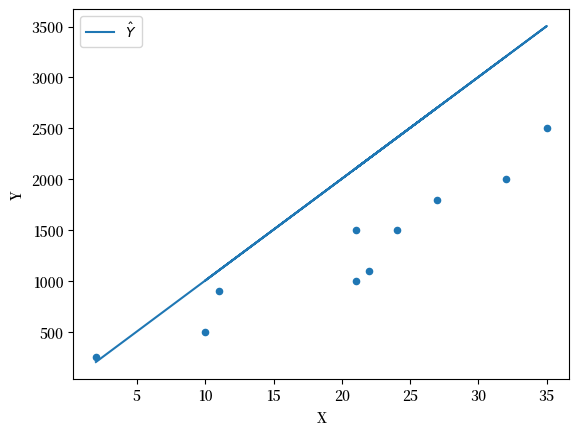
_images/24a9ea5ecff2e64e5e4b2990e38578a7a2b9ec6050f665a73b5673d0e8da99cf.png — Fig. 44.3 带拟合线的散点图 #2#

β = 65
df['Y_hat'] = α + β * df['X']

fig, ax = plt.subplots()
ax = df.plot(x='X',y='Y', kind='scatter', ax=ax)
yax = df.plot(x='X',y='Y_hat', kind='line', ax=ax, color='g', label=r'$\hat Y$')
plt.show()

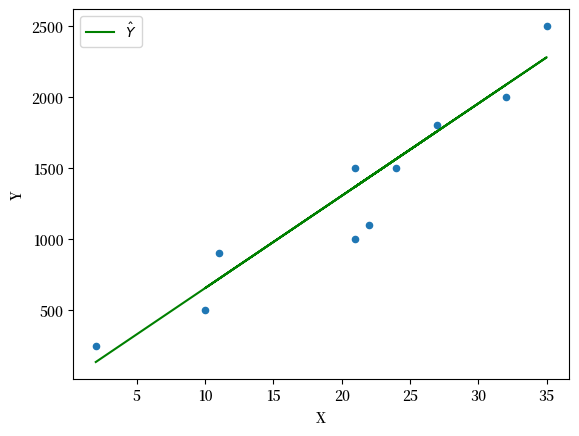
_images/f63b5c3ece86f59b82c8b04503b9cfdb737e92d07c925a576570bbcc7004eef1.png — Fig. 44.4 带拟合线的散点图 #3#

与其不断猜测参数值，我们可以把这个问题转化为一个优化问题，用数学方法来求解最优的参数。

为此，我们先来定义一个重要的概念：残差（residual）。残差 $ϵ_{i}$ 是实际观测值 $y_{i}$ 与模型预测值 ${\hat{y}}_{i}$ 之间的差异。

\begin{array}{r} \begin{aligned} {\hat{e}}_{i} & = y_{i} - {\hat{y}}_{i} \\ = y_{i} - \hat{α} - \hat{β} x_{i} \end{aligned} \end{array}

df['error'] = df['Y_hat'] - df['Y']

df

	X	Y	Y_hat	error
0	32	2000	2085	85
1	21	1000	1370	370
2	24	1500	1565	65
3	35	2500	2280	-220
4	10	500	655	155
5	11	900	720	-180
6	22	1100	1435	335
7	21	1500	1370	-130
8	27	1800	1760	-40
9	2	250	135	-115

fig, ax = plt.subplots()
ax = df.plot(x='X',y='Y', kind='scatter', ax=ax)
yax = df.plot(x='X',y='Y_hat', kind='line', ax=ax, color='g', label=r'$\hat Y$')
plt.vlines(df['X'], df['Y_hat'], df['Y'], color='r')
plt.show()

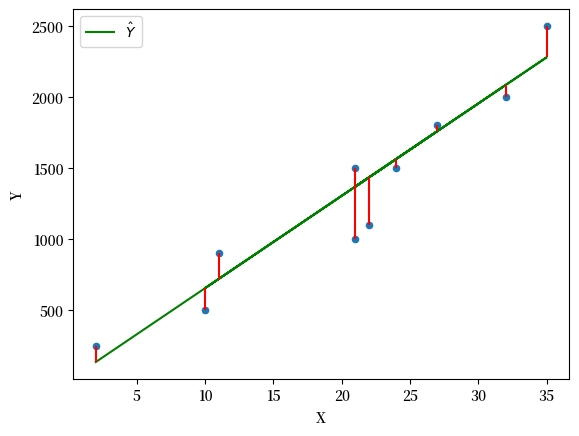
_images/9b40c1c9796b8cd275ca8bcee90a1dc046c31ef45605f0cd320d90a37b9122f0.png — Fig. 44.5 残差图#

普通最小二乘方法 (OLS) 通过 最小化 残差平方和 (SSR) 来选择 $α$ 和 $β$ 的值。

min_{α, β} \sum_{i = 1}^{N} {\hat{e}}_{i}^{2} = min_{α, β} \sum_{i = 1}^{N} (y_{i} - α - β x_{i})^{2}

我们称之为成本函数

C = \sum_{i = 1}^{N} (y_{i} - α - β x_{i})^{2}

我们希望通过调整参数 $α$ 和 $β$ 来最小化这个成本函数。

44.1. 残差相对于 $α$ 和 $β$ 是如何变化的#

首先，我们看看总残差相对于 $β$ 的变化（保持截距 $α$ 不变）

我们从下一节可以知道 $α$ 和 $β$ 的最优值是：

β_optimal = 64.38
α_optimal = -14.72

我们可以计算一系列 $β$ 值的残差

errors = {}
for β in np.arange(20,100,0.5):
    errors[β] = abs((α_optimal + β * df['X']) - df['Y']).sum()

绘制残差图

ax = pd.Series(errors).plot(xlabel='β', ylabel='残差')
plt.axvline(β_optimal, color='r');

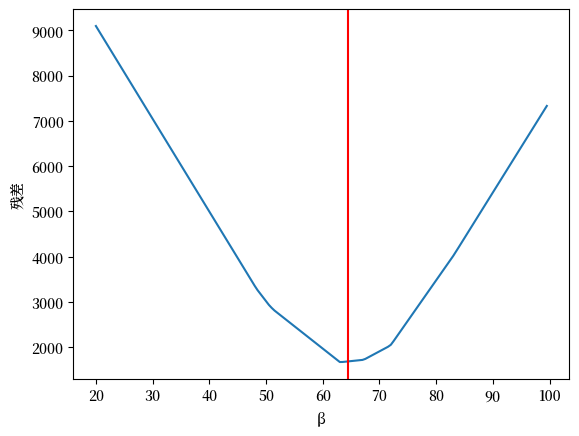
_images/233a641767a74e980b7239f1c74007309d7db6a2ef1ca9855e667efdeb374112.png — Fig. 44.6 绘制残差图#

现在我们改变 $α$ （保持 $β$ 不变）

errors = {}
for α in np.arange(-500,500,5):
    errors[α] = abs((α + β_optimal * df['X']) - df['Y']).sum()

绘制残差图

ax = pd.Series(errors).plot(xlabel='α', ylabel='残差')
plt.axvline(α_optimal, color='r');

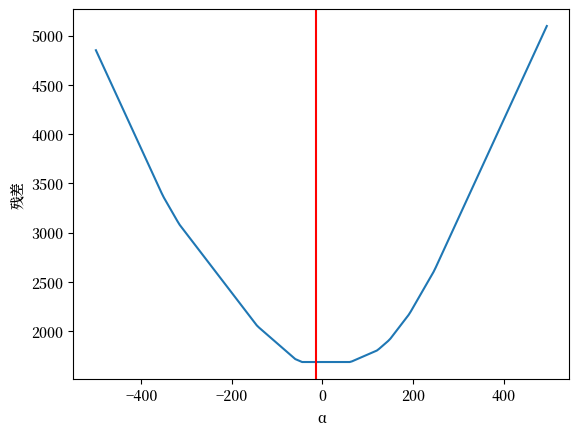
_images/edd915afb3bf4d63fe48fe30a95a3935a7df289c89b10f6a0d385c282d367870.png — Fig. 44.7 绘制残差图 (2)#

44.2. 计算最优值#

现在让我们使用微积分来解决优化问题，并计算出 $α$ 和 $β$ 的最优值，以找到普通最小二乘（OLS）解。

首先对 $α$ 取偏导

\frac{\partial C}{\partial α} [\sum_{i = 1}^{N} (y_{i} - α - β x_{i})^{2}]

并将其设为 $0$

0 = \sum_{i = 1}^{N} - 2 (y_{i} - α - β x_{i})

我们可以通过两边除以 $- 2$ 来移除求和中的常数 $- 2$

0 = \sum_{i = 1}^{N} (y_{i} - α - β x_{i})

现在我们可以将这个方程分解成几个组成部分

0 = \sum_{i = 1}^{N} y_{i} - \sum_{i = 1}^{N} α - β \sum_{i = 1}^{N} x_{i}

中间项是常数 $α$ 从 $i = 1, . . . N$ 进行直接相加得到的

0 = \sum_{i = 1}^{N} y_{i} - N * α - β \sum_{i = 1}^{N} x_{i}

重新排列各项可得

α = \frac{\sum_{i = 1}^{N} y_{i} - β \sum_{i = 1}^{N} x_{i}}{N}

我们可以发现分解成两个分数后，它们分别是均值 $\bar{y_{i}}$ 和 $\bar{x_{i}}$

(44.1)#

α = \bar{y_{i}} - β \bar{x_{i}}

回到成本函数 $C$ ，现在我们对 $β$ 取偏导

\frac{\partial C}{\partial β} [\sum_{i = 1}^{N} (y_{i} - α - β x_{i})^{2}]

并将其设为 $0$

0 = \sum_{i = 1}^{N} - 2 x_{i} (y_{i} - α - β x_{i})

我们可以通过将两边除以 $- 2$ ，再次将常数从求和中取出

0 = \sum_{i = 1}^{N} x_{i} (y_{i} - α - β x_{i})

进一步化简

0 = \sum_{i = 1}^{N} (x_{i} y_{i} - α x_{i} - β x_{i}^{2})

现在代入 $α$

0 = \sum_{i = 1}^{N} (x_{i} y_{i} - (\bar{y_{i}} - β \bar{x_{i}}) x_{i} - β x_{i}^{2})

重新排列各项

0 = \sum_{i = 1}^{N} (x_{i} y_{i} - \bar{y_{i}} x_{i} - β \bar{x_{i}} x_{i} - β x_{i}^{2})

这个方程可以被分成两个求和

0 = \sum_{i = 1}^{N} (x_{i} y_{i} - \bar{y_{i}} x_{i}) + β \sum_{i = 1}^{N} (\bar{x_{i}} x_{i} - x_{i}^{2})

得到 $β$ 的解

(44.2)#

β = \frac{\sum_{i = 1}^{N} (x_{i} y_{i} - \bar{y_{i}} x_{i})}{\sum_{i = 1}^{N} (x_{i}^{2} - \bar{x_{i}} x_{i})}

我们现在可以使用(44.1) 和 (44.2) 来计算 $α$ 和 $β$ 的最优值

计算 $β$

df = df[['X','Y']].copy()  # 原始数据

# 计算样本均值
x_bar = df['X'].mean()
y_bar = df['Y'].mean()

现在我们用10个观察值进行计算，然后把分子和分母分别求和

# 计算求和项
df['num'] = df['X'] * df['Y'] - y_bar * df['X']
df['den'] = pow(df['X'],2) - x_bar * df['X']
β = df['num'].sum() / df['den'].sum()
print(β)

64.37665782493369

计算 $α$

α = y_bar - β * x_bar
print(α)

-14.72148541114052

现在我们可以绘制OLS解

df['Y_hat'] = α + β * df['X']
df['error'] = df['Y_hat'] - df['Y']

fig, ax = plt.subplots()
ax = df.plot(x='X',y='Y', kind='scatter', ax=ax)
yax = df.plot(x='X',y='Y_hat', kind='line', ax=ax, color='g', label=r'$\hat Y$')
plt.vlines(df['X'], df['Y_hat'], df['Y'], color='r');

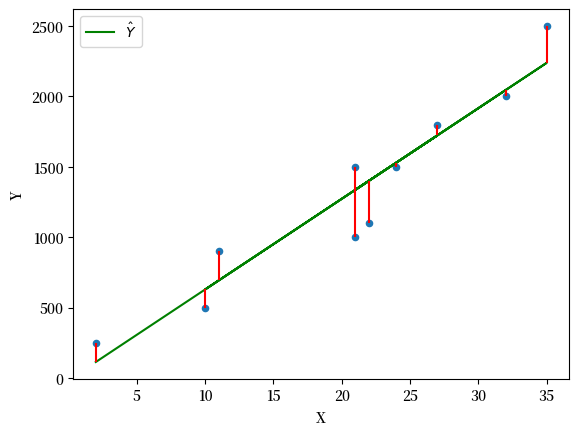
_images/b354f127d932a904b93d5c2bd44d6524ced7770ad67006ed938a340d65f0f721.png — Fig. 44.8 OLS最佳拟合线#

Exercise 44.1

现在你已经知道了使用OLS解决简单线性回归模型的方程，你可以开始运行自己的回归来构建 $y$ 和 $x$ 之间的模型了。

让我们考虑两个经济变量，人均GDP和预期寿命。

你认为它们之间的关系会是怎样的？
从our world in data中搜集一些数据
使用pandas导入csv格式的数据，并绘制几个不同国家的图表
使用(44.1) 和 (44.2)计算 $α$ 和 $β$ 的最优值
使用OLS绘制最佳拟合线
解释系数并用一句话总结人均GDP和预期寿命之间的关系

Solution to Exercise 44.1

第2问： 从our world in data中搜集一些数据

如果你遇到困难，可以从这里下载数据副本

第3问： 使用pandas导入csv格式的数据并绘制几个感兴趣的国家的图表

data_url = "https://github.com/QuantEcon/lecture-python-intro/raw/main/lectures/_static/lecture_specific/simple_linear_regression/life-expectancy-vs-gdp-per-capita.csv"
df = pd.read_csv(data_url, nrows=10)

df

	Entity	Code	Year	Life expectancy at birth (historical)	GDP per capita	417485-annotations	Population (historical estimates)	Continent
0	Abkhazia	OWID_ABK	2015	NaN	NaN	NaN	NaN	Asia
1	Afghanistan	AFG	1950	27.7	1156.0	NaN	7480464.0	NaN
2	Afghanistan	AFG	1951	28.0	1170.0	NaN	7571542.0	NaN
3	Afghanistan	AFG	1952	28.4	1189.0	NaN	7667534.0	NaN
4	Afghanistan	AFG	1953	28.9	1240.0	NaN	7764549.0	NaN
5	Afghanistan	AFG	1954	29.2	1245.0	NaN	7864289.0	NaN
6	Afghanistan	AFG	1955	29.9	1246.0	NaN	7971933.0	NaN
7	Afghanistan	AFG	1956	30.4	1278.0	NaN	8087730.0	NaN
8	Afghanistan	AFG	1957	30.9	1253.0	NaN	8210207.0	NaN
9	Afghanistan	AFG	1958	31.5	1298.0	NaN	8333827.0	NaN

从Our World in Data下载的数据包含了全球各国的人均GDP和预期寿命数据。

在导入完整数据集之前，我们先看看前几行数据来了解其结构。这样可以帮助我们确定哪些列是我们真正需要的。

我们可以看到数据集中包含了一些不必要的列，比如Continent。

让我们选择我们需要的列来创建一个更简洁的数据集：

cols = ['Code', 'Year', 'Life expectancy at birth (historical)', 'GDP per capita']
df = pd.read_csv(data_url, usecols=cols)
df

	Code	Year	Life expectancy at birth (historical)	GDP per capita
0	OWID_ABK	2015	NaN	NaN
1	AFG	1950	27.7	1156.0
2	AFG	1951	28.0	1170.0
3	AFG	1952	28.4	1189.0
4	AFG	1953	28.9	1240.0
...	...	...	...	...
62151	ZWE	1946	NaN	NaN
62152	ZWE	1947	NaN	NaN
62153	ZWE	1948	NaN	NaN
62154	ZWE	1949	NaN	NaN
62155	ALA	2015	NaN	NaN

62156 rows × 4 columns

有时候重命名列名可以让我们在DataFrame中更方便进行操作

df.columns = ["cntry", "year", "life_expectancy", "gdppc"]
df

	cntry	year	life_expectancy	gdppc
0	OWID_ABK	2015	NaN	NaN
1	AFG	1950	27.7	1156.0
2	AFG	1951	28.0	1170.0
3	AFG	1952	28.4	1189.0
4	AFG	1953	28.9	1240.0
...	...	...	...	...
62151	ZWE	1946	NaN	NaN
62152	ZWE	1947	NaN	NaN
62153	ZWE	1948	NaN	NaN
62154	ZWE	1949	NaN	NaN
62155	ALA	2015	NaN	NaN

62156 rows × 4 columns

我们可以看到存在NaN值，这表示缺失数据，所以让我们继续删除这些数据

df.dropna(inplace=True)

df

	cntry	year	life_expectancy	gdppc
1	AFG	1950	27.7	1156.0000
2	AFG	1951	28.0	1170.0000
3	AFG	1952	28.4	1189.0000
4	AFG	1953	28.9	1240.0000
5	AFG	1954	29.2	1245.0000
...	...	...	...	...
61960	ZWE	2014	58.8	1594.0000
61961	ZWE	2015	59.6	1560.0000
61962	ZWE	2016	60.3	1534.0000
61963	ZWE	2017	60.7	1582.3662
61964	ZWE	2018	61.4	1611.4052

12445 rows × 4 columns

通过删除缺失值，我们的数据集从62156行减少到了12445行。

现在我们有了一个清理过的数据集，包含了不同国家在不同年份的预期寿命和人均GDP数据。

在进行任何分析之前，我们应该先仔细了解数据的特点。一个重要的问题是: 不同国家在不同时期的数据是否完整?

让我们先来看看预期寿命数据的分布情况

le_years = df[['cntry', 'year', 'life_expectancy']].set_index(['cntry', 'year']).unstack()['life_expectancy']
le_years

year	1543	1548	1553	1558	1563	1568	1573	1578	1583	1588	...	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
cntry
AFG	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	60.4	60.9	61.4	61.9	62.4	62.5	62.7	63.1	63.0	63.1
AGO	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	55.8	56.7	57.6	58.6	59.3	60.0	60.7	61.1	61.7	62.1
ALB	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	77.8	77.9	78.1	78.1	78.1	78.4	78.6	78.9	79.0	79.2
ARE	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	78.0	78.3	78.5	78.7	78.9	79.0	79.2	79.3	79.5	79.6
ARG	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	75.9	75.7	76.1	76.5	76.5	76.8	76.8	76.3	76.8	77.0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
VNM	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	73.5	73.5	73.7	73.7	73.8	73.9	73.9	73.9	74.0	74.0
YEM	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	67.2	67.3	67.4	67.3	67.5	67.4	65.9	66.1	66.0	64.6
ZAF	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	57.4	58.9	60.7	61.8	62.5	63.4	63.9	64.7	65.4	65.7
ZMB	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	55.3	56.8	57.8	58.9	59.9	60.7	61.2	61.8	62.1	62.3
ZWE	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	48.1	50.7	53.3	55.6	57.5	58.8	59.6	60.3	60.7	61.4

166 rows × 310 columns

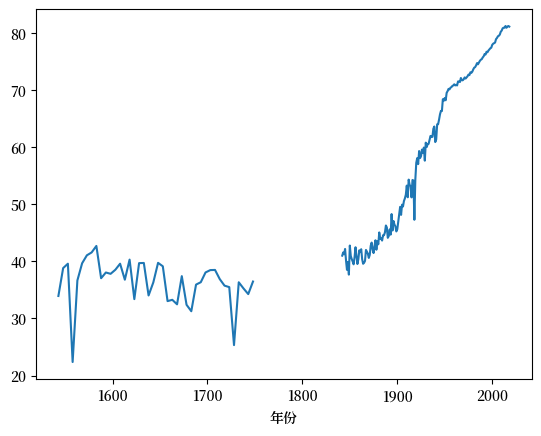
如你所见，有很多国家在1543年的数据是不可用的！

哪个国家报告了这些数据？

le_years[~le_years[1543].isna()]

year	1543	1548	1553	1558	1563	1568	1573	1578	1583	1588	...	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018
cntry
GBR	33.94	38.82	39.59	22.38	36.66	39.67	41.06	41.56	42.7	37.05	...	80.2	80.4	80.8	80.9	80.9	81.2	80.9	81.1	81.2	81.1

1 rows × 310 columns

你可以看到，只有大不列颠（GBR）的数据是可用的

你还可以更仔细地观察时间序列，发现即使对于GBR，它也是不连续的。

le_years.loc['GBR'].plot(xlabel="年份")

<Axes: xlabel='年份'>

_images/5579f352786dc625be43615dbe51327a29b810e7ecb2586708e8ca9802c6a319.png

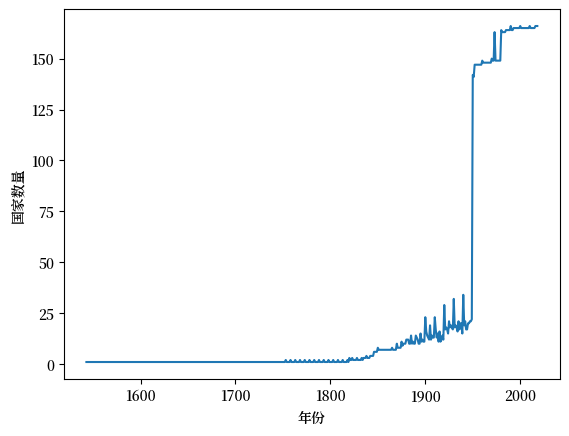
实际上我们可以使用pandas快速检查每个年份涵盖了多少个国家

le_years.stack().unstack(level=0).count(axis=1).plot(xlabel="年份", ylabel="国家数量");

_images/ad6a988ec96196da5e333b12c5d6e0d8e167b81e2947415ea6133abc75afad37.png

所以很明显，如果你进行横断面比较，那么最近的数据将包括更广泛的国家

现在让我们考虑数据集中最近的一年，也就是2018

df = df[df.year == 2018].reset_index(drop=True).copy()

df.plot(x='gdppc', y='life_expectancy', kind='scatter', xlabel="人均GDP", ylabel="预期寿命（年）",);

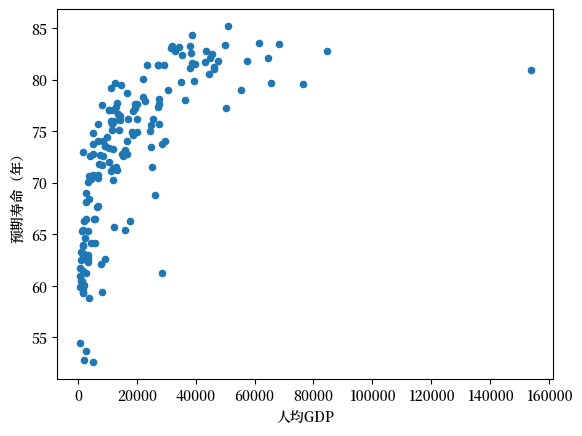
_images/eae193ff5d2b4ed74d2de5a484ee871d0b7598be61e8f4da6c5c19d987dff7be.png

这些数据显示了一些有趣的关系。

许多国家的人均GDP相近，但预期寿命差别很大
人均GDP与预期寿命之间似乎存在正向关系。人均GDP较高的国家往往拥有更高的预期寿命

虽然普通最小二乘法（OLS）主要用于线性关系，但我们可以通过对变量进行适当的转换（比如取对数），使非线性关系转化为线性关系，从而仍然可以使用OLS方法。

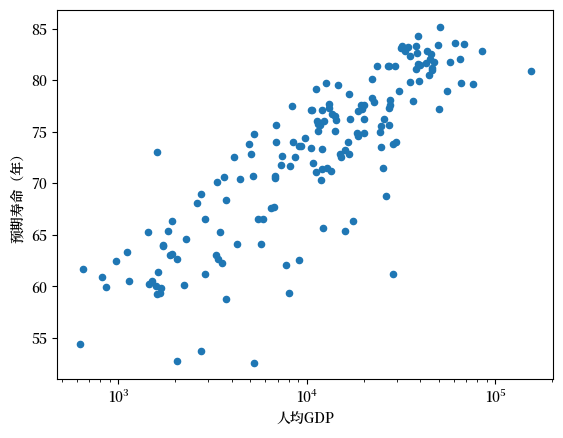
通过指定 logx 你可以在对数尺度上绘制人均GDP数据

df.plot(x='gdppc', y='life_expectancy', kind='scatter',  xlabel="人均GDP", ylabel="预期寿命（年）", logx=True);

_images/2afe42f3eff5cd374569030663c50ded6aa924aa677b07cd6e36dd48913f3f49.png

从这次转换可以看出，线性模型更贴近数据的形状。

df['log_gdppc'] = df['gdppc'].apply(np.log10)

df

	cntry	year	life_expectancy	gdppc	log_gdppc
0	AFG	2018	63.1	1934.5550	3.286581
1	ALB	2018	79.2	11104.1660	4.045486
2	DZA	2018	76.1	14228.0250	4.153145
3	AGO	2018	62.1	7771.4420	3.890502
4	ARG	2018	77.0	18556.3830	4.268493
...	...	...	...	...	...
161	VNM	2018	74.0	6814.1420	3.833411
162	OWID_WRL	2018	72.6	15212.4150	4.182198
163	YEM	2018	64.6	2284.8900	3.358865
164	ZMB	2018	62.3	3534.0337	3.548271
165	ZWE	2018	61.4	1611.4052	3.207205

166 rows × 5 columns

第4问: 使用 (44.1) 和 (44.2) 来计算 $α$ 和 $β$ 的最优值

data = df[['log_gdppc', 'life_expectancy']].copy()  # 从DataFrame中提取数据

# 计算样本均值
x_bar = data['log_gdppc'].mean()
y_bar = data['life_expectancy'].mean()

data

	log_gdppc	life_expectancy
0	3.286581	63.1
1	4.045486	79.2
2	4.153145	76.1
3	3.890502	62.1
4	4.268493	77.0
...	...	...
161	3.833411	74.0
162	4.182198	72.6
163	3.358865	64.6
164	3.548271	62.3
165	3.207205	61.4

166 rows × 2 columns

# 计算求和
data['num'] = data['log_gdppc'] * data['life_expectancy'] - y_bar * data['log_gdppc']
data['den'] = pow(data['log_gdppc'],2) - x_bar * data['log_gdppc']
β = data['num'].sum() / data['den'].sum()
print(β)

12.643730292819708

α = y_bar - β * x_bar
print(α)

21.70209670138904

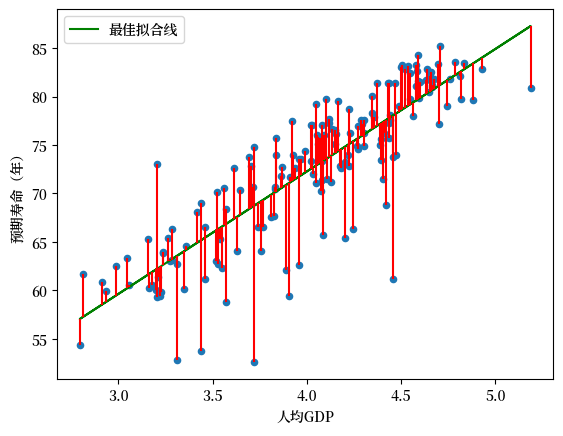
第5问: 绘制使用 OLS 找到的最佳拟合线

data['life_expectancy_hat'] = α + β * df['log_gdppc']
data['error'] = data['life_expectancy_hat'] - data['life_expectancy']

fig, ax = plt.subplots()
data.plot(x='log_gdppc',y='life_expectancy', kind='scatter', ax=ax, xlabel="人均GDP", ylabel="预期寿命（年）")
data.plot(x='log_gdppc',y='life_expectancy_hat', kind='line', ax=ax, color='g', xlabel="人均GDP", label="最佳拟合线")
plt.vlines(data['log_gdppc'], data['life_expectancy_hat'], data['life_expectancy'], color='r')

<matplotlib.collections.LineCollection at 0x7f2601172810>

_images/7263b0d93b150584ac85c2010cf8731c8adfb863ae775b11d0deae8c4610f93e.png

Exercise 44.2

最小化平方和并不是生成最佳拟合线的唯一方法。

举个例子，我们还可以考虑最小化 绝对值 之和，这样可以减少对异常值的权重。

使用最小绝对值法求解 $α$ 和 $β$

44. 简单线性回归模型#

44.1. 残差相对于 α 和 β 是如何变化的#

44.2. 计算最优值#

44.1. 残差相对于 $α$ 和 $β$ 是如何变化的#