20. 蒙特卡罗方法与期权定价#

20.1. 概览#

通过以下方式，我们可以进行简单的概率计算：

用笔和纸，
查询著名的概率分布，
逻辑推理。

例如，我们可以轻松地计算出：

一枚普通的硬币，抛五次中出现三次正面的概率
一个随机变量的期望值，如果这一随机变量有 $1 / 2$ 的概率等于 $- 10$ ，有 $1 / 2$ 的概率等于 $100$ 。

但是，有些概率计算非常复杂。

在经济和金融问题中，经常需要计算复杂的概率和期望值。

处理复杂概率计算，最重要的工具之一是蒙特卡罗方法。

在本节讲座中，我们将介绍如何使用蒙特卡罗方法计算期望值，以及其在金融中的应用。

以下是必要的模块导入：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from numpy.random import randn

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

20.2. 蒙特卡罗简介#

在本小节中，我们将描述如何使用蒙特卡罗方法计算期望值。

20.2.1. 给定分布的股票价格#

假设我们正在考虑购买某公司的股票。

我们的计划是：

现在买入股票，持有一年后再卖出，或者
用我们的钱做其他事情。

首先，我们将一年后的股票价格视为一个随机变量 $S$ 。

在决定是否购买股票之前，我们需要知道 $S$ 分布的一些特性。

例如，假设 $S$ 的均值相对于购买股票的价格很高。

这表明我们很有机会以相对较高的价格卖出。

但是，假设 $S$ 的方差也很高。

这表明购买股票有风险，我们或许应该放弃买入。

不论何种方式，上述讨论说明理解 $S$ 的分布的重要性。

假设，在分析数据后，我们猜想 $S$ 很好地由参数为 $μ, σ$ 的对数正态分布表示。

$S$ 与 $\exp (μ + σ Z)$ 分布相同，其中 $Z$ 符合标准正态分布。
我们将此记作 $S \sim L N (μ, σ)$ 。

所有关于统计的优质参考资料（如百度百科）都会告诉我们，其均值和方差为

E S = \exp (μ + \frac{σ^{2}}{2})

和

Var S = [\exp (σ^{2}) - 1] \exp (2 μ + σ^{2})

至此，我们还不需要使用计算机。

20.2.2. 未知分布的股票价格#

假设我们希望更仔细地研究股票价格 $S$ 的分布。

我们假设股票价格取决于三个变量， $X_{1}$ 、 $X_{2}$ 和 $X_{3}$ （例如，销售额、通货膨胀和利率）。

具体而言，我们的研究发现：

S = (X_{1} + X_{2} + X_{3})^{p}

其中：

$p$ 是一个已知的正数（即已被估计），
$X_{i} \sim L N (μ_{i}, σ_{i})$ ，当 $i = 1, 2, 3$ 时，
$μ_{i}, σ_{i}$ 的值也是已知的，
随机变量 $X_{1}$ 、 $X_{2}$ 和 $X_{3}$ 是相互独立的。

我们应该如何计算 $S$ 的均值？

仅仅依靠纸笔进行计算是十分困难的（除了 $p = 1$ ）。

但幸运地，我们至少有一种简便的方法可以近似地做到。

这就是蒙特卡洛方法，其操作步骤如下：

在计算机上生成 $n$ 次独立抽取的 $X_{1}$ 、 $X_{2}$ 和 $X_{3}$ ，
使用这些抽取值生成 $n$ 次独立抽取的 $S$ ，
取这些 $S$ 的抽取值的平均值。

当 $n$ 很大时，这个平均值将接近真实的平均值。

这归因于大数定律，我们在大数定律与中心极限定理中讨论过。

我们为 $p$ 和每个 $μ_{i}$ 和 $σ_{i}$ 使用以下赋值。

n = 1_000_000
p = 0.5
μ_1, μ_2, μ_3 = 0.2, 0.8, 0.4
σ_1, σ_2, σ_3 = 0.1, 0.05, 0.2

20.2.2.1. 使用Python循环的一种例程#

这里是一个使用Python原生循环，计算期望平均值的例程

\frac{1}{n} \sum_{i = 1}^{n} S_{i} \approx E S

%%time

S = 0.0
for i in range(n):
    X_1 = np.exp(μ_1 + σ_1 * randn())
    X_2 = np.exp(μ_2 + σ_2 * randn())
    X_3 = np.exp(μ_3 + σ_3 * randn())
    S += (X_1 + X_2 + X_3)**p
S / n

CPU times: user 3.6 s, sys: 374 μs, total: 3.6 s
Wall time: 3.6 s

2.2298508051994723

我们还可以构建一个包含这些操作的函数：

def compute_mean(n=1_000_000):
    S = 0.0
    for i in range(n):
        X_1 = np.exp(μ_1 + σ_1 * randn())
        X_2 = np.exp(μ_2 + σ_2 * randn())
        X_3 = np.exp(μ_3 + σ_3 * randn())
        S += (X_1 + X_2 + X_3)**p
    return (S / n)

现在调用函数。

compute_mean()

2.2296626299188866

20.2.3. 一种向量化的例程#

如果我们想要更准确的估计，我们应该增加 $n$ 的大小。

但是上面的代码运行速度相当慢。

为了让它运行更快，我们使用 NumPy 来实现向量化例程。

def compute_mean_vectorized(n=1_000_000):
    X_1 = np.exp(μ_1 + σ_1 * randn(n))
    X_2 = np.exp(μ_2 + σ_2 * randn(n))
    X_3 = np.exp(μ_3 + σ_3 * randn(n))
    S = (X_1 + X_2 + X_3)**p
    return S.mean()

%%time

compute_mean_vectorized()

CPU times: user 82.1 ms, sys: 4 ms, total: 86.1 ms
Wall time: 86 ms

2.2297498102917945

我们注意到这个例程运行起来快得多。

我们可以通过增加 $n$ 来提高精度，但仍保持合理的速度：

%%time

compute_mean_vectorized(n=10_000_000)

CPU times: user 792 ms, sys: 51 ms, total: 843 ms
Wall time: 843 ms

2.2297405015135836

20.3. 利用风险中性定价欧式看涨期权#

接下来，我们将在风险中性的假设下对欧式看涨期权进行定价。

首先我们将讨论风险中性，然后考虑欧式期权。

20.3.1. 风险中性定价#

当我们使用风险中性定价时，我们根据给定资产的预期收益来决定其价格：

成本 = 预期收益

例如，假设有人承诺在抛硬币中支付你

1,000,000 美元，如果结果为正面
0 美元，如果结果为反面

我们将受益记作 $G$ , 则

P {G = 10^{6}} = P {G = 0} = \frac{1}{2}

假设除此之外，你可以将这一承诺卖给任何需要它的人。

首先他们要支付给你 $P$ ，即你的销售价格
然后他们获得 $G$ ，可能是1,000,000 或者0。

那这一资产（这个承诺）的价格定为多少，是公平的？

“公平”的定义是模糊的，但我们可以说它的 风险中性价格是50万美元。

这是因为风险中性价格仅仅是资产的预期收益，即

E G = \frac{1}{2} \times 10^{6} + \frac{1}{2} \times 0 = 5 \times 10^{5}

20.3.2. 关于风险的提示#

如名称所示，风险中性定价不考虑风险。

要理解这一点，思考你是否愿意为这样一个承诺支付500,000美元。

你是更愿意收到确定的500,000美元，还是有50%的概率收到1,000,000美元，而另外50%的概率空手而归？

至少一些读者会偏好第一种选择——尽管有些人可能更喜欢第二种。

这让我们意识到500,000美元并不一定是“正确”的价格——或者，如果市场上有这样的承诺，我们会见到的价格。

尽管如此，风险中性价格是一个重要的基准，经济学家和金融市场参与者每天都在试图计算它。

20.3.3. 贴现#

在之前的讨论中，我们还忽略了时间因素。

一般来说，现在收到 $x$ 美元比在 $n$ 个周期后（例如10年）收到 $x$ 美元更好。

毕竟，如果我们现在就收到 $x$ 美元，我们可以将其存入银行中，按照利率 $r > 0$ 计算，在 $n$ 个周期后会收到 $(1 + r)^{n} x$ 。

因此，我们在考虑现值时需要对未来的现金流进行贴现。

这可以通过以下方式实现：

将未来一期的付款乘以 $β < 1$
将未来 $n$ 期的付款乘以 $β^{n}$ ，以此类推。

对于刚才描述的“承诺”，我们的风险中性价格也同样需要进行调整。

因此，如果 $G$ 在 $n$ 个周期后实现，那么风险中性价格为：

P = β^{n} E G = β^{n} 5 \times 10^{5}

20.3.4. 欧式看涨期权#

现在，我们来计算欧式看涨期权的价格。

期权有三个要素：

$n$ , 到期日，
$K$ , 行权价格，
$S_{n}$ , 在日期 $n$ 的标的资产价格。

例如，假设标的资产是亚马逊的一股股票。

那么该期权的持有者，有权在 $n$ 天后以 $K$ 价格买入亚马逊的一股股票。

如果 $S_{n} > K$ ，那么持有者将会行使期权，以 $K$ 的价格买入，再以 $S_{n}$ 的价格卖出，从而获得 $S_{n} - K$ 的利润。

如果 $S_{n} \leq K$ ，那么持有者将不会行使期权，收益为零。

因此，收益为 $max {S_{n} - K, 0}$ 。

在风险中性假设下，期权的价格是折现后的期望收益：

P = β^{n} E max {S_{n} - K, 0}

我们要假定 $S_{n}$ 的分布，从而计算期望。

假设 $S_{n} \sim L N (μ, σ)$ ，且 $μ$ 和 $σ$ 是已知的。

如果 $S_{n}^{1}, \dots, S_{n}^{M}$ 是从这个对数正态分布中独立抽取的，则根据大数定律，

E max {S_{n} - K, 0} \approx \frac{1}{M} \sum_{m = 1}^{M} max {S_{n}^{m} - K, 0}

假设

μ = 1.0
σ = 0.1
K = 1
n = 10
β = 0.95

设置模拟次数为

M = 10_000_000

以下是计算该期权价格的代码

S = np.exp(μ + σ * np.random.randn(M))
return_draws = np.maximum(S - K, 0)
P = β**n * np.mean(return_draws)
print(f"蒙特卡洛期权价格约为 {P:3f}")

蒙特卡洛期权价格约为 1.036953

20.4. 通过动态模型定价#

在这个练习中，我们将研究一个更符合实际的模型，来描述股票价格 $S_{n}$ 。

这需要假定股票价格的底层动态。

首先我们假定动态变化机制。

然后我们将使用蒙特卡洛方法计算期权的价格。

20.4.1. 简单动态#

对于 ${S_{t}}$ ，一个简单的模型是

\ln \frac{S_{t + 1}}{S_{t}} = μ + σ ξ_{t + 1}

其中

$S_{0}$ 是对数正态分布的，
${ξ_{t}}$ 是独立同分布的标准正态分布。

在上述假设下， $S_{n}$ 是对数正态分布的。

这是因为，不妨使得 $s_{t} := \ln S_{t}$ ，注意到价格动态可以写成

(20.1)#

s_{t + 1} = s_{t} + μ + σ ξ_{t + 1}

由于 $s_{0}$ 是正态分布的且 $ξ_{1}$ 是独立同分布的正态分布，所以 $s_{1}$ 是正态分布的。

通过迭代可以发现 $s_{n}$ 是符合正态分布的。

因此 $S_{n} = \exp (s_{n})$ 是符合对数正态分布的。

20.4.2. 简单动态问题#

上述的简单动态模型可以轻松地计算出 $S_{n}$ 的分布。

然而，它的预测是反事实的，因为在现实世界中，波动率（由 $σ$ 测量）并不是平稳的。

相反地，它随时间变化而变化，时而高（如在全球金融危机期间），时而低。

因此，这意味着 $σ$ 不应该是常数。

20.4.3. 更加贴合实际的动态模型#

这促使我们去研究改好的版本：

\ln \frac{S_{t + 1}}{S_{t}} = μ + σ_{t} ξ_{t + 1}

其中

σ_{t} = \exp (h_{t}), h_{t + 1} = ρ h_{t} + ν η_{t + 1}

这里的 ${η_{t}}$ 也是独立同分布且标准正态的。

20.4.4. 默认参数#

对于动态模型，我们采用以下参数值。

default_μ  = 0.0001
default_ρ  = 0.1
default_ν  = 0.001
default_S0 = 10
default_h0 = 0

（这里default_S0 是 $S_{0}$ ，default_h0 是 $h_{0}$ 。）

对于期权，我们使用以下作为默认值。

default_K = 100
default_n = 10
default_β = 0.95

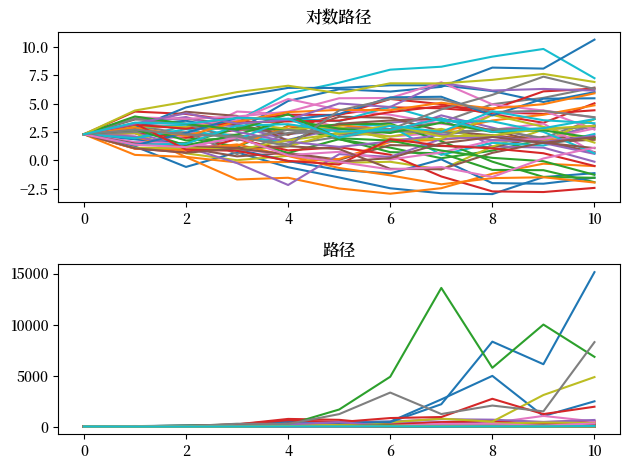
20.4.5. 可视化#

令 $s_{t} := \ln S_{t}$ ，价格动态可写为

s_{t + 1} = s_{t} + μ + \exp (h_{t}) ξ_{t + 1}

以下是使用这个方程模拟路径的函数：

def simulate_asset_price_path(μ=default_μ, S0=default_S0, h0=default_h0, n=default_n, ρ=default_ρ, ν=default_ν):
    s = np.empty(n+1)
    s[0] = np.log(S0)

    h = h0
    for t in range(n):
        s[t+1] = s[t] + μ + np.exp(h) * randn()
        h = ρ * h + ν * randn()

    return np.exp(s)

这里我们绘制路径及其对数。

fig, axes = plt.subplots(2, 1)

titles = '对数路径', '路径'
transforms = np.log, lambda x: x
for ax, transform, title in zip(axes, transforms, titles):
    for i in range(50):
        path = simulate_asset_price_path()
        ax.plot(transform(path))
    ax.set_title(title)

fig.tight_layout()
plt.show()

_images/b4cdddaab5d16b4b4b4b7246bf9b914b8ace4ef20443a870b02400ebd0ac58fd.png

20.4.6. 计算价格#

因为我们的模型更加复杂，我们难以轻易确定 $S_{n}$ 的分布。

所以为了计算期权的价格 $P$ ，我们使用蒙特卡洛方法。

我们计算每一次抽样 $S_{n}^{1}, \dots, S_{n}^{M}$ 的平均值 $S_{n}$ ，并诉诸大数法则：

E max {S_{n} - K, 0} \approx \frac{1}{M} \sum_{m = 1}^{M} max {S_{n}^{m} - K, 0}

以下版本借助了Python 循环。

def compute_call_price(β=default_β,
                       μ=default_μ,
                       S0=default_S0,
                       h0=default_h0,
                       K=default_K,
                       n=default_n,
                       ρ=default_ρ,
                       ν=default_ν,
                       M=10_000):
    current_sum = 0.0
    # 对每一个样本路径
    for m in range(M):
        s = np.log(S0)
        h = h0
        # 模拟时间前进
        for t in range(n):
            s = s + μ + np.exp(h) * randn()
            h = ρ * h + ν * randn()
        # 并将值 max{S_n - K, 0} 加到 current_sum
        current_sum += np.maximum(np.exp(s) - K, 0)

    return β**n * current_sum / M

%%time
compute_call_price()

CPU times: user 189 ms, sys: 0 ns, total: 189 ms
Wall time: 189 ms

804.7625547225585

20.5. 练习#

Exercise 20.1

我们想要在上面的代码中增加 $M$ ，使得计算更加精确。

但是这存在问题，因为这让Python循环运行速度十分缓慢。

你的任务是使用NumPy编写一个更快的版本。

Solution to Exercise 20.1

def compute_call_price_vector(β=default_β,
                       μ=default_μ,
                       S0=default_S0,
                       h0=default_h0,
                       K=default_K,
                       n=default_n,
                       ρ=default_ρ,
                       ν=default_ν,
                       M=10_000):

    s = np.full(M, np.log(S0))
    h = np.full(M, h0)
    for t in range(n):
        Z = np.random.randn(2, M)
        s = s + μ + np.exp(h) * Z[0, :]
        h = ρ * h + ν * Z[1, :]
    expectation = np.mean(np.maximum(np.exp(s) - K, 0))

    return β**n * expectation

%%time
compute_call_price_vector()

CPU times: user 4.87 ms, sys: 947 μs, total: 5.81 ms
Wall time: 5.21 ms

690.0136554611593

注意到，这个版本的速度比使用Python循环的版本要快。

现在让我们尝试更大的 $M$ 以获得更准确的计算。

%%time
compute_call_price(M=10_000_000)

CPU times: user 3min 11s, sys: 32.9 ms, total: 3min 11s
Wall time: 3min 11s

841.2349730479339

Exercise 20.2

设想一种欧式看涨期权，该期权的标的资产现货价格为100美元，有一个120美元的敲出障碍。

这种期权在各方面都类似于普通的欧式看涨期权，但是，一旦标的资产现货价格超过120美元，期权便会被”敲出”，合约即刻失效。

注意，如果现货价格再次跌破120美元，期权不会重新激活。

使用在(20.1)问题中定义的动态，定价这个欧式看涨期权。

Solution to Exercise 20.2

default_μ  = 0.0001
default_ρ  = 0.1
default_ν  = 0.001
default_S0 = 10
default_h0 = 0
default_K = 100
default_n = 10
default_β = 0.95
default_bp = 120

def compute_call_price_with_barrier(β=default_β,
                                    μ=default_μ,
                                    S0=default_S0,
                                    h0=default_h0,
                                    K=default_K,
                                    n=default_n,
                                    ρ=default_ρ,
                                    ν=default_ν,
                                    bp=default_bp,
                                    M=50_000):
    current_sum = 0.0
    # 对每个样本路径进行模拟
    for m in range(M):
        s = np.log(S0)
        h = h0
        payoff = 0
        option_is_null = False
        # 模拟时间发展
        for t in range(n):
            s = s + μ + np.exp(h) * randn()
            h = ρ * h + ν * randn()
            if np.exp(s) > bp:
                payoff = 0
                option_is_null = True
                break

        if not option_is_null:
            payoff = np.maximum(np.exp(s) - K, 0)
        # 将payoff加入到current_sum中
        current_sum += payoff

    return β**n * current_sum / M

%time compute_call_price_with_barrier()

CPU times: user 1.1 s, sys: 0 ns, total: 1.1 s
Wall time: 1.1 s

0.04020204505593266

再看向量化版本，这比使用Python循环快。

def compute_call_price_with_barrier_vector(β=default_β,
                                           μ=default_μ,
                                           S0=default_S0,
                                           h0=default_h0,
                                           K=default_K,
                                           n=default_n,
                                           ρ=default_ρ,
                                           ν=default_ν,
                                           bp=default_bp,
                                           M=50_000):
    s = np.full(M, np.log(S0))
    h = np.full(M, h0)
    option_is_null = np.full(M, False)
    for t in range(n):
        Z = np.random.randn(2, M)
        s = s + μ + np.exp(h) * Z[0, :]
        h = ρ * h + ν * Z[1, :]
        # 标记所有股价高于敲出障碍价格的期权为无效
        option_is_null = np.where(np.exp(s) > bp, True, option_is_null)

    # 在option_is_null的索引处将payoff标记为0
    payoff = np.where(option_is_null, 0, np.maximum(np.exp(s) - K, 0))
    expectation = np.mean(payoff)
    return β**n * expectation

%time compute_call_price_with_barrier_vector()

CPU times: user 28.6 ms, sys: 0 ns, total: 28.6 ms
Wall time: 28.4 ms

0.04199671298643371