28. 通过货币资助的政府赤字和价格水平#

28.1. 概览#

本讲座在货币主义价格水平理论模型的基础上进行了扩展，主要通过修改控制货币供应的运动法则。

我们的模型由两个核心部分组成：

货币需求函数
货币供应的运动法则

货币需求函数描述了公众对”实际余额”的需求，也就是名义货币余额与价格水平的比率：

当期的实际余额需求与公众预期的通货膨胀率呈反比关系
我们假设公众能够完美预测通货膨胀率

货币供应的运动法则则表明政府通过印发新货币来为其支出提供资金

在我们的模型中，对于每个时间点$t \geq 0$，货币的需求与供给处于平衡状态。

需求与供应之间的平衡形成了一个动态模型，在该模型中，货币供应和价格水平序列通过一组同时线性方程来同时决定。

这些方程通常被称为向量线性差分方程。

在本讲座中，我们将通过两种不同的方法来求解这些方程。

(解决向量线性差分方程的一种方法将利用在这个讲座特征值和特征向量中研究的矩阵分解。)

在本讲座中，我们将遇到以下宏观经济学概念：

政府通过发行纸币或电子货币征收通货膨胀税
通货膨胀税率的动态拉弗曲线中存在两个静止均衡点
在理性预期下的反常动力学中，系统趋向于较高的静止通货膨胀税率
在对静态通货膨胀率进行比较静态分析时，我们得到一特殊结果：可以通过维持更高的政府赤字来降低通货膨胀，例如通过加印货币来筹集更多资源。

在这个讲座通货膨胀税的拉弗曲线中研究了模型的非线性版本，同样的定性结果也普遍存在。

这些结果为将在这个讲座拉弗曲线与自适应预期中呈现的分析奠定了基础，它研究了当前模型的非线性版本；它假定了一种“适应性预期”的版本，而不是理性预期。

那个讲座将探讨：

通货膨胀率的两个静止均衡点保持不变，用适应性预期替代理性预期，但是 $\ldots$
此模型违反了反常动力学因为它收敛的静止通货膨胀率比通常的系统较低
出现了一种更可信的比较动态结果，即现在可以通过降低政府赤字来降低通货膨胀我们将在讲座一些不愉快的货币主义算术使用这个结论来分析选择一个平稳通胀率的合理性。

我们将使用这些线性代数工具：

矩阵乘法
矩阵求逆
矩阵的特征值和特征向量

28.2. 货币的需求与供给#

我们使用复数形式”demands”（需求）和”supplies”（供给），是因为在每个时间点$t \geq 0$都存在相应的货币需求和供给。

让我们定义以下变量：

$m_{t+1}$ 表示时间点 $t$ 结束时的货币供给
$m_{t}$ 表示从上一时期 $t-1$ 带入到当前时期 $t$ 的货币供给
$g$ 表示政府在 $t \geq 1$ 时通过印钞方式融资的赤字
$m_{t+1}^d$ 表示在时间 $t$ 对下一期 $t+1$ 的货币需求
$p_t$ 表示时间 $t$ 的价格水平
$b_t = \frac{m_{t+1}}{p_t}$ 表示时间 $t$ 结束时的实际货币余额
$R_t = \frac{p_t}{p_{t+1}}$ 表示从时间 $t$ 到 $t+1$ 持有货币的实际回报率

为了更好地理解各变量的含义，我们来看看它们的度量单位：

$m_t$ 和 $m_t^d$ 以美元计量
$g$ 以时间 $t$ 的商品数量计量
$p_t$ 以每单位商品的美元价格计量
$R_t$ 表示持有货币的实际回报率，即时间 $t$ 的商品与时间 $t+1$ 的商品之比
$b_t$ 以时间 $t$ 的商品数量计量

接下来，我们需要确定货币的需求和供给函数。

对于货币需求，我们采用类似凯根（Cagan）的需求函数

(28.1)#\[ \frac{m_{t+1}^d}{p_t}=\gamma_1 - \gamma_2 \frac{p_{t+1}}{p_t}, \quad t \geq 0 \]

其中 $\gamma_1, \gamma_2$ 是正参数。

现在我们转向货币供给。

我们假设 $m_0 >0$ 是模型外部决定的“初始条件”。

我们将 $m_0$ 设定为一个任意的正值，比如说 $100。

对于 $ t \geq 1$时，我们假设货币供给由政府的预算约束决定

(28.2)#\[ m_{t+1} - m_{t} = p_t g , \quad t \geq 0 \]

根据这个方程，政府每个时期通过印钞来为购买 $g$ 单位商品的支出提供资金。

在均衡状态下，货币需求必须等于货币供给：

(28.3)#\[ m_{t+1}^d = m_{t+1}, \quad t \geq 0 \]

让我们思考一下方程(28.3)的含义。

时间 $t$ 的货币需求取决于 $t$ 时期和 $t+1$ 时期的价格水平。

而时间 $t+1$ 的货币供给则由 $t$ 时期的货币供给和价格水平决定。

因此，从 $t \geq 0$ 开始的均衡条件(28.3)表明，价格序列 $\{p_t\}_{t=0}^\infty$ 和货币供给序列 $\{m_t\}_{t=0}^\infty$ 是相互关联的，它们必须共同确定。

28.3. 均衡价格和货币供应序列#

基于上述条件，我们可以推导出对于 $t \geq 1$，实际货币余额的演变遵循以下规律：

\[ \frac{m_{t+1}}{p_t} - \frac{m_{t}}{p_{t-1}} \frac{p_{t-1}}{p_t} = g \]

或

(28.4)#\[ b_t - b_{t-1} R_{t-1} = g \]

对实际余额的需求为：

(28.5)#\[ b_t = \gamma_1 - \gamma_2 R_t^{-1} . \]

我们将关注参数值和与之相关的实际余额的毛收益率，确保实际余额的需求为正值。

根据(28.5) 这意味着：

\[ b_t = \gamma_1 - \gamma_2 R_t^{-1} > 0 \]

这说明了：

(28.6)#\[ R_t \geq \left( \frac{\gamma_2}{\gamma_1} \right) \equiv \underline R \]

$\underline R$ 是支撑非负实际余额需求的货币回报的最小毛实际收益率。

我们将描述两种紧密相关但又存在区别的方法来计算价格水平和货币供应的序列 $\{p_t, m_t\}_{t=0}^\infty$。

但首先，我们介绍一种特殊的均衡状态，称为稳态。

在稳态均衡下，一些关键变量随时间保持恒定或不变，而其余变量可以表示为这些常量的函数。

找到这样的状态变量在某种程度上是一门艺术。

在许多模型中，寻找这种不变变量的一个好的方法是在比率中寻找。

这个技巧在当前模型中也是成立的。

28.3.1. 稳态#

在我们研究的模型中的稳态均衡，

\[ \begin{aligned} R_t & = \bar R \cr b_t & = \bar b \end{aligned} \]

对于 $t \geq 0$。

注意 $R_t = \frac{p_t}{p_{t+1}}$ 和 $b_t = \frac{m_{t+1}}{p_t} $ 都是比率。

为了计算稳态，我们寻找满足政府预算约束和实际货币余额需求函数的稳态版本的货币和实际余额的毛收益率 $\bar R, \bar b$：

\[ \begin{aligned} g & = \bar b ( 1 - \bar R) \cr \bar b & = \gamma_1- \gamma_2 \bar R^{-1} \end{aligned} \]

组合这些方程得到

(28.7)#\[ (\gamma_1 + \gamma_2) - \frac{\gamma_2}{\bar R} - \gamma_1 \bar R = g \]

左侧是政府通过支付货币的毛收益率（$\bar R \le 1$）收集的稳态时的铸币税或政府收入。

右侧是政府支出。

定义稳态铸币税为

(28.8)#\[ S(\bar R) = (\gamma_1 + \gamma_2) - \frac{\gamma_2}{\bar R} - \gamma_1 \bar R \]

注意 $S(\bar R) \geq 0$ 仅当 $\bar R \in [\frac{\gamma_2}{\gamma_1}, 1] \equiv [\underline R, \overline R]$，同时当 $\bar R = \underline R$ 或 $\bar R = \overline R$ 时，$S(\bar R) = 0$。

我们将研究满足此条件的均衡序列

\[ R_t \in [\underline R, \overline R], \quad t \geq 0. \]

通过 $\bar R$最大化稳态铸币税 (28.8) ，我们发现货币的最大化回报率是

\[ \bar R_{\rm max} = \sqrt{\frac{\gamma_2}{\gamma_1}} \]

据此，政府通过印钞可以收集的最大铸币税收入是

\[ (\gamma_1 + \gamma_2) - \frac{\gamma_2}{\bar R_{\rm max}} - \gamma_1 \bar R_{\rm max} \]

将方程 (28.7) 重新写为

(28.9)#\[ -\gamma_2 + (\gamma_1 + \gamma_2 - g) \bar R - \gamma_1 \bar R^2 = 0 \]

二次方程 (28.9)的解就是稳态毛收益率 $\bar R$。

所以通常存在两个稳态。

28.4. 一些代码#

让我们从一些导入代码开始:

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
plt.rcParams['figure.dpi'] = 300
from collections import namedtuple

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

让我们设定参数并计算货币的可能稳态回报率 $\bar R$ 和铸币税最大货币收益率，以及我们稍后讨论的与货币最大稳态回报率相关联的初始价格水平 $p_0$。

首先，我们创建一个 namedtuple 来存储参数，以便我们可以在整个讲座中的函数中重复使用这个 namedtuple。

# 创建一个包含参数的 namedtuple
MoneySupplyModel = namedtuple("MoneySupplyModel", 
                        ["γ1", "γ2", "g", 
                         "M0", "R_u", "R_l"])

def create_model(γ1=100, γ2=50, g=3.0, M0=100):
    
    # 计算 R 的稳态
    R_steady = np.roots((-γ1, γ1 + γ2 - g, -γ2))
    R_u, R_l = R_steady
    print("[R_u, R_l] =", R_steady)
    
    return MoneySupplyModel(γ1=γ1, γ2=γ2, g=g, M0=M0, R_u=R_u, R_l=R_l)

现在我们计算 $\bar R_{\rm max}$ 和对应的收益

def seign(R, model):
    γ1, γ2, g = model.γ1, model.γ2, model.g
    return -γ2/R + (γ1 + γ2)  - γ1 * R

msm = create_model()

# 计算 p0 的初始猜测
p0_guess = msm.M0 / (msm.γ1 - msm.g - msm.γ2 / msm.R_u)
print(f'p0 猜测 = {p0_guess:.4f}')

# 计算最大化铸币税的回报率
R_max = np.sqrt(msm.γ2/msm.γ1)
g_max = seign(R_max, msm)
print(f'R_max, g_max = {R_max:.4f}, {g_max:.4f}')

[R_u, R_l] = [0.93556171 0.53443829]
p0 猜测 = 2.2959
R_max, g_max = 0.7071, 8.5786

现在我们来把铸币税作为 $R$ 的潜在稳定值的函数并绘制函数图像。

我们将看到有两个 $R$ 的稳态值达到了 $g$ 的铸币税水平，其中一个记为 $R_\ell$，另一个记为 $R_u$。

它们满足 $R_\ell < R_u$ 并且与更高的通货膨胀税率 $(1-R_\ell)$ 和较低的通货膨胀税率 $1 - R_u$ 关联。

# 生成 R 的值
R_values = np.linspace(msm.γ2/msm.γ1, 1, 250)

# 计算函数值
seign_values = seign(R_values, msm)

# 将 seign_values 与 R 值进行可视化
fig, ax = plt.subplots(figsize=(11, 5))
plt.plot(R_values, seign_values, label='通货膨胀税收益')
plt.axhline(y=msm.g, color='red', linestyle='--', label='政府赤字')
plt.xlabel('$R$')
plt.ylabel('铸币税')

plt.legend()
plt.show()

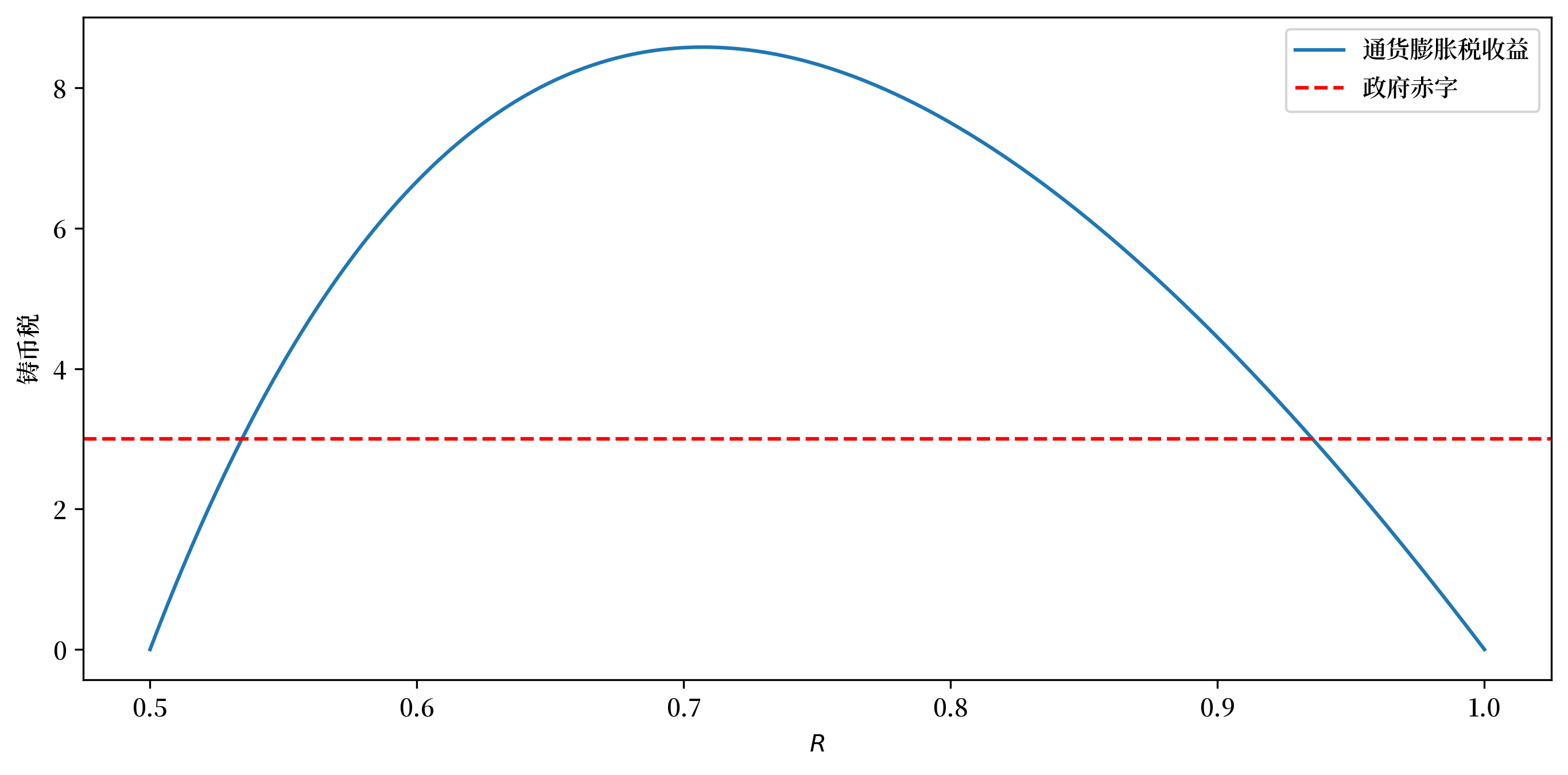
_images/329778743931e17f349b172c47802f9ee8b32c08752cc514b105412db3073dbc.png — Fig. 28.1 以稳态回报率货币为x画出稳态时通胀税收益的函数（实线蓝色曲线）和实际政府支出（虚线红色线）来对比#

让我们显示出两个稳态回报率 $\bar R$ 和政府收集的相关铸币税收入。

（构造上，两个稳态回报率应该产生相同金额的实际收入。）

我们希望接下来的代码能确认这一点。

g1 = seign(msm.R_u, msm)
print(f'R_u, g_u = {msm.R_u:.4f}, {g1:.4f}')

g2 = seign(msm.R_l, msm)
print(f'R_l, g_l = {msm.R_l:.4f}, {g2:.4f}')

R_u, g_u = 0.9356, 3.0000
R_l, g_l = 0.5344, 3.0000

现在让我们计算印钞所能获得的最大稳态铸币税收入，以及实现这一最大收入时对应的稳态货币回报率。

28.5. 两种计算均衡的策略#

接下来，我们将计算模型的均衡解，这些均衡不一定是稳态。

为此，我们将探讨两种不同的计算方法。

28.5.1. 方法 1#

首先选择初始货币回报率 $R_0 \in [\frac{\gamma_2}{\gamma_1}, R_u]$，然后计算对应的初始实际货币余额 $b_0 = \gamma_1 - \gamma_2/R_0$。
接着，通过递归求解下面的方程组，计算均衡路径上的回报率和实际余额序列 $\{R_t, b_t\}_{t=1}^\infty$。对于 $t \geq 1$，我们依次求解方程 (28.4) 和 (28.5)：

(28.10)#\[ \begin{aligned} b_t & = b_{t-1} R_{t-1} + g \cr R_t^{-1} & = \frac{\gamma_1}{\gamma_2} - \gamma_2^{-1} b_t \end{aligned} \]

据此构建对应均衡 $p_0$

(28.11)#\[ p_0 = \frac{m_0}{\gamma_1 - g - \gamma_2/R_0} \]

按顺序求解以下方程后计算得出 $\{p_t, m_t\}_{t=1}^\infty$

(28.12)#\[ \begin{aligned} p_t & = R_t p_{t-1} \cr m_t & = b_{t-1} p_t \end{aligned} \]

Remark 28.1

方法 1 采用间接计算均衡的策略：先求解货币回报率和实际余额的均衡序列 $\{R_t, b_t\}_{t=0}^\infty$，然后基于这些结果推导出价格水平和名义货币量的均衡序列 $\{p_t, m_t\}_{t=0}^\infty$。

Remark 28.2

需要注意的是，方法 1 要求我们首先从区间 $[\frac{\gamma_2}{\gamma_1}, R_u]$ 中选择一个初始条件 $R_0$。

这意味着均衡序列 $\{p_t, m_t\}_{t=0}^\infty$ 并不是唯一的。

事实上，根据不同的 $R_0$ 选择，我们可以得到一个连续的均衡族。

Remark 28.3

每个初始货币回报率 $R_0$ 都对应着一个唯一的初始价格水平 $p_0$，这种对应关系由方程 (28.11) 给出。

28.5.2. 方法2#

方法2采用更直接的计算方式。

我们首先定义状态向量 $y_t = \begin{bmatrix} m_t \cr p_t\end{bmatrix}$，它包含了名义货币量和价格水平。

然后，我们可以将均衡条件 (28.1)、(28.2) 和 (28.3) 整合为一个简洁的一阶向量差分方程：

\[ y_{t+1} = M y_t, \quad t \geq 0 \]

在这个框架下，我们需要指定初始状态 $y_0 = \begin{bmatrix} m_0 \cr p_0 \end{bmatrix}$ 作为计算的起点。

解出的结果是

\[ y_t = M^t y_0. \]

现在让我们思考初始条件 $y_0$。

自然地，我们会将已知的初始货币存量 $m_0 > 0$ 作为初始条件的一部分。

但对于 $p_0$ 应该如何确定呢？

我们期望模型能够自行决定这个值，不是吗？

确实如此，但问题在于可能存在多个与均衡相容的初始价格水平 $p_0$。

事实上，我们很快就会看到，在方法2中选择初始价格水平 $p_0$ 与在方法1中选择初始货币回报率 $R_0$ 是密切相关的。

28.6. 计算方法1#

回顾一下，货币回报率 $R_t$ 存在两个稳态均衡值 $R_\ell < R_u$。

我们按以下步骤进行计算：

从 $t=0$ 开始

选择一个 $R_0 \in [\frac{\gamma_2}{\gamma_1}, R_u]$
计算 $b_0 = \gamma_1 - \gamma_0 R_0^{-1}$

然后对于 $t \geq 1$，通过迭代方程 (28.10) 构造序列 $\{b_t, R_t\}$。

当我们实施方法1时，会发现以下重要结果：

无论从区间 $[\frac{\gamma_2}{\gamma_1}, R_u]$ 中选择哪个 $R_0$ 作为起点，序列 $\{R_t\}$ 总是会收敛到一个取决于初始条件 $R_0$ 的有限”稳态”值 $\bar R$。
这个极限值 $\bar R$ 只有两种可能：$R_\ell$ 或 $R_u$。
对于几乎所有的初始条件 $R_0$，极限值 $\lim_{t \rightarrow +\infty} R_t = R_\ell$。
只有当 $R_0 = R_u$ 时，极限值才会是 $\lim_{t \rightarrow +\infty} R_t = R_u$。

值得注意的是，$1 - R_t$ 可以被解释为政府对货币持有者征收的通货膨胀税率。

我们即将看到，货币回报率存在两个稳态值这一事实表明通货膨胀税率存在一条拉弗曲线，这条曲线描述了政府如何通过通货膨胀为其赤字 $g$ 融资。

Note

拉弗曲线描述了税收收入与税率之间的关系，呈现典型的驼峰形状。这种形状意味着通常存在两个不同的税率能产生相同的税收收入。

这一现象源于两种相互对立的力量：一方面，提高税率会增加单位税基的收入；另一方面，较高的税率往往会导致税基缩小，因为人们会调整自己的行为以减少税负。

def simulate_system(R0, model, num_steps):
    γ1, γ2, g = model.γ1, model.γ2, model.g

    # 初始化数组来存储结果
    b_values = np.empty(num_steps)
    R_values = np.empty(num_steps)

    # 初始值
    b_values[0] = γ1 - γ2/R0
    R_values[0] = 1 / (γ1/γ2 - (1 / γ2) * b_values[0])

    # 按时间迭代
    for t in range(1, num_steps):
        b_t = b_values[t - 1] * R_values[t - 1] + g
        R_values[t] = 1 / (γ1/γ2 - (1/γ2) * b_t)
        b_values[t] = b_t

    return b_values, R_values

让我们写一些代码来绘制初始值 $R_0$ 的多个可能结果。

让我们绘制与不同 $R_0 \in [\frac{\gamma_2}{\gamma_1}, R_u]$ 相关的不同结果。

下方的每一条线代表与不同 $R_0$ 对应的路径。

# 创建 R_0 的网格
R0s = np.linspace(msm.γ2/msm.γ1, msm.R_u, 9)
R0s = np.append(msm.R_l, R0s)
draw_paths(R0s, msm, line_params, num_steps=20)

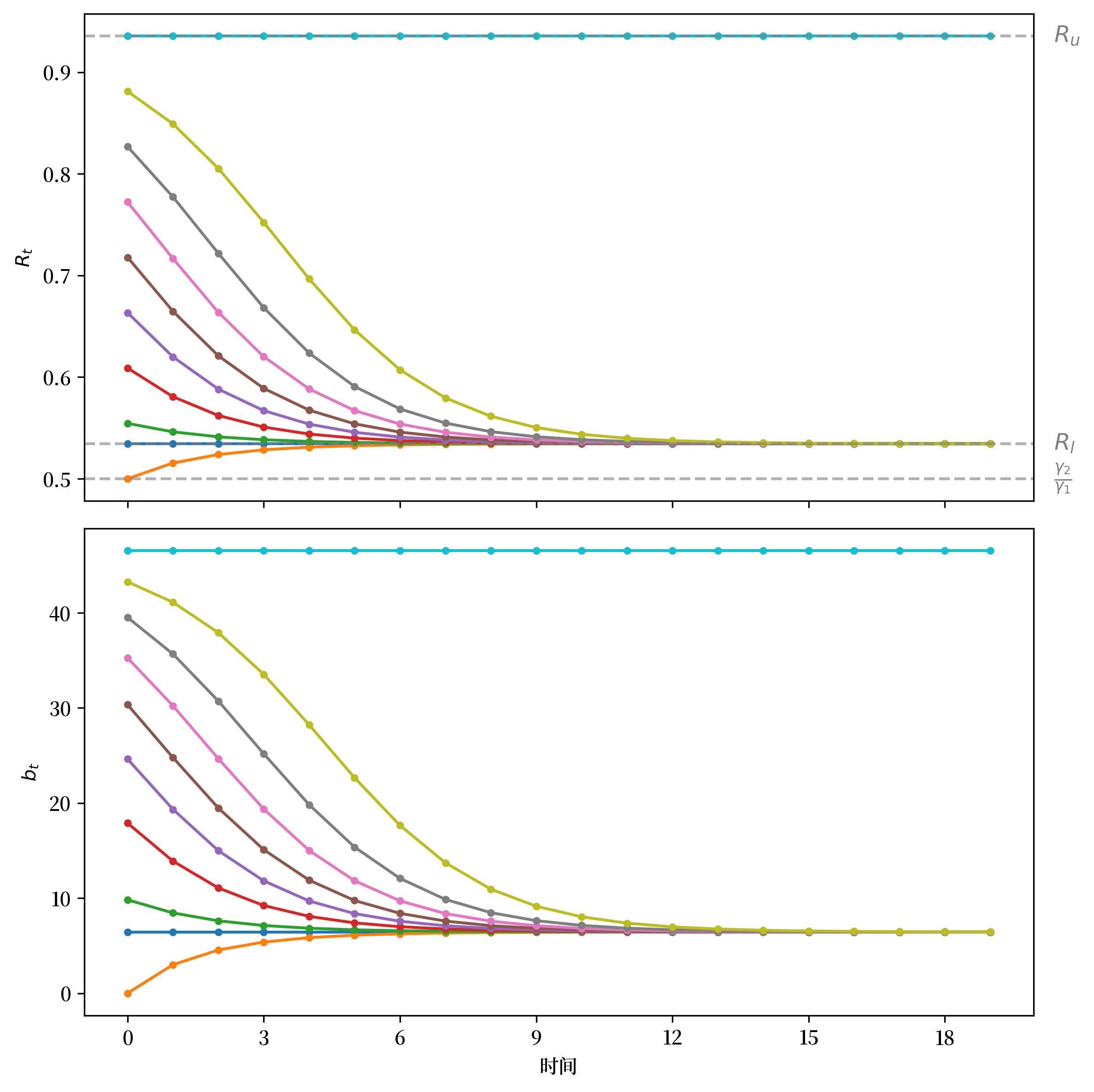
_images/4e34a2bc13cca7a6c9ea581efee655dd5baacb9b4e5e5bb8af9af2ae327d2411.png — Fig. 28.2 从不同初始条件 $R_0$ 出发的 $R_t$（上图）和 $b_t$（下图）的路径#

请关注，序列如何从半开区间 $[R_\ell, R_u)$ 收敛到与 $R_\ell$ 相关的稳态。

28.7. 计算方法 2#

对所有 $t \geq -1$ 令 $m_t = m_t^d $ .

定义

\[ y_t = \begin{bmatrix} m_{t} \cr p_{t} \end{bmatrix} . \]

则平衡条件为 (28.1)、(28.2) 和 (28.3) 如下

(28.13)#\[ \begin{bmatrix} 1 & \gamma_2 \cr 1 & 0 \end{bmatrix} \begin{bmatrix} m_{t+1} \cr p_{t+1} \end{bmatrix} = \begin{bmatrix} 0 & \gamma_1 \cr 1 & g \end{bmatrix} \begin{bmatrix} m_{t} \cr p_{t} \end{bmatrix} \]

或

\[ H_1 y_t = H_2 y_{t-1} \]

其中

\[ \begin{aligned} H_1 & = \begin{bmatrix} 1 & \gamma_2 \cr 1 & 0 \end{bmatrix} \cr H_2 & = \begin{bmatrix} 0 & \gamma_1 \cr 1 & g \end{bmatrix} \end{aligned} \]

H1 = np.array([[1, msm.γ2], 
               [1, 0]])
H2 = np.array([[0, msm.γ1], 
               [1, msm.g]]) 

定义

\[ H = H_1^{-1} H_2 \]

H = np.linalg.solve(H1, H2)
print('H = \n', H)

H = 
 [[ 1.    3.  ]
 [-0.02  1.94]]

将系统 (28.13) 表示为

(28.14)#\[ y_{t+1} = H y_t, \quad t \geq 0 \]

这样，$\{y_t\}_{t=0}$ 可以从以下公式计算

(28.15)#\[ y_t = H^t y_0, t \geq 0 \]

其中

\[ y_0 = \begin{bmatrix} m_{0} \cr p_0 \end{bmatrix} . \]

在这个模型中，我们自然地将 $m_0$ 视为外生给定的初始条件。

然而，数学结构表明 $p_0$ 也需要作为初始条件外部确定，尽管价格水平正是我们希望通过模型内生决定的变量。

（这种情况提醒我们，当数学给我们提示时，我们应该认真思考其含义。）

接下来，让我们基于这一认识继续分析模型的动态特性。

首先，我们计算矩阵 $H$ 的特征向量分解

\[ H = Q \Lambda Q^{-1} \]

其中 $\Lambda$ 是特征值的对角矩阵，$Q$ 的列是对应于这些特征值的特征向量。

结果表明，

\[ \Lambda = \begin{bmatrix} {R_\ell}^{-1} & 0 \cr 0 & {R_u}^{-1} \end{bmatrix} \]

这里的 $R_\ell$ 和 $R_u$ 是我们上面计算出的货币的较低和较高的恒定利率回报。

Λ, Q = np.linalg.eig(H)
print('Λ = ', Λ)
print('Q = ', Q)

Λ =  [1.06887658 1.87112342]
Q =  [[-0.99973655 -0.96033288]
 [-0.02295281 -0.27885616]]

R_l = 1 / Λ[0]
R_u = 1 / Λ[1]

print(f'R_l = {R_l:.4f}')
print(f'R_u = {R_u:.4f}')

R_l = 0.9356
R_u = 0.5344

划分 $Q$ 为

\[\begin{split} Q = \begin{bmatrix} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{bmatrix} \end{split}\]

下面我们将逐步验证以下声明：

**声明：**如果我们设

(28.16)#\[ p_0 = \overline{p}_0 \equiv Q_{21} Q_{11}^{-1} m_{0} , \]

事实证明

\[ \frac{p_{t+1}}{p_t} = {R_u}^{-1}, \quad t \geq 0 \]

然而，如果我们设

\[ p_0 > \overline{p}_0 \]

那么

\[ \lim_{t \rightarrow + \infty} \frac{p_{t+1}}{p_t} = {R_l}^{-1}. \]

让我们逐步验证这些声明。

注意到

\[ H^t = Q \Lambda^t Q^{-1} \]

从而

\[ y_t = Q \Lambda^t Q^{-1} y_0 \]

def iterate_H(y_0, H, num_steps):
    Λ, Q = np.linalg.eig(H)
    Q_inv = np.linalg.inv(Q)
    y = np.stack(
        [Q @ np.diag(Λ**t) @ Q_inv @ y_0 for t in range(num_steps)], 1)
    
    return y

对于几乎所有初始向量 $y_0$，通货膨胀的总率 $\frac{p_{t+1}}{p_t}$ 最终会收敛到较大的特征值 ${R_l}^{-1}$。

避免这种结果的唯一方法是让 $p_0$ 取 (28.16) 中描述的特定值。

为了理解这种情况，我们使用下面的转换

\[ y^*_t = Q^{-1} y_t . \]

$y^*_t$的动态演变明显遵循

(28.17)#\[ y^*_{t+1} = \Lambda^t y^*_t . \]

这个方程所表达的系统的动力可以帮助我们分离出导致通货膨胀趋向较低稳态通货膨胀率 $R_l$ 的逆值的力量。

仔细观察(28.17) 我们可以得出，除非

(28.18)#\[\begin{split}y^*_0 = \begin{bmatrix} y^*_{1,0} \\ 0 \end{bmatrix}\end{split}\]

除非初始条件满足特定要求，否则$y^*_t$的路径，以及由$y_t = Q y^*_t$得到的$m_t$和$p_t$的路径，将随着$t \rightarrow +\infty$最终以$R_l^{-1}$的速率增长。

从方程(28.18)我们可以推断出：存在一个唯一的初始向量$y_0$设置，使得系统的两个组件能够永远以较低的速率${R_u}^{-1}$增长。

要实现这种情况，初始向量$y_0$必须满足以下条件：

\[\begin{split} Q^{-1} y_0 = y^*_0 = \begin{bmatrix} y^*_{1,0} \\ 0 \end{bmatrix} . \end{split}\]

需要注意的是，由于 $y_0 = \begin{bmatrix} m_0 \cr p_0 \end{bmatrix}$，且 $m_0$ 是作为初始条件给定的，因此 $p_0$ 必须进行调整以满足上述方程。

在经济学中，这种情况通常被描述为：$m_0$ 是一个状态变量（不能自由跳跃），而 $p_0$ 是一个跳跃变量（可以在 $t=0$ 时刻自由调整以满足均衡条件）。

总结来说，要使 $y_t$ 的路径不会最终以较高的通胀率 ${R_\ell}^{-1}$ 增长，唯一的方法是选择一个特定的初始向量 $y_0$，使得 $y^*_0$ 的第二个分量为零。

因此，对于初始向量 $y_0 = \begin{bmatrix} m_0 \\ p_0 \end{bmatrix}$，$p_0$ 必须满足

\[ Q^{\{2\}} y_0 = 0 \]

这里 $Q^{\{2\}}$ 表示 $Q^{-1}$ 的第二行，相当于

(28.19)#\[Q^{21} m_0 + Q^{22} p_0 = 0\]

其中 $Q^{ij}$ 表示 $Q^{-1}$ 的 $(i,j)$ 元素。

解这个方程得到 $p_0$，我们发现

(28.20)#\[p_0 = - (Q^{22})^{-1} Q^{21} m_0.\]

28.7.1. 更便捷的公式#

我们可以推导出一个等价但更为简洁的 $p_0$ 表达式 (28.16)，它直接使用矩阵 $Q$ 的元素，而不是 $Q^{-1}$ 的元素。

为了推导这个表达式，我们首先利用矩阵乘法的基本性质。由于 $Q^{-1}Q = I$（单位矩阵），$Q^{-1}$ 的第二行 $(Q^{21}\ Q^{22})$ 与 $Q$ 的第一列相乘必须等于零，即

\[ \begin{bmatrix} Q^{21} & Q^{22} \end{bmatrix} \begin{bmatrix} Q_{11}\cr Q_{21} \end{bmatrix} = 0 \]

这意味着

\[ Q^{21} Q_{11} + Q^{22} Q_{21} = 0. \]

因此，

\[ -(Q^{22})^{-1} Q^{21} = Q_{21} Q^{-1}_{11}. \]

所以我们可以写成

\[p_0 = Q_{21} Q_{11}^{-1} m_0 .\]

这就是我们的公式 (28.16)。

p0_bar = (Q[1, 0]/Q[0, 0]) * msm.M0

print(f'p0_bar = {p0_bar:.4f}')

p0_bar = 2.2959

我们可以验证，这个公式在动态系统中具有稳定性，也就是说

(28.21)#\[p_t = Q_{21} Q^{-1}_{11} m_t.\]

现在让我们从不同的 $p_0$ 值开始，来可视化 $m_t$、$p_t$ 和 $R_t$ 的动态，以验证我们上述的论断。

我们创建一个函数 draw_iterations 来生成图表。

p0s = [p0_bar, 2.34, 2.5, 3, 4, 7, 30, 100_000]

draw_iterations(p0s, msm, line_params, num_steps=20)

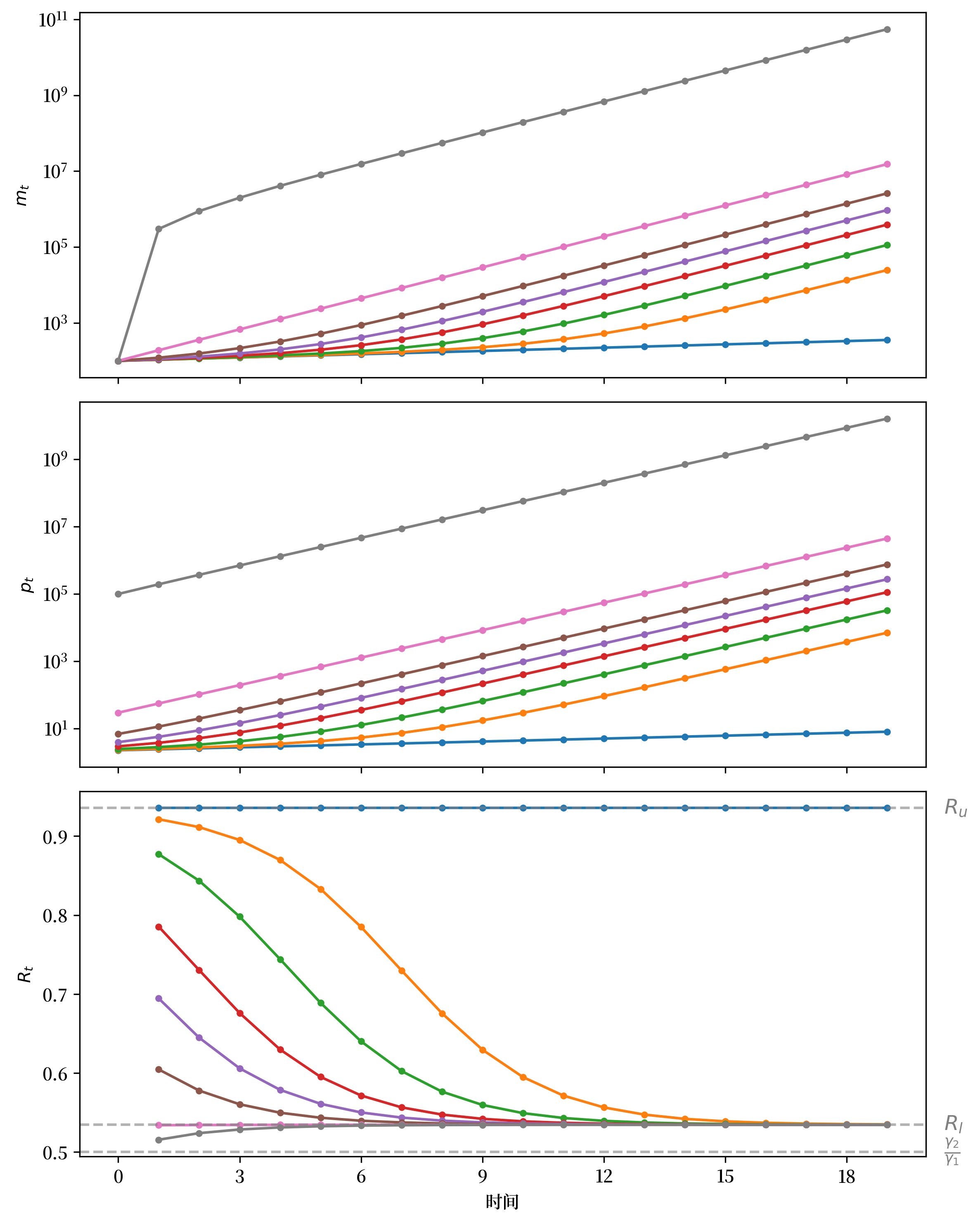
_images/5737d7d791e2fe7ca8510f793e265b0038126d240ff77a9409e282acac2a1d64.png — Fig. 28.3 从不同的初始值 $p_0$ 出发, $m_t$ 的路径（顶部面板，$m$ 使用对数刻度）, $p_t$（中间面板，$m$ 使用对数刻度）, $R_t$（底部面板）#

请注意我们对 $m_t$ 和 $p_t$ 使用了对数刻度。

使用对数刻度使我们能够更容易地通过视觉识别两个不同的常数极限增长率 ${R_u}^{-1}$ 和 ${R_\ell}^{-1}$。

28.8. 特殊的静态结果#

正如本讲座开始时所承诺的，我们遇到了以下宏观经济学概念：

政府通过印制纸币或电子货币征收的通货膨胀税
通货膨胀税率的动态拉弗曲线，该曲线具有两个静态均衡点

观察图 Fig. 28.2 中物价水平回报率的路径和图 Fig. 28.3 中的物价水平路径，我们可以看到几乎所有路径都趋向于图 Fig. 28.1 中拉弗曲线静态状态下显示的较高通货膨胀税率。

因此，我们确实发现了我们早先称为”反常”的动态现象，即在理性预期下，系统收敛到两个可能的静态通货膨胀税率中较高的那个。

这些动态之所以”反常”，不仅是因为它们意味着货币和财政当局选择通过印钞来筹集财政收入，最终征收的通货膨胀税超过了筹集财政支出所需的税收，还因为我们可以从图 Fig. 28.1 中显示的静态拉弗曲线得出以下”违反直觉”的结论：

该图表表明，通过运行更高的政府赤字（即通过印制更多货币来筹集更多资源），实际上可以降低通货膨胀率。

Note

在本讲座通货膨胀税的拉弗曲线中研究的模型的非线性版本中，同样的定性结果仍然适用。

28.9. 均衡选择#

我们的模型在确定价格水平路径方面存在不完整性，因为有多条满足”实际货币余额等于供给”条件的”均衡”路径 $\{m_{t+1}, p_t\}_{t=0}^\infty$。

通过前面介绍的两种计算方法，我们发现这些可能的均衡路径可以通过以下两个参数之一来确定：

计算方法1中的初始回报率 $R_0$
计算方法2中的初始价格水平 $p_0$

要实际应用我们的模型，我们需要从这些可能的均衡路径中选择一条特定路径，从而完成我们的模型。

我们的分析表明：

几乎所有均衡路径最终都会收敛到两个可能的平稳通胀税率中较高的那个
只有一条独特的均衡路径与”减少政府赤字会降低通胀率”这一直觉相符

基于经济直觉和合理性考虑，我们倾向于采纳大多数宏观经济学家的观点，选择那条收敛到较低平稳通胀税率的独特均衡路径。

在后续讲座一些不愉快的货币主义算术中，我们将进一步接受并应用这一观点。

而在讲座拉弗曲线与自适应预期中，我们将探讨 [Bruno and Fischer, 1990] 等学者如何从不同角度支持这一选择。