17. 求解平方根

17.1. 引言

[Russell, 2004] 在第24章讨论早期希腊数学和天文学时，提到了以下这段引人入胜的内容：

早期的毕达哥拉斯学派发现了第一个无理数——2的平方根，并发明了一种巧妙的方法来逼近它的值。

其中最佳方法如下：构造两列数字，分别称为 \(a\) 列和 \(b\) 列，两列均从1开始。在每一步中，新的 \(a\) 值是通过将上一个 \(a\) 值与当前的 \(b\) 值相加得到的；新的 \(b\) 值则是通过将上一个 \(a\) 值的两倍与上一个 \(b\) 值相加得到的。

按此方法得到的前6对数是 \((1,1), (2,3), (5,7), (12,17), (29,41), (70,99)\)。

在每一对中，\(2a^2 - b^2\) 等于1或-1。因此，\(b/a\) 接近于2的平方根，且每进行一步就会更加接近。

读者可以自行验证 \(99/70\) 的平方确实非常接近2。

本讲将深入研究这种古老的平方根计算方法，并运用我们在之前quantecon讲座中学习的矩阵代数知识。

具体而言，本讲可以视为 特征值和特征向量 的延续。

我们将通过一个实例来说明特征向量如何划分出不变子空间，从而帮助构造和分析线性差分方程的解。

当向量 \(x_t\) 从不变子空间开始时，迭代差分方程会使 \(x_{t+j}\) 对所有 \(j \geq 1\) 保持在该子空间中。

这种不变子空间方法在应用经济动力学中有广泛应用，例如在 通过货币资助的政府赤字和价格水平 讲座中就有所体现。

我们将以古希腊数学家用于计算正整数平方根的方法为例，来阐释这一方法。

17.2. 完全平方数与无理数

如果一个整数的平方根也是整数，则称该整数为完全平方数。

完全平方数的序列从以下数值开始：

\[ 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, \ldots \]

而对于非完全平方数的整数，其平方根就是无理数——即无法表示为两个整数的比值，其小数部分是无限不循环的。

古希腊人发明了一种算法来计算整数的平方根，包括那些非完全平方数的整数。

他们的方法主要包含以下步骤：

• 计算特定的整数序列 \(\{y_t\}_{t=0}^\infty\)；

• 求极限值 \(\lim_{t \rightarrow \infty} \left(\frac{y_{t+1}}{y_t}\right) = \bar r\)；

• 从 \(\bar r\) 推导出所需的平方根。

本讲将详细介绍这种方法。

此外，我们还将利用不变子空间理论，探讨该方法的一些变体，这些变体能够更快地趋近于目标平方根。

17.3. 二阶线性差分方程

在讲解古希腊人的平方根计算方法之前，我们先简要介绍二阶线性差分方程。

考虑以下二阶线性差分方程：

(17.1)\[ y_t = a_1 y_{t-1} + a_2 y_{t-2}, \quad t \geq 0 \]

其中 \((y_{-1}, y_{-2})\) 是给定的初始条件。

方程 (17.1) 实际上代表了序列 \(\{y_t\}_{t=0}^\infty\) 的无限多个线性方程。

对于 \(t = 0, 1, 2, \ldots\) 中的每一个 \(t\)，都有一个方程。

我们可以采用 现值 讲座中的方法，将所有这些方程整合为一个矩阵方程，然后通过矩阵求逆来求解。

Note

在这种情况下，矩阵方程涉及可数无穷维方阵与可数无穷维向量的乘法运算。在特定条件下，矩阵乘法和求逆工具可以应用于这类方程。

但我们不会在这里采用这种方法。

相反，我们将寻找一个时不变函数来求解差分方程，即为满足方程(17.1)的序列\(\{y_t\}_{t=0}^\infty\)提供一个公式，使其适用于任意\(t \geq 0\)。

我们要找的是\(y_t\)（当\(t \geq 0\)时）的表达式，将其表示为初始条件\((y_{-1}, y_{-2})\)的函数：

(17.2)\[ y_t = g((y_{-1}, y_{-2});t), \quad t \geq 0. \]

我们称这样的函数\(g\)为差分方程(17.1)的解。

求解的一种方法是采用猜测验证法。

我们首先考虑一对特殊的初始条件，这对初始条件满足：

(17.3)\[ y_{-1} = \delta y_{-2} \]

其中\(\delta\)是待确定的系数。

对于满足(17.3)的初始条件，方程(17.1)可以推导出：

(17.4)\[ y_0 = \left(a_1 + \frac{a_2}{\delta}\right) y_{-1}. \]

我们希望满足：

(17.5)\[ \left(a_1 + \frac{a_2}{\delta}\right) = \delta \]

这可以重写为特征方程：

(17.6)\[ \delta^2 - a_1 \delta - a_2 = 0. \]

运用二次公式求解(17.6)的根，得到：

(17.7)\[ \delta = \frac{ a_1 \pm \sqrt{a_1^2 + 4 a_2}}{2}. \]

对于方程(17.7)给出的两个\(\delta\)值中的任一个，差分方程(17.1)的解为：

(17.8)\[ y_t = \delta^t y_0 , \forall t \geq 0 \]

此处我们定义：

\[ y_0 = \delta y_{-1} . \]

差分方程(17.1)的通解形式为：

(17.9)\[ y_t = \eta_1 \delta_1^t + \eta_2 \delta_2^t \]

其中\(\delta_1, \delta_2\)是特征方程(17.6)的两个解(17.7)，而\(\eta_1, \eta_2\)是两个常数，选择它们以满足

(17.10)\[ \begin{bmatrix} y_{-1} \cr y_{-2} \end{bmatrix} = \begin{bmatrix} \delta_1^{-1} & \delta_2^{-1} \cr \delta_1^{-2} & \delta_2^{-2} \end{bmatrix} \begin{bmatrix} \eta_1 \cr \eta_2 \end{bmatrix} \]

或

(17.11)\[ \begin{bmatrix} \eta_1 \cr \eta_2 \end{bmatrix} = \begin{bmatrix} \delta_1^{-1} & \delta_2^{-1} \cr \delta_1^{-2} & \delta_2^{-2} \end{bmatrix}^{-1} \begin{bmatrix} y_{-1} \cr y_{-2} \end{bmatrix} \]

有时我们可以自由选择初始条件\((y_{-1}, y_{-2})\)，这种情况下，我们利用方程组(17.10)来确定对应的\((\eta_1, \eta_2)\)值。

若选择\((y_{-1}, y_{-2})\)使得\((\eta_1, \eta_2) = (1, 0)\)，则对所有\(t \geq 0\)，有\(y_t = \delta_1^t\)。

若选择\((y_{-1}, y_{-2})\)使得\((\eta_1, \eta_2) = (0, 1)\)，则对所有\(t \geq 0\)，有\(y_t = \delta_2^t\)。

稍后，我们将把前面的计算与矩阵分解联系起来，用一种简洁的方式表示差分方程(17.1)转移矩阵的特征分解。

在介绍完古希腊人如何计算非完全平方正整数的平方根后，我们将回到这个问题。

17.4. 古希腊人的算法

设\(\sigma\)为大于1的正整数。

即\(\sigma \in {\mathcal I} \equiv \{2, 3, \ldots \}\)。

我们的目标是找到一个算法来计算\(\sigma \in {\mathcal I}\)的平方根。

若\(\sqrt{\sigma} \in {\mathcal I}\)，则称\(\sigma\)为完全平方数。

若\(\sqrt{\sigma} \not\in {\mathcal I}\)，则可以证明它是一个无理数。

古希腊人使用递归算法来计算非完全平方数整数的平方根。

该算法对一个二阶线性差分方程的序列\(\{y_t\}_{t=0}^\infty\)进行迭代：

(17.12)\[ y_{t} = 2 y_{t-1} - (1 - \sigma) y_{t-2}, \quad t \geq 0 \]

同时还需要一对整数作为初始条件\(y_{-1}, y_{-2}\)。

首先，我们将应用一些解差分方程的技巧，这些技巧在Samuelson Multiplier-Accelerator中也有使用。

与差分方程(17.12)相关的特征方程为：

(17.13)\[ c(x) \equiv x^2 - 2 x + (1 - \sigma) = 0 \]

（请注意，这是上面方程(17.6)的一个特例。）

对方程(17.13)右侧进行因式分解，得到：

(17.14)\[ c(x)= (x - \lambda_1) (x-\lambda_2) = 0 \]

其中

\[ c(x) = 0 \]

当且仅当\(x = \lambda_1\)或\(x = \lambda_2\)时成立。

这两个特殊的\(x\)值通常被称为\(c(x)\)的零点或根。

通过二次公式求解特征方程(17.13)的根，我们得到：

(17.15)\[ \lambda_1 = 1 + \sqrt{\sigma}, \quad \lambda_2 = 1 - \sqrt{\sigma}. \]

公式(17.15)表明\(\lambda_1\)和\(\lambda_2\)都是\(\sqrt{\sigma}\)的函数，而\(\sqrt{\sigma}\)正是我们和古希腊人想要计算的对象。

古希腊人采用了一种间接方法，巧妙地利用这一性质来计算正整数的平方根。

他们从特定的初始条件\(y_{-1}, y_{-2}\)开始，然后通过迭代差分方程(17.12)来实现这一目标。

差分方程(17.12)的解具有如下形式：

\[ y_t = \lambda_1^t \eta_1 + \lambda_2^t \eta_2 \]

其中\(\eta_1\)和\(\eta_2\)由初始条件\(y_{-1}, y_{-2}\)确定：

(17.16)\[ \begin{aligned} \lambda_1^{-1} \eta_1 + \lambda_2^{-1} \eta_2 & = y_{-1} \cr \lambda_1^{-2} \eta_1 + \lambda_2^{-2} \eta_2 & = y_{-2} \end{aligned} \]

线性方程组 (17.16) 在本讲座的剩余部分将发挥重要作用。

由于 \(\lambda_1 = 1 + \sqrt{\sigma} > 1 > \lambda_2 = 1 - \sqrt{\sigma}\)， 因此对于几乎所有（但不是所有）初始条件，我们有：

\[ \lim_{t \rightarrow \infty} \left(\frac{y_{t+1}}{y_t}\right) = 1 + \sqrt{\sigma}. \]

因此，

\[ \sqrt{\sigma} = \lim_{t \rightarrow \infty} \left(\frac{y_{t+1}}{y_t}\right) - 1. \]

然而，注意如果 \(\eta_1 = 0\)，则：

\[ \lim_{t \rightarrow \infty} \left(\frac{y_{t+1}}{y_t}\right) = 1 - \sqrt{\sigma} \]

所以

\[ \sqrt{\sigma} = 1 - \lim_{t \rightarrow \infty} \left(\frac{y_{t+1}}{y_t}\right). \]

实际上，如果 \(\eta_1 =0\)，那么：

\[ \sqrt{\sigma} = 1 - \left(\frac{y_{t+1}}{y_t}\right) \quad \forall t \geq 0, \]

因此会立即收敛，无需取极限。

对称地，如果 \(\eta_2 =0\)，那么：

\[ \sqrt{\sigma} = \left(\frac{y_{t+1}}{y_t}\right) - 1 \quad \forall t \geq 0 \]

所以同样，会立即收敛，我们不需要计算极限。

线性方程组 (17.16) 有多种使用方式。

• 我们可以将 \(y_{-1}, y_{-2}\) 作为给定的初始条件，并求解 \(\eta_1, \eta_2\)；

• 我们也可以将 \(\eta_1, \eta_2\) 作为给定值，并求解初始条件 \(y_{-1}, y_{-2}\)。

注意我们上面将 \(\eta_1, \eta_2\) 设为 \((0, 1)\) 或 \((1, 0)\) 来举例说明时使用的是第二种方法的。

采用第二种方法，我们构造了 \({\bf R}^2\) 的一个不变子空间。

现在我们讨论的情况是：

对于 \(t \geq 0\) 和方程 (17.12) 的大多数初始条件 \((y_{-1}, y_{-2}) \in {\bf R}^2\)，\(y_t\) 可以表示为 \(y_{t-1}\) 和 \(y_{t-2}\) 的线性组合。

但对于一些特殊的初始条件 \((y_{-1}, y_{-2}) \in {\bf R}^2\)，\(y_t\) 可以仅表示为 \(y_{t-1}\) 的线性函数。

这些特殊的初始条件要求 \(y_{-1}\) 是 \(y_{-2}\) 的线性函数。

之后我们会研究这些特殊的初始条件。

但首先让我们编写一些 Python 代码，从任意的 \((y_{-1}, y_{-2}) \in {\bf R}^2\) 开始，在方程 (17.12) 上迭代。

17.5. 实现

我们现在实现上述算法来计算 \(\sigma\) 的平方根。

在本讲座中，我们使用以下导入：

import numpy as np
import matplotlib.pyplot as plt

import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

def solve_λs(coefs):    
    # 用 numpy.roots来求根
    λs = np.roots(coefs)
    
    # 对根进行排序以保持一致性
    return sorted(λs, reverse=True)

def solve_η(λ_1, λ_2, y_neg1, y_neg2):
    # 对线性系统求解
    A = np.array([
        [1/λ_1, 1/λ_2],
        [1/(λ_1**2), 1/(λ_2**2)]
    ])
    b = np.array((y_neg1, y_neg2))
    ηs = np.linalg.solve(A, b)
    
    return ηs

def solve_sqrt(σ, coefs, y_neg1, y_neg2, t_max=100):
    # 确保 σ 大于 1
    if σ <= 1:
        raise ValueError("σ 必须大于 1")
        
    # 特征根
    λ_1, λ_2 = solve_λs(coefs)
    
    # 求解 η_1 和 η_2
    η_1, η_2 = solve_η(λ_1, λ_2, y_neg1, y_neg2)

    # 计算序列直到 t_max
    t = np.arange(t_max + 1)
    y = (λ_1 ** t) * η_1 + (λ_2 ** t) * η_2
    
    # 计算大 t 时的比率 y_{t+1} / y_t
    sqrt_σ_estimate = (y[-1] / y[-2]) - 1
    
    return sqrt_σ_estimate

# 用 σ = 2 做个例子
σ = 2

# 特征方程
coefs = (1, -2, (1 - σ))

# 求 σ 的平方根
sqrt_σ = solve_sqrt(σ, coefs, y_neg1=2, y_neg2=1)

# 计算误差
dev = abs(sqrt_σ-np.sqrt(σ))
print(f"sqrt({σ}) 大约为 {sqrt_σ:.5f} (误差: {dev:.5f})")

sqrt(2) 大约为 1.41421 (误差: 0.00000)

现在我们考虑 \((\eta_1, \eta_2) = (0, 1)\) 和 \((\eta_1, \eta_2) = (1, 0)\) 的情况

# 计算 λ_1, λ_2
λ_1, λ_2 = solve_λs(coefs)
print(f'特征方程的根为 ({λ_1:.5f}, {λ_2:.5f}))')

特征方程的根为 (2.41421, -0.41421))

# 情况 1: η_1, η_2 = (0, 1)
ηs = (0, 1)

# 计算 y_{t} 和 y_{t-1} 当 t >= 0
y = lambda t, ηs: (λ_1 ** t) * ηs[0] + (λ_2 ** t) * ηs[1]
sqrt_σ = 1 - y(1, ηs) / y(0, ηs)

print(f"对于 η_1, η_2 = (0, 1), sqrt_σ = {sqrt_σ:.5f}")

对于 η_1, η_2 = (0, 1), sqrt_σ = 1.41421

# 情况 2: η_1, η_2 = (1, 0)
ηs = (1, 0)
sqrt_σ = y(1, ηs) / y(0, ηs) - 1

print(f"对于 η_1, η_2 = (1, 0), sqrt_σ = {sqrt_σ:.5f}")

对于 η_1, η_2 = (1, 0), sqrt_σ = 1.41421

我们发现收敛是立即的。接下来，我们将通过以下步骤来呈现上述分析：首先对二阶差分方程 (17.12) 进行向量化处理，然后利用相关状态转移矩阵的特征分解。

17.6. 差分方程的向量化

用一阶矩阵差分方程表示 (17.12)

\[ \begin{bmatrix} y_{t+1} \cr y_{t} \end{bmatrix} = \begin{bmatrix} 2 & - ( 1 - \sigma) \cr 1 & 0 \end{bmatrix} \begin{bmatrix} y_{t} \cr y_{t-1} \end{bmatrix} \]

或

\[ x_{t+1} = M x_t \]

其中

\[ M = \begin{bmatrix} 2 & - (1 - \sigma ) \cr 1 & 0 \end{bmatrix}, \quad x_t= \begin{bmatrix} y_{t} \cr y_{t-1} \end{bmatrix} \]

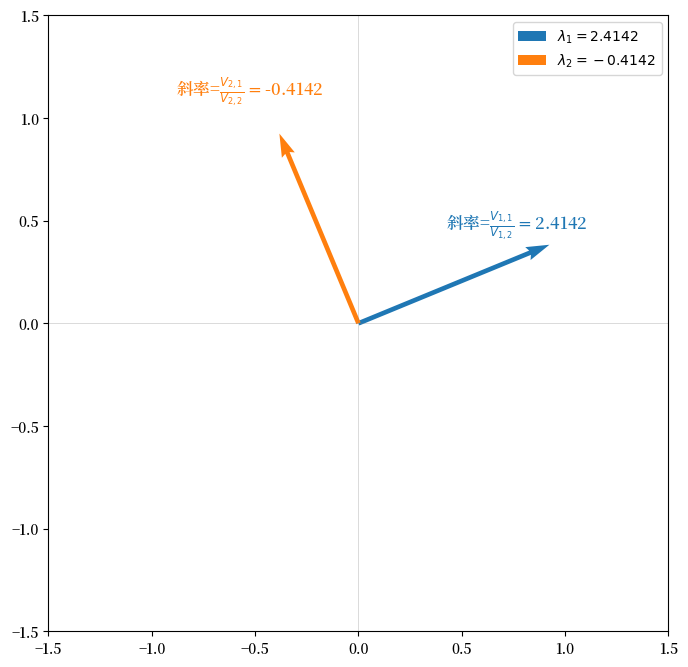
构造 \(M\) 的特征分解：

(17.17)\[ M = V \begin{bmatrix} \lambda_1 & 0 \cr 0 & \lambda_2 \end{bmatrix} V^{-1} \]

其中 \(V\) 的列是对应于特征值 \(\lambda_1\) 和 \(\lambda_2\) 的特征向量。

特征值排序为 \(\lambda_1 > 1 > \lambda_2\)。

将方程 (17.12) 写为

\[ x_{t+1} = V \Lambda V^{-1} x_t \]

现在我们实现上述算法。

首先，我们编写一个迭代 \(M\) 的函数

def iterate_M(x_0, M, num_steps, dtype=np.float64):
    
    # 计算M的特征分解
    Λ, V = np.linalg.eig(M)
    V_inv = np.linalg.inv(V)
    
    # 初始化结果存储数组
    xs = np.zeros((x_0.shape[0], 
                   num_steps + 1))
    
    # 执行迭代
    xs[:, 0] = x_0
    for t in range(num_steps):
        xs[:, t + 1] = M @ xs[:, t]
    
    return xs, Λ, V, V_inv

# 定义状态转移矩阵M
M = np.array([
      [2, -(1 - σ)],
      [1, 0]])

# 定义初始状态向量x_0
x_0 = np.array([2, 2])

# 执行迭代计算
xs, Λ, V, V_inv = iterate_M(x_0, M, num_steps=100)

print(f"特征值：\n{Λ}")
print(f"特征向量：\n{V}")
print(f"特征向量的逆矩阵：\n{V_inv}")

特征值：
[ 2.41421356 -0.41421356]
特征向量：
[[ 0.92387953 -0.38268343]
 [ 0.38268343  0.92387953]]
特征向量的逆矩阵：
[[ 0.92387953  0.38268343]
 [-0.38268343  0.92387953]]

我们将特征值与前面计算的方程(17.13)的根(17.15)进行比较：

roots = solve_λs((1, -2, (1 - σ)))
print(f"特征方程的根：{np.round(roots, 8)}")

特征方程的根：[ 2.41421356 -0.41421356]

这验证了(17.17)的正确性。

所求平方根的信息也蕴含在两个特征向量中。

实际上，每个特征向量定义了\({\mathbb R}^3\)中的一个二维子空间，这些子空间由我们在方程(17.8)中遇到的以下形式的动态特性确定：

(17.18)\[ y_{t} = \lambda_i y_{t-1}, \quad i = 1, 2 \]

在方程(17.18)中，第\(i\)个\(\lambda_i\)等于\(V_{i, 1}/V_{i,2}\)。

下图验证了这一点：

Show source

Hide code cell source

# 绘制特征向量
plt.figure(figsize=(8, 8))

plt.quiver(0, 0, V[0, 0], V[1, 0], angles='xy', scale_units='xy', 
           scale=1, color='C0', label=fr'$\lambda_1={np.round(Λ[0], 4)}$')
plt.quiver(0, 0, V[0, 1], V[1, 1], angles='xy', scale_units='xy', 
           scale=1, color='C1', label=fr'$\lambda_2={np.round(Λ[1], 4)}$')

# 标记斜率
plt.text(V[0, 0]-0.5, V[1, 0]*1.2, 
         r'斜率=$\frac{V_{1,1}}{V_{1,2}}=$'+f'{np.round(V[0, 0] / V[1, 0], 4)}', 
         fontsize=12, color='C0')
plt.text(V[0, 1]-0.5, V[1, 1]*1.2, 
         r'斜率=$\frac{V_{2,1}}{V_{2,2}}=$'+f'{np.round(V[0, 1] / V[1, 1], 4)}', 
         fontsize=12, color='C1')

# 添加标记
plt.axhline(0, color='grey', linewidth=0.5, alpha=0.4)
plt.axvline(0, color='grey', linewidth=0.5, alpha=0.4)
plt.legend()

plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.show()

17.7. 不变子空间方法

前面的计算表明，我们可以利用特征向量\(V\)构造二维不变子空间。

接下来我们将探讨这种可能性。

首先定义变换后的变量：

\[ x_t^* = V^{-1} x_t \]

显然，我们可以从\(x_t^*\)反推得到\(x_t\)：

\[ x_t = V x_t^* \]

下面的符号和方程将在后续分析中发挥重要作用。

令

\[ V = \begin{bmatrix} V_{1,1} & V_{1,2} \cr V_{2,1} & V_{2,2} \end{bmatrix}, \quad V^{-1} = \begin{bmatrix} V^{1,1} & V^{1,2} \cr V^{2,1} & V^{2,2} \end{bmatrix} \]

注意，这源自以下等式：

\[ \begin{bmatrix} V^{1,1} & V^{1,2} \cr V^{2,1} & V^{2,2} \end{bmatrix} \begin{bmatrix} V_{1,1} & V_{1,2} \cr V_{2,1} & V_{2,2} \end{bmatrix} = \begin{bmatrix} 1 & 0 \cr 0 & 1 \end{bmatrix} \]

从中我们可以得到：

\[ V^{2,1} V_{1,1} + V^{2,2} V_{2,1} = 0 \]

以及

\[ V^{1,1}V_{1,2} + V^{1,2} V_{2,2} = 0. \]

这些方程在后续分析中将非常有用。

观察到：

\[ \begin{bmatrix} x_{1,t+1}^* \cr x_{2,t+1}^* \end{bmatrix} = \begin{bmatrix} \lambda_1 & 0 \cr 0 & \lambda_2 \end{bmatrix} \begin{bmatrix} x_{1,t}^* \cr x_{2,t}^* \end{bmatrix} \]

若要使\(\lambda_1\)失效，我们需要设置：

\[ x_{1,0}^* = 0. \]

这可以通过如下设置实现：

(17.19)\[ x_{2,0} = -( V^{1,2})^{-1} V^{1,1} x_{1,0} = V_{2,2} V_{1,2}^{-1} x_{1,0}. \]

若要使\(\lambda_2\)失效，我们需要设置：

\[ x_{2,0}^* = 0 \]

这可以通过如下设置实现：

(17.20)\[ x_{2,0} = -(V^{2,2})^{-1} V^{2,1} x_{1,0} = V_{2,1} V_{1,1}^{-1} x_{1,0}. \]

下面我们将验证公式(17.19)和(17.20)。

为了使\(\lambda_1\)失效，我们使用(17.19)：

xd_1 = np.array((x_0[0], 
                 V[1,1]/V[0,1] * x_0[0]),
                dtype=np.float64)

# 计算 x_{1,0}^*
np.round(V_inv @ xd_1, 8)

array([-0.        , -5.22625186])

我们发现\(x_{1,0}^* = 0\)。

现在我们使用(17.20)使\(\lambda_2\)失效：

xd_2 = np.array((x_0[0], 
                 V[1,0]/V[0,0] * x_0[0]), 
                 dtype=np.float64)

# 计算 x_{2,0}^*
np.round(V_inv @ xd_2, 8)

array([2.1647844, 0.       ])

我们发现\(x_{2,0}^* = 0\)。

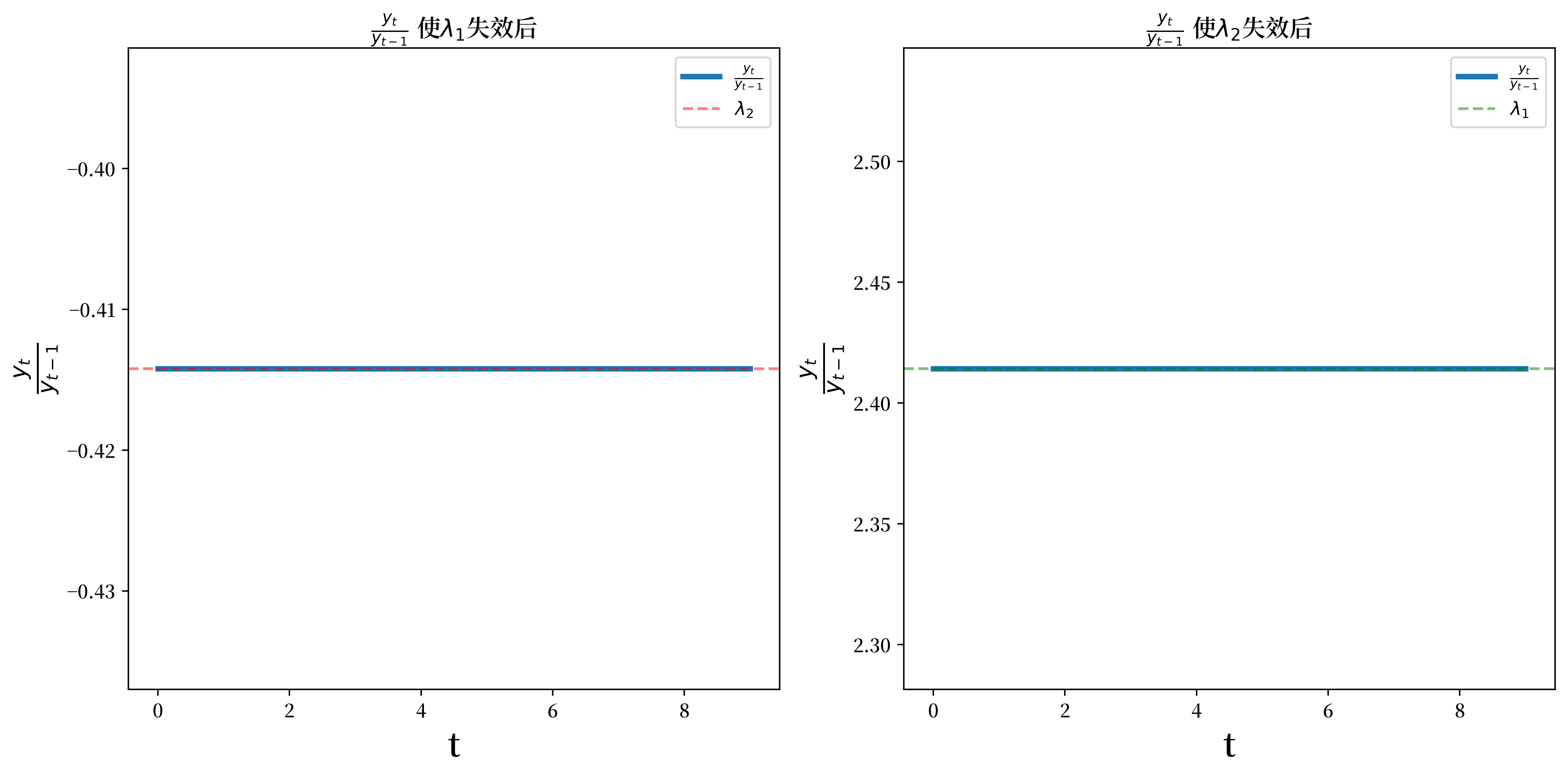
# 模拟使λ1和λ2失效的情况
num_steps = 10
xs_λ1 = iterate_M(xd_1, M, num_steps)[0]
xs_λ2 = iterate_M(xd_2, M, num_steps)[0]

# 计算比值y_t/y_{t-1}
ratios_λ1 = xs_λ1[1, 1:] / xs_λ1[1, :-1]
ratios_λ2 = xs_λ2[1, 1:] / xs_λ2[1, :-1] 

下图展示了两种情况下\(y_t/y_{t-1}\)的比值。

我们观察到，在第一种情况下，比值收敛于\(\lambda_2\)；而在第二种情况下，比值收敛于\(\lambda_1\)。

Show source

Hide code cell source

# 绘制比值y_t/y_{t-1}
fig, axs = plt.subplots(1, 2, figsize=(12, 6), dpi=500)

# 第一子图
axs[0].plot(np.round(ratios_λ1, 6), 
            label=r'$\frac{y_t}{y_{t-1}}$', linewidth=3)
axs[0].axhline(y=Λ[1], color='red', linestyle='--', 
               label=r'$\lambda_2$', alpha=0.5)
axs[0].set_xlabel('t', size=18)
axs[0].set_ylabel(r'$\frac{y_t}{y_{t-1}}$', size=18)
axs[0].set_title(r'$\frac{y_t}{y_{t-1}}$ 使$\lambda_1$失效后', 
                 size=13)
axs[0].legend()

# 第二子图
axs[1].plot(ratios_λ2, label=r'$\frac{y_t}{y_{t-1}}$', 
            linewidth=3)
axs[1].axhline(y=Λ[0], color='green', linestyle='--', 
               label=r'$\lambda_1$', alpha=0.5)
axs[1].set_xlabel('t', size=18)
axs[1].set_ylabel(r'$\frac{y_t}{y_{t-1}}$', size=18)
axs[1].set_title(r'$\frac{y_t}{y_{t-1}}$ 使$\lambda_2$失效后', 
                 size=13)
axs[1].legend()

plt.tight_layout()
plt.show()

17.8. 结束语

本讲为不变子空间方法的众多应用奠定了基础。

所有这些应用都利用了类似的基于特征分解的方程。

在通过货币资助的政府赤字和价格水平和许多其他动态经济理论中，我们将遇到与(17.19)和(17.20)非常相似的方程。

17.9. 练习

Exercise 17.1

请使用矩阵代数来表述伯特兰·罗素（Bertrand Russell）在本讲开始时描述的方法。

1. 定义状态向量\(x_t = \begin{bmatrix} a_t \cr b_t \end{bmatrix}\)。

2. 构建\(x_t\)的一阶向量差分方程，形式为\(x_{t+1} = A x_t\)，并确定矩阵\(A\)。

3. 利用系统\(x_{t+1} = A x_t\)复现伯特兰·罗素所描述的\(a_t\)和\(b_t\)序列。

4. 计算矩阵\(A\)的特征向量和特征值，并与本讲中计算的相应结果进行比较。

Solution to Exercise 17.1

以下是一个解决方案：

根据引用的内容，我们可以表述为：

(17.21)\[\begin{split} \begin{aligned} a_{t+1} &= a_t + b_t \\ b_{t+1} &= 2a_t + b_t \end{aligned} \end{split}\]

其中\(x_0 = \begin{bmatrix} a_0 \cr b_0 \end{bmatrix} = \begin{bmatrix} 1 \cr 1 \end{bmatrix}\)

根据方程(17.21)，矩阵\(A\)可以写为：

\[ A = \begin{bmatrix} 1 & 1 \cr 2 & 1 \end{bmatrix} \]

然后，对于\(t \in \{0, \dots, 5\}\)，有\(x_{t+1} = A x_t\)

# 定义矩阵A
A = np.array([[1, 1],
              [2, 1]])

# 初始向量x_0
x_0 = np.array([1, 1])

# 迭代次数
n = 6

# 生成序列
xs = np.array([x_0])
x_t = x_0
for _ in range(1, n):
    x_t = A @ x_t
    xs = np.vstack([xs, x_t])

# 打印序列
for i, (a_t, b_t) in enumerate(xs):
    print(f"迭代{i}: a_t = {a_t}, b_t = {b_t}")

# 计算A的特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)

print(f'\n特征值:\n{eigenvalues}')
print(f'\n特征向量:\n{eigenvectors}')

迭代0: a_t = 1, b_t = 1
迭代1: a_t = 2, b_t = 3
迭代2: a_t = 5, b_t = 7
迭代3: a_t = 12, b_t = 17
迭代4: a_t = 29, b_t = 41
迭代5: a_t = 70, b_t = 99

特征值:
[ 2.41421356 -0.41421356]

特征向量:
[[ 0.57735027 -0.57735027]
 [ 0.81649658  0.81649658]]