23. 一维动力学#

23.1. 概述#

在经济学中，许多变量依赖于它们的过去值。

例如，我们有理由相信去年的通货膨胀会影响今年的通货膨胀。（比如去年的高通胀会导致人们要求更高的工资作为补偿，导致今年的价格进一步上涨。）

用 $π_{t}$ 表示今年的通货膨胀率， $π_{t - 1}$ 表示去年的通货膨胀率，我们可以用一般形式将这种关系写成：

π_{t} = f (π_{t - 1})

其中 $f$ 是描述变量之间关系的某个函数。

这个方程是一维离散时间动力系统的典型例子。

在本讲中，我们将探讨一维离散时间动力学的基本原理。

（虽然实际经济模型通常包含两个或更多状态变量，但一维框架为我们理解基础理论和掌握核心概念提供了绝佳的起点。）

让我们从一些标准导入开始：

import matplotlib.pyplot as plt
import numpy as np

23.2. 一些定义#

本节将介绍我们要研究的对象和关键概念。

23.2.1. 函数组合#

首先，让我们回顾一下函数组合的概念：

如果

$g$ 是从集合 $A$ 到集合 $B$ 的函数，且
$f$ 是从集合 $B$ 到集合 $C$ 的函数

那么 $f$ 和 $g$ 的组合 $f \circ g$ 定义为

(f \circ g) (x) = f (g (x))

举个简单的例子，如果

$A = B = C = R$ （实数集）
$g (x) = x^{2}$ 且 $f (x) = \sqrt{x}$

那么 $(f \circ g) (x) = \sqrt{x^{2}} = | x |$

当函数映射到自身的集合时，我们可以定义函数的多次组合。如果 $f$ 是从集合 $A$ 到自身的函数，那么 $f^{2}$ 表示 $f$ 与自身的组合。

例如，当 $A = (0, \infty)$ （正实数集）且 $f (x) = \sqrt{x}$ 时，我们有

f^{2} (x) = \sqrt{\sqrt{x}} = x^{1 / 4}

更一般地，对于任意正整数 $n$ ， $f^{n}$ 表示 $f$ 与自身的 $n$ 次组合。

在上面的例子中， $f^{n} (x) = x^{1 / (2^{n})}$ 。

23.2.2. 动态系统#

（离散时间）动态系统由一个集合 $S$ 和一个将 $S$ 映射到自身的函数 $g$ 组成。

动态系统的例子包括：

$S = (0, 1)$ 且 $g (x) = \sqrt{x}$
$S = (0, 1)$ 且 $g (x) = x^{2}$
$S = Z$ （整数集）且 $g (x) = 2 x$

如果 $S = (- 1, 1)$ 且 $g (x) = x + 1$ ，那么 $S$ 和 $g$ 不构成动态系统，因为 $g (1) = 2$ 。

即 $g$ 并不总是将 $S$ 中的点映射回 $S$ 。

研究动态系统的重要性在于它们能帮助我们理解和分析动态过程的基本特性。

给定由集合 $S$ 和函数 $g$ 组成的动态系统，我们可以通过设定

(23.1)#

x_{t + 1} = g (x_{t}) 其中 x_{0} 给定

来创建由 $S$ 中点组成的序列 ${x_{t}}$ 。

这意味着我们选择 $S$ 中的某个数 $x_{0}$ ，然后取

(23.2)#

x_{0}, x_{1} = g (x_{0}), x_{2} = g (x_{1}) = g (g (x_{0})), 等等

这个序列 ${x_{t}}$ 被称为 $x_{0}$ 在 $g$ 下的轨迹。

在这个理论框架下， $S$ 被称为状态空间， $x_{t}$ 被称为状态变量。

回想一下 $g^{n}$ 是 $g$ 与自身的 $n$ 次组合，我们可以更简单地将轨迹写为

x_{t} = g^{t} (x_{0}) 对于 t = 0, 1, 2, \dots

在接下来的所有内容中，我们假设 $S$ 是 $R$ （实数集）的子集。

方程 (23.1) 有时被称为一阶差分方程

一阶意味着只依赖于一个滞后（即，像 $x_{t - 1}$ 这样的更早期的状态不会出现在 (23.1) 中）。

23.2.3. 示例：线性模型#

动态系统的一个典型例子是状态空间 $S = R$ 与映射函数 $g (x) = a x + b$ ，其中 $a, b$ 是常数（有时称为”参数”）。

由此可得线性差分方程

x_{t + 1} = a x_{t} + b 其中 x_{0} 已给定 。

其中 $x_{0}$ 的轨迹是

(23.3)#

x_{0}, a x_{0} + b, a^{2} x_{0} + a b + b, 等等

继续这样下去，并利用我们对几何级数的知识，我们发现，对于任何 $t = 0, 1, 2, \dots$ ，

(23.4)#

x_{t} = a^{t} x_{0} + b \frac{1 - a^{t}}{1 - a}

我们可以对任意非负整数 $t$ 求出 $x_{t}$ 的精确表达式，这让我们能够完全理解系统的动态特性。

值得注意的是，当 $| a | < 1$ 时，根据上面的公式，我们得到

(23.5)#

x_{t} \to \frac{b}{1 - a} 当 t \to \infty

无论起点 $x_{0}$ 为何值。

这是被称为全局稳定性的一个例子，我们将在后面再次讨论这个话题。

23.2.4. 示例：非线性模型#

在上面的线性例子中，我们得到了 $x_{t}$ 关于任意非负整数 $t$ 和 $x_{0}$ 的精确解析式。

这使得动力学分析变得轻而易举。

然而，当模型是非线性时，情况可能会大不相同。

以索洛-斯旺增长模型为例（后续章节将深入分析），其动态规律由以下方程给出

(23.6)#

k_{t + 1} = s A k_{t}^{α} + (1 - δ) k_{t}

这里 $k = K / L$ 表示人均资本存量， $s$ 为储蓄率， $A$ 表示全要素生产率， $α$ 为资本份额， $δ$ 为折旧率。

所有这些参数都是正数，且 $0 < α, δ < 1$ 。

如果你尝试像我们在线性模型中做的那样迭代，你会发现代数运算很快就变得复杂。

分析这个模型的动态需要一种不同的方法（见下文）。

23.3. 稳定性#

考虑这样一个动态系统，其由集合 $S \subset R$ 和将 $S$ 映射到 $S$ 的函数 $g$ 组成。

23.3.1. 稳态#

该系统的稳态是 $S$ 中的一个点 $x^{*}$ ，满足 $x^{*} = g (x^{*})$ 。

换句话说， $x^{*}$ 是函数 $g$ 在 $S$ 中的一个不动点。

例如，对于线性模型 $x_{t + 1} = a x_{t} + b$ ，你可以使用定义来验证：

当 $a \neq 1$ 时， $x^{*} := b / (1 - a)$ 是一个稳态，
如果 $a = 1$ 且 $b = 0$ ，那么每个 $x \in R$ 都是稳态，
如果 $a = 1$ 且 $b \neq 0$ ，那么这个线性模型在 $R$ 中没有稳态。

23.3.2. 全局稳定性#

如果对于所有的 $x_{0} \in S$ ，都有

x_{t} = g^{t} (x_{0}) \to x^{*} 当 t \to \infty

那么动态系统的稳态 $x^{*}$ 被称为全局稳定的。

例如，在线性模型 $x_{t + 1} = a x_{t} + b$ 中，当 $a \neq 1$ 时，稳态 $x^{*}$

如果 $| a | < 1$ ，则是全局稳定的，
否则不是全局稳定的。

以上可以直接从方程 (23.4) 得出。

23.3.3. 局部稳定性#

如果存在一个 $ϵ > 0$ ，使得

| x_{0} - x^{*} | < ϵ ⟹ x_{t} = g^{t} (x_{0}) \to x^{*} 当 t \to \infty

那么动态系统的稳态 $x^{*}$ 被称为局部稳定的。

显然，每个全局稳定的稳态也是局部稳定的。

下面是一个反之不成立的例子。

Example 23.1

考虑 $R$ 上的自映射 $g$ ，定义为 $g (x) = x^{2}$ 。不动点 $1$ 不是稳定的。

例如，对于任何 $x > 1$ ， $g^{t} (x) \to \infty$ 。

然而， $0$ 是局部稳定的，因为当 $- 1 < x < 1$ 时， $g^{t} (x) \to 0$ （当 $t \to \infty$ ）。

由于我们有多个不动点， $0$ 不是全局稳定的。

23.4. 图形分析#

如我们上面所见，分析非线性模型的动态是非常复杂的。

没有一种单一的方法可以处理所有的非线性模型。

然而，对于一维模型，有一种技巧可以提供大量的直观理解。

这是一种基于45度图的图形方法。

让我们看一个例子：索洛-斯旺模型，其动态由(23.6)给出。

我们首先从一些绘图代码开始，你可以在第一次阅读时忽略这些代码。

这段代码的功能是生成45度图和时序图。

Show source Hide code cell source

def subplots():
    "通过原点的自定义子图轴"
    fig, ax = plt.subplots()

    # 通过原点设置坐标轴
    for spine in ['left', 'bottom']:
        ax.spines[spine].set_position('zero')
        ax.spines[spine].set_color('green')
    for spine in ['right', 'top']:
        ax.spines[spine].set_color('none')

    return fig, ax


def plot45(g, xmin, xmax, x0, num_arrows=6, var='x'):

    xgrid = np.linspace(xmin, xmax, 200)

    fig, ax = subplots()
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(xmin, xmax)
    ax.set_xlabel(r'${}_t$'.format(var), fontsize=14)
    ax.set_ylabel(r'${}_{}$'.format(var, str('{t+1}')), fontsize=14)

    hw = (xmax - xmin) * 0.01
    hl = 2 * hw
    arrow_args = dict(fc="k", ec="k", head_width=hw,
            length_includes_head=True, lw=1,
            alpha=0.6, head_length=hl)

    ax.plot(xgrid, g(xgrid), 'b-', lw=2, alpha=0.6, label='g')
    ax.plot(xgrid, xgrid, 'k-', lw=1, alpha=0.7, label='45')

    x = x0
    xticks = [xmin]
    xtick_labels = [xmin]

    for i in range(num_arrows):
        if i == 0:
            ax.arrow(x, 0.0, 0.0, g(x), **arrow_args) # x, y, dx, dy
        else:
            ax.arrow(x, x, 0.0, g(x) - x, **arrow_args)
            ax.plot((x, x), (0, x), 'k', ls='dotted')

        ax.arrow(x, g(x), g(x) - x, 0, **arrow_args)
        xticks.append(x)
        xtick_labels.append(r'${}_{}$'.format(var, str(i)))

        x = g(x)
        xticks.append(x)
        xtick_labels.append(r'${}_{}$'.format(var, str(i+1)))
        ax.plot((x, x), (0, x), 'k', ls='dotted')

    xticks.append(xmax)
    xtick_labels.append(xmax)
    ax.set_xticks(xticks)
    ax.set_yticks(xticks)
    ax.set_xticklabels(xtick_labels)
    ax.set_yticklabels(xtick_labels)

    bbox = (0., 1.04, 1., .104)
    legend_args = {'bbox_to_anchor': bbox, 'loc': 'upper right'}

    ax.legend(ncol=2, frameon=False, **legend_args, fontsize=14)
    plt.show()

def ts_plot(g, xmin, xmax, x0, ts_length=6, var='x'):
    fig, ax = subplots()
    ax.set_ylim(xmin, xmax)
    ax.set_xlabel(r'$t$', fontsize=14)
    ax.set_ylabel(r'${}_t$'.format(var), fontsize=14)
    x = np.empty(ts_length)
    x[0] = x0
    for t in range(ts_length-1):
        x[t+1] = g(x[t])
    ax.plot(range(ts_length),
            x,
            'bo-',
            alpha=0.6,
            lw=2,
            label=r'${}_t$'.format(var))
    ax.legend(loc='best', fontsize=14)
    ax.set_xticks(range(ts_length))
    plt.show()

让我们为索洛-斯旺模型创建一个45度图，使用固定的参数集。以下是对应该模型的更新函数。

def g(k, A = 2, s = 0.3, alpha = 0.3, delta = 0.4):
    return A * s * k**alpha + (1 - delta) * k

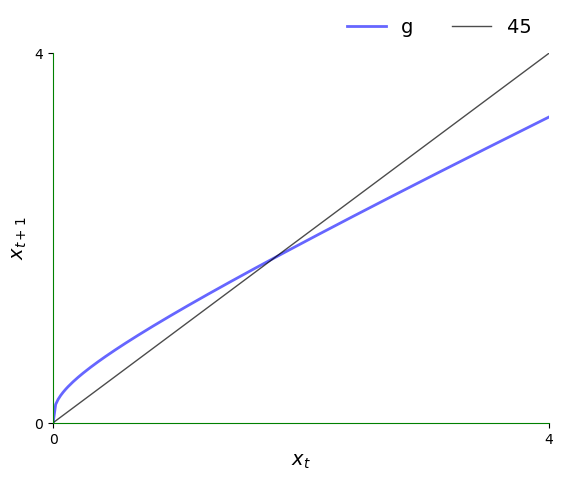
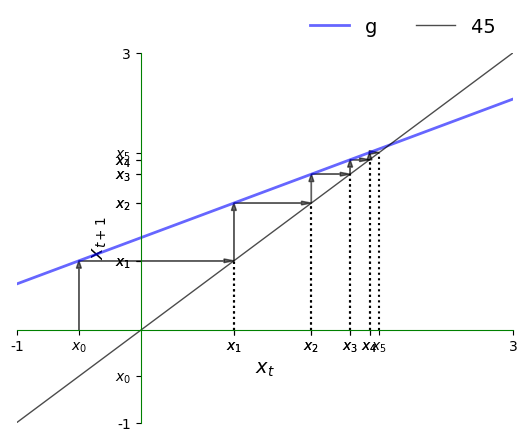
以下是一个45度图。

xmin, xmax = 0, 4  # 适合的绘图区域

plot45(g, xmin, xmax, 0, num_arrows=0)

_images/1b22e04db6d8942db7b7b74e0126e0c76310d3c6cd2e365188831b20f8401350.png

这张图显示了函数 $g$ 和45度线。

可以将 $k_{t}$ 视为横轴上的一个值。

要计算 $k_{t + 1}$ ，我们可以使用 $g$ 的图像来查看其在纵轴上的值。

显然，

如果在这一点上 $g$ 位于45度线之上，那么我们有 $k_{t + 1} > k_{t}$ 。
如果在这一点上 $g$ 位于45度线之下，那么我们有 $k_{t + 1} < k_{t}$ 。
如果在这一点上 $g$ 与45度线相交，那么我们有 $k_{t + 1} = k_{t}$ ，所以 $k_{t}$ 是一个稳态。

对于索洛-斯旺模型，当 $S = R_{+} = [0, \infty)$ 时，有两个稳态。

原点 $k = 0$
唯一的正数，使得 $k = s z k^{α} + (1 - δ) k$ 。

通过一些代数运算，我们可以证明在第二种情况下，其稳态是

k^{*} = {(\frac{s z}{δ})}^{1 / (1 - α)}

23.4.1. 轨迹#

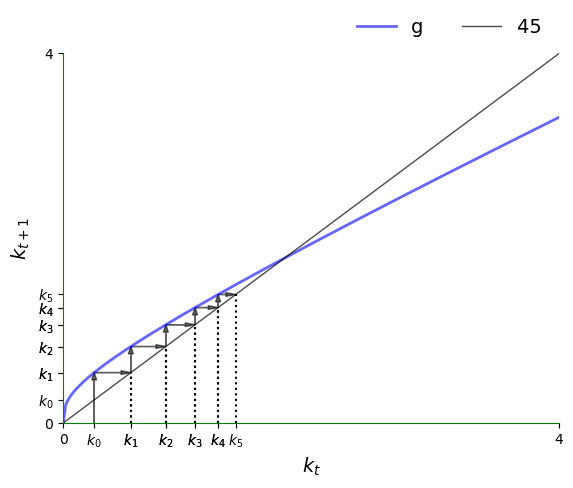
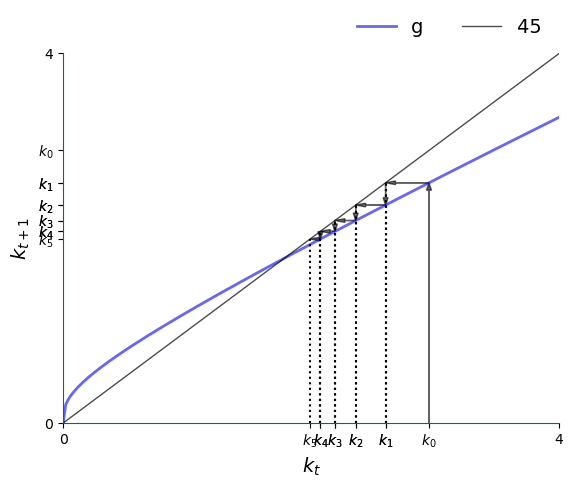
根据前面的讨论，在 $g$ 位于45度线之上的区域，我们知道轨迹是递增的。

下图追踪了这样一个区域内的轨迹，使我们能更清楚地看到这一点。

初始条件是 $k_{0} = 0.25$ 。

k0 = 0.25

plot45(g, xmin, xmax, k0, num_arrows=5, var='k')

_images/db010d4f718a925aa7e9f904c2fe8aaa879f33c54d291649a3cbba303217e635.png

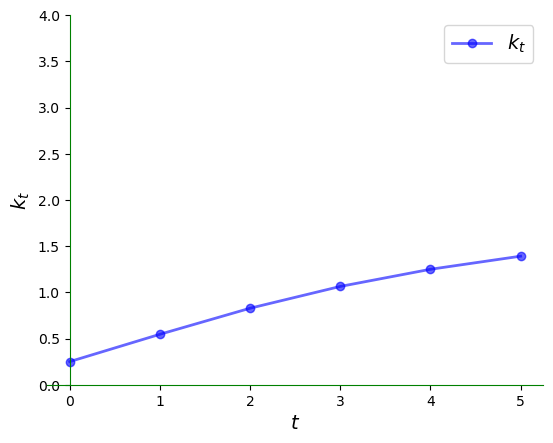
我们可以按照上图所示，绘制人均资本随时间变化的时序图，具体如下：

ts_plot(g, xmin, xmax, k0, var='k')

_images/c9b9199822d7ab92fb684eb7ee9dcbfc45764908741fb6e5116403839372f076.png

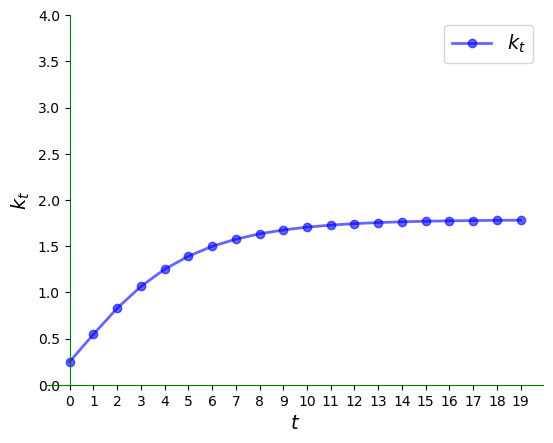
这里是一个稍长期一些的视角：

ts_plot(g, xmin, xmax, k0, ts_length=20, var='k')

_images/14e16a3b15fc7f90dab9694bd42a6a1fbbfd9b968010d3d348e5058bf1890a86.png

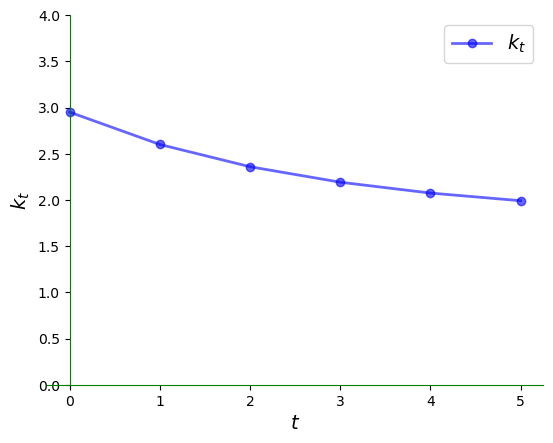
当人均资本存量高于唯一的正稳态值时，我们可以看到它呈下降趋势：

k0 = 2.95

plot45(g, xmin, xmax, k0, num_arrows=5, var='k')

_images/629d30dddd51d46652a4fcd2ea87af943a855ab92861c341edcb290c41132adf.png

这里是一个时间序列：

ts_plot(g, xmin, xmax, k0, var='k')

_images/2c9ec639c951c47d880ec2128bb4f13bc701a14b7c092398c778481a50b1a07d.png

23.4.2. 复杂动态#

尽管索洛-斯旺模型是非线性的，它仍然能生成非常规律的动态。

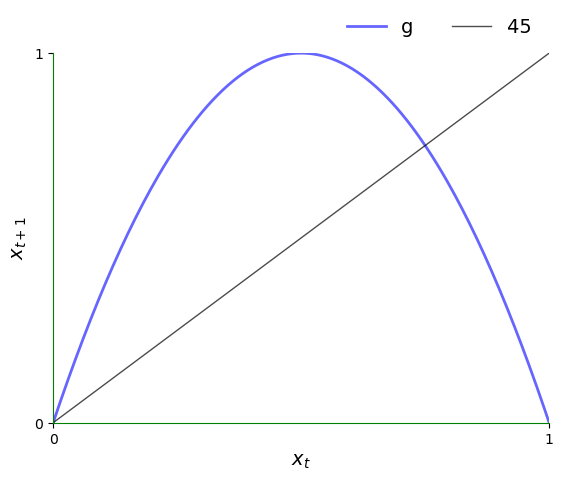
二次映射是一个能生成不规则动态的模型

g (x) = 4 x (1 - x), x \in [0, 1]

让我们来看看45度图。

xmin, xmax = 0, 1
g = lambda x: 4 * x * (1 - x)

x0 = 0.3
plot45(g, xmin, xmax, x0, num_arrows=0)

_images/c5ff7c0276bb777828cbc01d5519c3b81dee173633f74579bb98ea7ae3433dc0.png

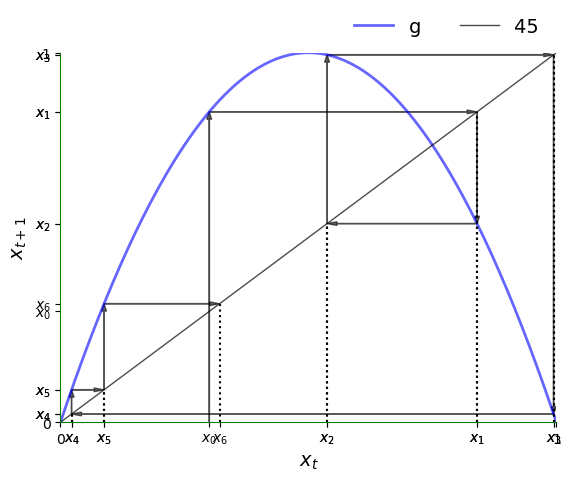
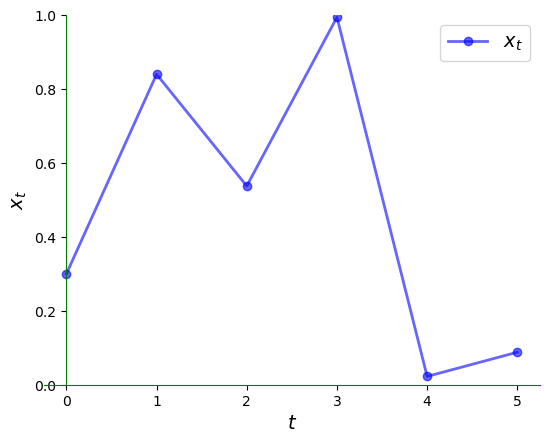
现在让我们来看一个特定的轨迹。

plot45(g, xmin, xmax, x0, num_arrows=6)

_images/7961d872f0961016407a9e95c8f89f6bd34f721a9f6b2873bcd309d4bce8d317.png

注意这个轨迹的不规则性。这种混沌行为是二次映射的典型特征。

这是相应的时序图。

ts_plot(g, xmin, xmax, x0, ts_length=6)

_images/bad45f0dce1be39fffb7fa8135ca88e9f9a95eeb4c953e76843a344eed22b069.png

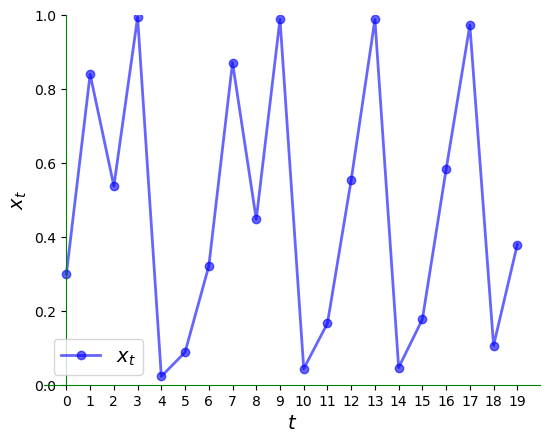
在更长的时间范围内，这种不规则性甚至更加明显：

ts_plot(g, xmin, xmax, x0, ts_length=20)

_images/5d054a31ca9b57bc0c44ba64b2d1006856d40909b60eec2307af137ce2f2bc10.png

23.5. 练习#

Exercise 23.1

再次考虑线性模型 $x_{t + 1} = a x_{t} + b$ ，其中 $a \neq 1$ 。

其唯一的稳态为 $b / (1 - a)$ 。

当 $| a | < 1$ 时，该稳态是全局稳定的。

请通过选择不同的初始条件并绘制相应的图像来验证这一性质。

在 $a \in (- 1, 0)$ 和 $a \in (0, 1)$ 的情况下，你注意到了什么区别？

使用 $a = 0.5$ 和 $a = - 0.5$ 并分别研究轨迹。

在整个过程中设置 $b = 1$ 。

Solution to Exercise 23.1

我们将从 $a = 0.5$ 的情况开始。

让我们设置模型和绘图区域：

a, b = 0.5, 1
xmin, xmax = -1, 3
g = lambda x: a * x + b

现在让我们来绘制轨迹：

x0 = -0.5
plot45(g, xmin, xmax, x0, num_arrows=5)

_images/0a62931bb69d5cd6f8b563a361e8390257a1ce5ace662d24f1a6dce0e047d658.png

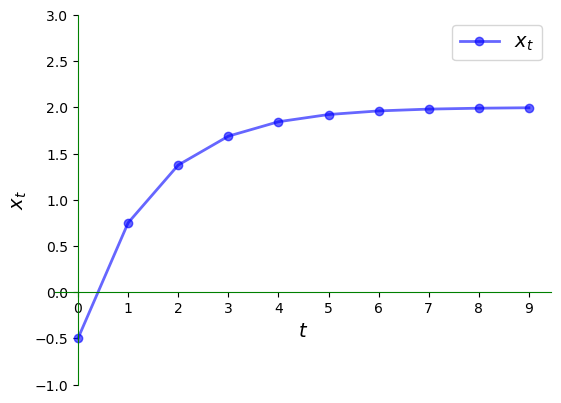
这是相应的时间序列，它收敛于稳态。

ts_plot(g, xmin, xmax, x0, ts_length=10)

_images/a5894d498bd38c37a99ec7fd1da7231fde3c063e04763b270c58b627147916db.png

现在让我们尝试 $a = - 0.5$ 并观察有什么不同。

我们设置模型和绘图区域为：

a, b = -0.5, 1
xmin, xmax = -1, 3
g = lambda x: a * x + b

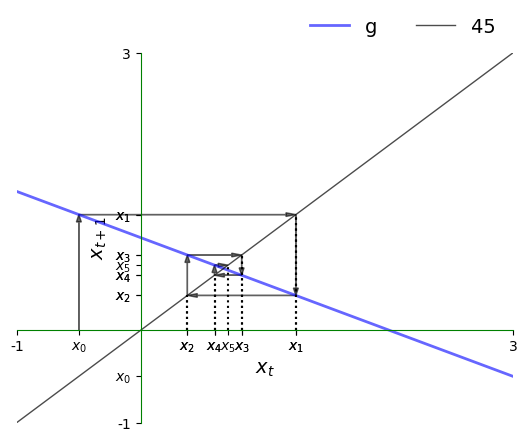
现在让我们来绘制轨迹：

x0 = -0.5
plot45(g, xmin, xmax, x0, num_arrows=5)

_images/d514ceb73f2f313a147955ec9f5b288d027c2e4f6f41c509b693307a39bd0698.png

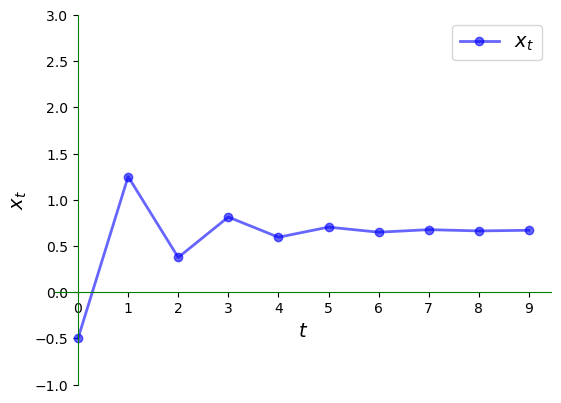
以上是相应的时间序列，它收敛于稳态。

ts_plot(g, xmin, xmax, x0, ts_length=10)

_images/25f0acb334bc8deace12937e4711a541b3947d23ad09f879e103e51d3fad8859.png

我们同样观察到序列收敛到稳态，但收敛方式明显不同。

这次时间序列不是单调收敛，而是在稳态值的上下来回波动，逐渐接近稳态。

这种在接近稳态过程中振幅逐渐减小的波动模式，在动力系统中被称为阻尼振荡。