8. 线性方程和矩阵代数#

8.1. 概述#

经济学和金融学中的许多问题都需要解线性方程。

在本讲座中，我们将讨论线性方程及其应用。

为了说明线性方程的重要性，我们从一个两种商品的供需模型开始。

两种商品的情况非常简单，可以手动计算求解。

但我们经常需要考虑包含多种商品的市场。

在多种商品的情况下，我们面对的是大型线性方程组，有许多方程和未知数。

为了处理这样的系统，我们需要两样知识：

矩阵代数（以及如何使用它的知识）以及
将矩阵代数应用于感兴趣问题的计算机代码。

本讲座涵盖了这些步骤。

我们将使用以下函数库：

import numpy as np
import matplotlib.pyplot as plt

import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

8.2. 两种商品的例子#

在本节中，我们将讨论一个简单的两种商品例子，并通过以下两种方法解决：

纸笔计算
矩阵代数

正如我们将看到的，第二种方法更具普遍性。

8.2.1. 纸笔计算方法#

假设我们有两种相关的商品，比如：

丙烷和乙醇，或
大米和小麦等。

为了简化问题，我们将它们标记为商品0和商品1。

每种商品的需求取决于两种商品的价格：

(8.1)#

\begin{array}{r} \begin{matrix} q_{0}^{d} = 100 - 10 p_{0} - 5 p_{1} \\ q_{1}^{d} = 50 - p_{0} - 10 p_{1} \end{matrix} \end{array}

（我们假设当任一商品的价格上涨时需求会下降，但其他情况也是可能的。）

让我们假设供给由以下方程给出：

(8.2)#

\begin{array}{r} \begin{matrix} q_{0}^{s} = 10 p_{0} + 5 p_{1} \\ q_{1}^{s} = 5 p_{0} + 10 p_{1} \end{matrix} \end{array}

当供给等于需求时（ $q_{0}^{s} = q_{0}^{d}$ 和 $q_{1}^{s} = q_{1}^{d}$ ），市场达到均衡。

这产生了以下线性方程组：

(8.3)#

\begin{array}{r} \begin{matrix} 100 - 10 p_{0} - 5 p_{1} = 10 p_{0} + 5 p_{1} \\ 50 - p_{0} - 10 p_{1} = 5 p_{0} + 10 p_{1} \end{matrix} \end{array}

我们可以用纸笔计算得到：

p_{0} = 4.41 和 p_{1} = 1.18 .

将这些结果代入(8.1)或(8.2)中，可得均衡数量：

q_{0} = 50 和 q_{1} = 33.82 .

8.2.2. 展望未来#

在两种商品的情况下，纸笔计算方法很容易。

但如果有很多种商品呢？

对于这样的问题，我们需要矩阵代数。

在用矩阵代数解决问题之前，让我们先回顾一下向量和矩阵的基础知识，包括理论和计算。

8.3. 向量#

一个长度为 $n$ 的向量就是一个由 $n$ 个数字组成的序列（或数组，或元组），我们将其写作 $x = (x_{1}, \dots, x_{n})$ 或 $x = [\begin{matrix} x_{1}, \dots, x_{n} \end{matrix}]$ 。

我们可以将这些序列横向或纵向写出。

但当我们使用矩阵运算时，我们默认假设向量是列向量。

所有 $n$ 维向量的集合用 $R^{n}$ 表示。

Example 8.1

$R^{2}$ 是平面 — 即所有 $(x_{1}, x_{2})$ 对的集合。
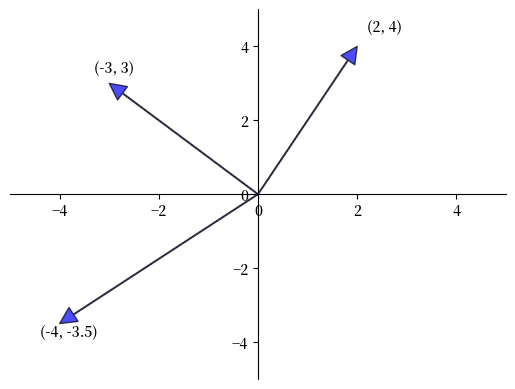
$R^{3}$ 是三维空间 — 即所有 $(x_{1}, x_{2}, x_{3})$ 向量的集合。向量通常在视觉上表示为从原点到某点的箭头。

这里是一个可视化示例。

_images/79c3890876c858c5ec575329cb3865b52c7c6c467e739a12240e6ce334a41202.png

8.3.1. 向量运算#

有时我们需要修改向量。

对向量最常见的两种运算是加法和标量乘法，我们现在来描述这两种运算。

当我们对两个向量进行加法运算时，我们是逐元素相加。

Example 8.2

\begin{array}{r} [\begin{array}{c} 4 \\ - 2 \end{array}] + [\begin{array}{c} 3 \\ 3 \end{array}] = [\begin{array}{c} 4 & + & 3 \\ - 2 & + & 3 \end{array}] = [\begin{array}{c} 7 \\ 1 \end{array}] . \end{array}

一般来说，

\begin{array}{r} x + y = [\begin{array}{c} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{array}] + [\begin{array}{c} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{array}] := [\begin{array}{c} x_{1} + y_{1} \\ x_{2} + y_{2} \\ ⋮ \\ x_{n} + y_{n} \end{array}] . \end{array}

我们可以在 $R^{2}$ 中将向量加法可视化如下。

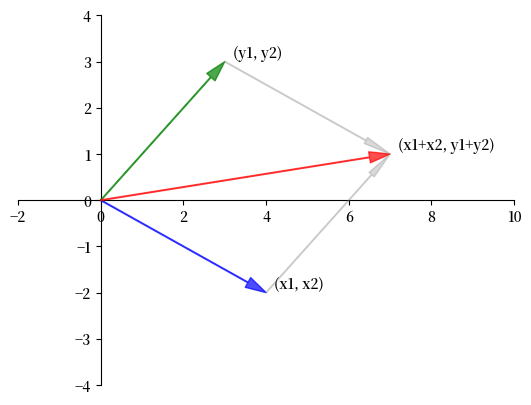
_images/cf94fcba4b4127f164fc27c53e6ac5807eb11dfe3232006ad2a4ff7090580de3.png

标量乘法是一种将向量 $x$ 与一个标量进行元素级别相乘的运算。

Example 8.3

\begin{array}{r} - 2 [\begin{array}{c} 3 \\ - 7 \end{array}] = [\begin{array}{c} - 2 & \times & 3 \\ - 2 & \times & - 7 \end{array}] = [\begin{array}{c} - 6 \\ 14 \end{array}] . \end{array}

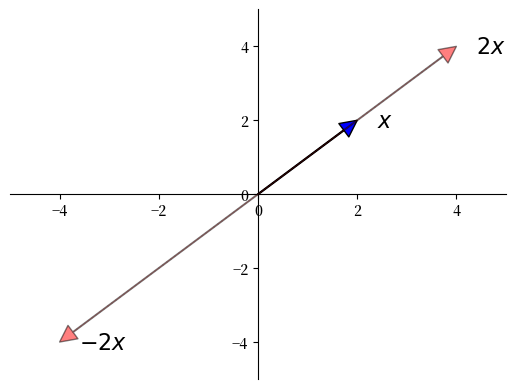
更一般地，它取一个数 $γ$ 和一个向量 $x$ ，得到

\begin{array}{r} γ x := [\begin{array}{c} γ x_{1} \\ γ x_{2} \\ ⋮ \\ γ x_{n} \end{array}] . \end{array}

标量乘法在下图中进行了说明。

_images/7d4f44d624e4e6aa100c364bfb484a900b98a7da18b16f03c807189bce663acd.png

在Python中，向量可以用列表或元组表示，例如 x = [2, 4, 6] 或 x = (2, 4, 6)。

然而，更常见的是用 NumPy数组来表示向量。

使用NumPy数组的一个优点是标量乘法和加法的语法非常自然。

x = np.ones(3)            # 三个元素为一的向量
y = np.array((2, 4, 6))   # 将 (2, 4, 6) 转换为 NumPy 数组
x + y                     # 每个元素相加

array([3., 5., 7.])

4 * x                     # 标量乘法

array([4., 4., 4.])

8.3.2. 内积和范数#

向量 $x, y \in R^{n}$ 的内积定义为

\begin{array}{r} x^{⊤} y = [\begin{array}{c} x_{1} & x_{2} & \dots & x_{n} \end{array}] [\begin{array}{c} y_{1} \\ y_{2} \\ ⋮ \\ y_{n} \end{array}] = x_{1} y_{1} + x_{2} y_{2} + \dots + x_{n} y_{n} := \sum_{i = 1}^{n} x_{i} y_{i} . \end{array}

向量 $x$ 的范数表示其”长度”（即，其与零向量的距离），定义为

‖ x ‖ := \sqrt{x^{⊤} x} := {(\sum_{i = 1}^{n} x_{i}^{2})}^{1 / 2} .

表达式 $‖ x - y ‖$ 可以被理解为 $x$ 和 $y$ 之间的”距离”。

内积和范数可以按以下方式计算

np.sum(x*y)      # x和y的内积

12.0

x @ y            # 另外一种计算内积的办法

12.0

np.sqrt(np.sum(x**2))  # x的范数，方法一

1.7320508075688772

np.linalg.norm(x)      # x的范数，方法二

1.7320508075688772

8.4. 矩阵运算#

当我们讨论线性价格方程组时，我们提到了使用矩阵代数。

矩阵代数类似于算术代数。

让我们回顾一些细节。

8.4.1. 加法和标量乘法#

就像向量一样，我们可以对矩阵进行加法、减法和标量乘法。

标量乘法和加法是向量情况的推广：

Example 8.4

\begin{array}{r} 3 [\begin{array}{c} 2 & - 13 \\ 0 & 5 \end{array}] = [\begin{array}{c} 6 & - 39 \\ 0 & 15 \end{array}] . \end{array}

一般来说，对于任意数 $γ$ 和任意矩阵 $A$ ，

\begin{array}{r} γ A = γ [\begin{array}{c} a_{11} & \dots & a_{1 k} \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} & \dots & a_{n k} \end{array}] := [\begin{array}{c} γ a_{11} & \dots & γ a_{1 k} \\ ⋮ & ⋮ & ⋮ \\ γ a_{n 1} & \dots & γ a_{n k} \end{array}] . \end{array}

Example 8.5

考虑这个矩阵加法的例子，

\begin{array}{r} [\begin{array}{c} 1 & 5 \\ 7 & 3 \end{array}] + [\begin{array}{c} 12 & - 1 \\ 0 & 9 \end{array}] = [\begin{array}{c} 13 & 4 \\ 7 & 12 \end{array}] . \end{array}

一般来说，

\begin{array}{r} A + B = [\begin{array}{c} a_{11} & \dots & a_{1 k} \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} & \dots & a_{n k} \end{array}] + [\begin{array}{c} b_{11} & \dots & b_{1 k} \\ ⋮ & ⋮ & ⋮ \\ b_{n 1} & \dots & b_{n k} \end{array}] := [\begin{array}{c} a_{11} + b_{11} & \dots & a_{1 k} + b_{1 k} \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} + b_{n 1} & \dots & a_{n k} + b_{n k} \end{array}] . \end{array}

在后一种情况下，矩阵必须具有相同的形状才能使定义有意义。

8.4.2. 矩阵乘法#

我们还有一个相乘两个矩阵的约定。

矩阵乘法的规则推广了上面讨论的内积的概念。

如果 $A$ 和 $B$ 是两个矩阵，那么它们的乘积 $A B$ 的形成是通过取 $A$ 的第 $i$ 行和 $B$ 的第 $j$ 列的内积作为其第 $i, j$ 个元素。

如果 $A$ 是 $n \times k$ 的， $B$ 是 $j \times m$ 的，那么要相乘 $A$ 和 $B$ ，我们需要 $k = j$ ，而得到的矩阵 $A B$ 是 $n \times m$ 的。

Example 8.6

这里是一个 $2 \times 2$ 矩阵乘以 $2 \times 1$ 向量的例子。

\begin{array}{r} A x = [\begin{array}{c} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}] [\begin{array}{c} x_{1} \\ x_{2} \end{array}] = [\begin{array}{c} a_{11} x_{1} + a_{12} x_{2} \\ a_{21} x_{1} + a_{22} x_{2} \end{array}] \end{array}

作为一个重要的特殊情况，考虑将 $n \times k$ 矩阵 $A$ 和 $k \times 1$ 列向量 $x$ 相乘。

根据前面的规则，结果是一个 $n \times 1$ 列向量。

(8.4)#

\begin{array}{r} A x = {[\begin{array}{c} a_{11} & a_{12} & \dots & a_{1 k} \\ ⋮ & ⋮ & ⋮ \\ a_{i 1} & a_{i 2} & \dots & a_{i} k \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} & a_{n 2} & \dots & a_{n k} \end{array}]}_{n \times k} {[\begin{array}{c} x_{1} \\ x_{2} \\ ⋮ \\ ⋮ \\ x_{k} \end{array}]}_{k \times 1} := {[\begin{array}{c} a_{11} x_{1} + a_{22} x_{2} + \dots + a_{1 k} x_{k} \\ ⋮ \\ a_{i 1} x_{1} + a_{i 2} x_{2} + \dots + a_{i k} x_{k} \\ ⋮ \\ a_{n 1} x_{1} + a_{n 2} x_{2} + \dots + a_{n k} x_{k} \end{array}]}_{n \times 1} \end{array}

下面展示了两个矩阵的乘法。

\begin{array}{r} A B = [\begin{array}{c} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}] [\begin{array}{c} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array}] := [\begin{array}{c} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \end{array}] \end{array}

有许多教程可以帮助你进一步可视化这个操作，例如

这个教程，或者
维基百科页面上的讨论。

Note

与数字乘积不同， $A B$ 和 $B A$ 通常不相等。

一个重要的特殊情况是单位矩阵，它在主对角线上有 1，其他地方都是 0：

\begin{array}{r} I = [\begin{array}{c} 1 & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & 1 \end{array}] \end{array}

作为练习请验证以下内容：

如果 $A$ 是 $n \times k$ 矩阵， $I$ 是 $k \times k$ 单位矩阵，那么 $A I = A$ ，并且
如果 $I$ 是 $n \times n$ 单位矩阵，那么 $I A = A$ 。

8.4.3. NumPy中的矩阵#

NumPy 数组也被用作矩阵，并且对所有标准矩阵运算都有快速、高效的函数和方法。

你可以通过以下方式从元组的元组（或列表的列表）手动创建它们

A = ((1, 2),
     (3, 4))

type(A)

tuple

A = np.array(A)

type(A)

numpy.ndarray

A.shape

(2, 2)

shape 属性是一个给出行数和列数的元组 — 更多讨论请参见这里。

要获得 A 的转置，使用 A.transpose() 或更简单地使用 A.T。

有许多方便的函数用于创建常见矩阵（零矩阵、单位矩阵等） — 请参见这里。

由于默认情况下操作是按元素执行的，标量乘法和加法具有非常自然的语法。

A = np.identity(3)    # 3 x 3 单位矩阵
B = np.ones((3, 3))   # 3 x 3 元素为一的矩阵
2 * A

array([[2., 0., 0.],
       [0., 2., 0.],
       [0., 0., 2.]])

A + B

array([[2., 1., 1.],
       [1., 2., 1.],
       [1., 1., 2.]])

我们用 @ 来进行矩阵乘法。

Note

其中 A @ B 是矩阵乘法, 但是 A * B是每个元素之间的运算。

8.4.4. 矩阵形式的两种商品模型#

我们现在可以重新审视两种商品模型，并通过矩阵代数数值求解 (8.3) 方程。

这涉及一些额外的步骤，但这种方法广泛适用，我们将在求解包含更多商品时用上。

首先，我们将 (8.1) 重写为

(8.5)#

\begin{array}{r} q^{d} = D p + h where q^{d} = [\begin{array}{c} q_{0}^{d} \\ q_{1}^{d} \end{array}] D = [\begin{array}{c} - 10 & - 5 \\ - 1 & - 10 \end{array}] and h = [\begin{array}{c} 100 \\ 50 \end{array}] . \end{array}

回想一下， $p \in R^{2}$ 是两种商品的价格。

（请检查 $q^{d} = D p + h$ 是否表示与 (8.1) 相同的方程。）

我们将 (8.2) 重写为

(8.6)#

\begin{array}{r} q^{s} = C p where q^{s} = [\begin{array}{c} q_{0}^{s} \\ q_{1}^{s} \end{array}] and C = [\begin{array}{c} 10 & 5 \\ 5 & 10 \end{array}] . \end{array}

现在供给和需求的相等可以表示为 $q^{s} = q^{d}$ ，或

C p = D p + h .

我们可以重新排列这些项得到

(C - D) p = h .

如果所有项都是数字，我们可以求解价格为 $p = h / (C - D)$ 。

矩阵代数允许我们做类似的事情：我们可以使用 $C - D$ 的逆矩阵来求解均衡价格：

(8.7)#

p = (C - D)^{- 1} h .

在我们实施解决方案之前，让我们考虑一个更一般的问题。

8.4.5. 更多商品#

考虑有更多商品的需求系统是很自然的。

例如，即使在能源商品中也有许多不同的商品，包括原油、汽油、煤炭、天然气、乙醇和铀。

这些商品的价格是相关的，所以一起研究它们是有意义的。

对于大型系统，纸笔方法会变得非常耗时。

但幸运的是，上面描述的矩阵方法基本上保持不变。

一般来说，我们可以将需求方程写为 $q^{d} = D p + h$ ，其中

$q^{d}$ 是一个 $n \times 1$ 的向量，表示 $n$ 种不同商品的需求量。
$D$ 是一个 $n \times n$ 的”系数”矩阵。
$h$ 是一个 $n \times 1$ 的常数值向量。

类似地，我们可以将供给方程写为 $q^{s} = C p + e$ ，其中

$q^{s}$ 是一个 $n \times 1$ 的向量，表示相同商品的供给量。
$C$ 是一个 $n \times n$ 的”系数”矩阵。
$e$ 是一个 $n \times 1$ 的常数值向量。

为了找到均衡，我们求解 $D p + h = C p + e$ ，或

(8.8)#

(D - C) p = e - h .

那么，n 种不同商品的价格向量是

p = (D - C)^{- 1} (e - h) .

8.4.6. 一般线性系统#

上述问题的一个更一般版本看起来如下。

(8.9)#

\begin{array}{r} \begin{array}{c} a_{11} x_{1} & + & a_{12} x_{2} & + & \dots & + & a_{1 n} x_{n} & = & b_{1} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ a_{n 1} x_{1} & + & a_{n 2} x_{2} & + & \dots & + & a_{n n} x_{n} & = & b_{n} \end{array} \end{array}

这里的目标是解出”未知数” $x_{1}, \dots, x_{n}$ 。

我们给定系数 $a_{11}, \dots, a_{n n}$ 和常数 $b_{1}, \dots, b_{n}$ 。

注意，我们处理的是未知数数量等于方程数量的情况。

这是我们最有可能找到明确定义解的情况。

（其他情况被称为超定和欠定方程组 — 我们将在后续讲座中讨论这些情况。）

用矩阵形式表示，方程组 (8.9) 变为

(8.10)#

\begin{array}{r} A x = b where A = [\begin{array}{c} a_{11} & \dots & a_{1 n} \\ ⋮ & ⋮ & ⋮ \\ a_{n 1} & \dots & a_{n n} \end{array}] and b = [\begin{array}{c} b_{1} \\ ⋮ \\ b_{n} \end{array}] . \end{array}

例如，(8.8) 具有这种形式，其中

A = D - C, b = e - h 和 x = p .

当考虑诸如 (8.10) 这样的问题时，我们至少需要问以下一些问题：

解是否真的存在？
如果解存在，我们应该如何计算它？

8.5. 解方程组#

再次回顾方程组 (8.9)，我们在此重新写为

(8.11)#

A x = b

我们面临的问题是找到一个向量 $x \in R^{n}$ ，使其解决 (8.11) ，其中 $b$ 和 $A$ 是给定的。

我们可能并不总能找到一个唯一的向量 $x$ 来解决 (8.11) 。

我们在下面举例说明两种这样的情况。

8.5.1. 无解#

考虑由以下给出的方程组：

\begin{array}{r} \begin{aligned} x + 3 y & = 3 \\ 2 x + 6 y & = - 8. \end{aligned} \end{array}

可以手动验证这个系统没有可能的解。

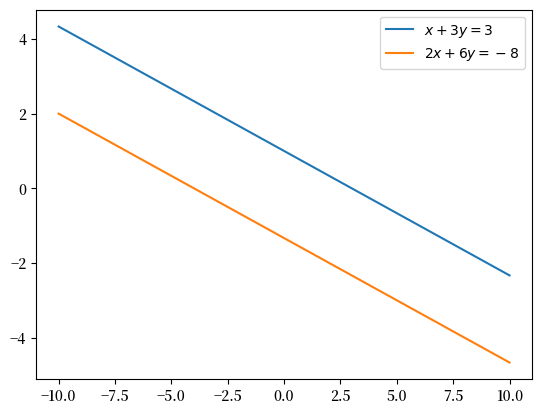
为了说明为什么会出现这种情况，让我们绘制这两条直线。

fig, ax = plt.subplots()
x = np.linspace(-10, 10)
plt.plot(x, (3-x)/3, label=f'$x + 3y = 3$')
plt.plot(x, (-8-2*x)/6, label=f'$2x + 6y = -8$')
plt.legend()
plt.show()

_images/171bc7305cc4c31ffd7a3988e6e4bec781432a59064f6ea34adc6539fb227408.png

显然，这些是平行线，因此我们永远无法找到一个点 $x \in R^{2}$ 使得这些线相交。

因此，这个系统没有可能的解。

我们可以将这个系统用矩阵形式重写为

(8.12)#

\begin{array}{r} A x = b where A = [\begin{array}{c} 1 & 3 \\ 2 & 6 \end{array}] and b = [\begin{array}{c} 3 \\ - 8 \end{array}] . \end{array}

可以注意到，矩阵 $A$ 的第 $2$ 行 $(2, 6)$ 只是第 $1$ 行 $(1, 3)$ 的标量倍数。

在这种情况下，矩阵 $A$ 的行被称为线性相关的。

Note

读者可以在这里找到关于线性相关和线性无关的详细解释。

但在接下来的内容中不需要这些细节。

8.5.2. 多解#

现在考虑，

\begin{array}{r} \begin{aligned} x - 2 y & = - 4 \\ - 2 x + 4 y & = 8. \end{aligned} \end{array}

任何满足 $x = 2 y - 4$ 的向量 $v = (x, y)$ 都将解决上述系统。

由于我们可以找到无限多个这样的向量，这个系统有无穷多个解。

这是因为对应矩阵的行

(8.13)#

\begin{array}{r} A = [\begin{array}{c} 1 & - 2 \\ - 2 & 4 \end{array}] . \end{array}

是线性相关的 — 你能看出为什么吗？

我们现在对 (8.11) 中的 $A$ 施加条件，以排除这些问题。

8.5.3. 非奇异矩阵#

对于每个方阵，我们都可以指定一个唯一的数，称为行列式。

对于 $2 \times 2$ 矩阵，行列式由以下公式给出：

\begin{array}{r} [\begin{array}{c} a & b \\ c & d \end{array}] = a d - b c . \end{array}

如果 $A$ 的行列式不为零，我们就说 $A$ 是非奇异的。

当且仅当 $A$ 的行和列是线性无关的，方阵 $A$ 才是非奇异的。

关于矩阵逆的更详细解释可以在这里找到。

你可以自己检查 (8.12) 和 (8.13) 中具有线性相关行的矩阵是奇异矩阵。

这为我们提供了一个有用的单数值标准，用来判断一个方阵是否可逆。

特别地，方阵 $A$ 具有非零行列式，当且仅当它具有逆矩阵 $A^{- 1}$ ，满足 $A A^{- 1} = A^{- 1} A = I$ 。

因此，如果我们用 $A^{- 1}$ 左乘 $A x = b$ 的两边，我们得到

(8.14)#

x = A^{- 1} b .

这是对 $A x = b$ 的解答 — 这就是我们要寻找的解。

8.5.4. 使用NumPy求解线性方程#

根据上述例子中，我们得到了矩阵方程：

p = (C - D)^{- 1} h .

其中 $C$ 、 $D$ 和 $h$ 由 (8.5) 和 (8.6) 给出。

这个方程类似于 (8.14)，其中 $A = (C - D)^{- 1}$ ， $b = h$ ，且 $x = p$ 。

我们现在可以使用NumPy的linalg子模块求解均衡价格。

所有这些程序都是经过时间考验和高度优化的FORTRAN代码的Python前端。

C = ((10, 5),      # 矩阵 C
     (5, 10))

现在我们把它录入到NumPy数组中。

C = np.array(C)

D = ((-10, -5),     # 矩阵 D
     (-1, -10))
D = np.array(D)

h = np.array((100, 50))   # 向量 h
h.shape = 2,1             # 将h转换为列向量

from numpy.linalg import det, inv
A = C - D
#检查A是否为奇异矩阵（行列式是否为零），是否可逆
det(A)

340.0000000000001

A_inv = inv(A)  #计算逆矩阵
A_inv

array([[ 0.05882353, -0.02941176],
       [-0.01764706,  0.05882353]])

p = A_inv @ h  #均衡价格
p

array([[4.41176471],
       [1.17647059]])

q = C @ p  # 均衡数量
q

array([[50.        ],
       [33.82352941]])

注意，我们得到的解与纸笔计算的情况相同。

我们还可以使用 solve(A, h) 来求解 $p$ ，如下所示。

from numpy.linalg import solve
p = solve(A, h)  # 均衡价格
p

array([[4.41176471],
       [1.17647059]])

q = C @ p  # 均衡数量
q

array([[50.        ],
       [33.82352941]])

观察我们如何通过 inv(A) @ y 或使用 solve(A, y) 来求解 $x = A^{- 1} y$ 。

后一种方法使用了一种不同的算法，在数值上更加稳定，因此应该是默认选项。

8.6. 练习#

Exercise 8.1

让我们考虑一个有3种商品的市场 - 商品0、商品1和商品2。

每种商品的需求取决于其他两种商品的价格，由以下公式给出：

\begin{array}{r} \begin{aligned} q_{0}^{d} & = 90 - 15 p_{0} + 5 p_{1} + 5 p_{2} \\ q_{1}^{d} & = 60 + 5 p_{0} - 10 p_{1} + 10 p_{2} \\ q_{2}^{d} & = 50 + 5 p_{0} + 5 p_{1} - 5 p_{2} \end{aligned} \end{array}

（这里，当自身价格上涨时需求下降，但当其他商品价格上涨时需求增加。）

每种商品的供给由以下公式给出：

\begin{array}{r} \begin{aligned} q_{0}^{s} & = - 10 + 20 p_{0} \\ q_{1}^{s} & = - 15 + 15 p_{1} \\ q_{2}^{s} & = - 5 + 10 p_{2} \end{aligned} \end{array}

当供给等于需求时，市场达到均衡，即 $q_{0}^{d} = q_{0}^{s}$ ， $q_{1}^{d} = q_{1}^{s}$ 和 $q_{2}^{d} = q_{2}^{s}$ 。

将市场均衡条件设置为线性方程组。
使用矩阵代数求解均衡价格。分别使用 numpy.linalg.solve 和 inv(A) 方法来做这个。比较这两种解法。

Solution to Exercise 8.1

生成的系统将是：

\begin{array}{r} \begin{matrix} 35 p_{0} - 5 p_{1} - 5 p_{2} = 100 \\ - 5 p_{0} + 25 p_{1} - 10 p_{2} = 75 \\ - 5 p_{0} - 5 p_{1} + 15 p_{2} = 55 \end{matrix} \end{array}

用矩阵形式，我们将其表示为：

\begin{array}{r} A p = b 其中 A = [\begin{array}{c} 35 & - 5 & - 5 \\ - 5 & 25 & - 10 \\ - 5 & - 5 & 15 \end{array}], p = [\begin{array}{c} p_{0} \\ p_{1} \\ p_{2} \end{array}] 且 b = [\begin{array}{c} 100 \\ 75 \\ 55 \end{array}] \end{array}

import numpy as np
from numpy.linalg import det

A = np.array([[35, -5, -5],  # 矩阵 A
              [-5, 25, -10],
              [-5, -5, 15]])

b = np.array((100, 75, 55))  # 列向量 b
b.shape = (3, 1)

det(A)  # 检查A是否为奇异矩阵

9999.99999999999

# 使用inverse
from numpy.linalg import det

A_inv = inv(A)

p = A_inv @ b
p

array([[4.9625],
       [7.0625],
       [7.675 ]])

# 使用 numpy.linalg.solve
from numpy.linalg import solve
p = solve(A, b)
p

array([[4.9625],
       [7.0625],
       [7.675 ]])

答案为：

p_{0} = 4.6925, p_{1} = 7.0625 and p_{2} = 7.675

Exercise 8.2

在讲座的早些时候，我们讨论了 $A x = b$ 这个方程组没有解的情况。

在这种情况下， $A x = b$ 被称为不相容方程组。

面对不相容系统时，我们尝试找到最佳的”近似”解。

有多种方法可以做到这一点，其中一种是最小二乘法。

假设我们有一个不相容系统

(8.15)#

A x = b

其中 $A$ 是一个 $m \times n$ 矩阵， $b$ 是一个 $m \times 1$ 列向量。

对于(8.15)，最小二乘解是一个 $n \times 1$ 列向量 $\hat{x}$ ，使得对于所有其他向量 $x \in R^{n}$ ， $A \hat{x}$ 到 $b$ 的距离小于 $A x$ 到 $b$ 的距离。

即，

‖ A \hat{x} - b ‖ \leq ‖ A x - b ‖

可以证明，对于方程组 $A x = b$ ，最小二乘解 $\hat{x}$ 是

(8.16)#

\hat{x} = (A^{T} A)^{- 1} A^{T} b

现在考虑一种商品的线性需求曲线的一般方程：

p = m - n q

其中 $p$ 是商品的价格， $q$ 是需求量。

假设我们正试图估计 $m$ 和 $n$ 的值。

我们通过重复观察价格和数量（例如，每个月）来做到这一点，然后选择 $m$ 和 $n$ 来拟合 $p$ 和 $q$ 之间的关系。

我们有以下观察结果：

价格	需求量
1	9
3	7
8	3

要求需求曲线 $p = m - n q$ 通过所有这些点，得到以下三个方程：

\begin{array}{r} \begin{matrix} 1 = m - 9 n \\ 3 = m - 7 n \\ 8 = m - 3 n \end{matrix} \end{array}

因此，我们得到一个方程组 $A x = b$ ，其中 $A = [\begin{matrix} 1 & - 9 \\ 1 & - 7 \\ 1 & - 3 \end{matrix}]$ ， $x = [\begin{matrix} m \\ n \end{matrix}]$ ， $b = [\begin{matrix} 1 \\ 3 \\ 8 \end{matrix}]$ 。可以验证这个系统没有解。

（问题在于我们有三个方程但只有两个未知数。）

因此，我们将尝试找到 $x$ 的最佳近似解。

使用(8.16)和矩阵代数找到最小二乘解 $\hat{x}$ 。
使用numpy.linalg.lstsq找到最小二乘解，并比较结果。

Solution to Exercise 8.2

import numpy as np
from numpy.linalg import inv

# 运用线性代数
A = np.array([[1, -9],  # 矩阵 A
              [1, -7],
              [1, -3]])

A_T = np.transpose(A)  # 矩阵A的转置

b = np.array((1, 3, 8))  # 列向量 b
b.shape = (3, 1)

x = inv(A_T @ A) @ A_T @ b
x

array([[11.46428571],
       [ 1.17857143]])

# 使用 numpy.linalg.lstsq
x, res, _, _ = np.linalg.lstsq(A, b, rcond=None)

x̂ = [[11.46428571]
 [ 1.17857143]]
‖Ax̂ - b‖² = 0.07142857142857066

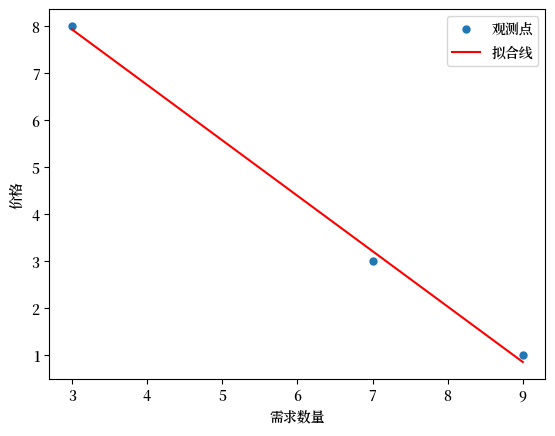
这是一个可视化图，展示了最小二乘法如何近似一组点之间连线的方程。

我们也可以将此描述为在一组点之间”拟合”一条直线。

fig, ax = plt.subplots()
p = np.array((1, 3, 8))
q = np.array((9, 7, 3))

a, b = x

ax.plot(q, p, 'o', label='观测点', markersize=5)
ax.plot(q, a - b*q, 'r', label='拟合线')
plt.xlabel('需求数量')
plt.ylabel('价格')
plt.legend()
plt.show()

_images/611445b5d14e5eefea327d75e4ef3c3e5ad9ffd79e1d4214c916b5599d2bb428.png

8.6.1. 延伸阅读#

numpy.linalg 子模块的文档可以阅读这里。

如果对更高级的线性代数知识感兴趣可以继续阅读这里。