26. 世代交叠模型

在这节课中，我们将学习著名的世代交叠（OLG）模型。政策制定者和研究人员使用这个模型来研究：

• 财政政策

• 货币政策

• 长期增长

以及许多其他主题。

世代交叠模型的第一个严谨版本由保罗·萨缪尔森(Paul Samuelson)在1958年提出[Samuelson, 1958]，此后成为经济学中研究代际问题的基础框架。

在这一讲中，我们将深入探讨世代交叠模型的一个简单版本，帮助大家理解其核心机制和应用。

26.1. 概述

OLG模型的动态与索洛-斯旺增长模型非常相似。

与索洛-斯旺模型相比，OLG模型的一个关键区别是储蓄决策是内生的。

这一特征为什么重要呢？考虑我们想要分析一项新税收政策对经济增长的影响。

在索洛-斯旺模型中，我们可以引入税收并观察稳态如何变化。但这种方法忽略了一个重要现实：税收政策会改变家庭的储蓄和消费行为。

当家庭面对新的税率时，他们会调整自己的经济决策，这些调整可能会显著影响模型的预测结果。

因此，为了获得更准确的预测，我们需要明确建模个人的决策过程。在OLG模型中，家庭会根据他们所处的经济环境（包括技术水平、税收政策和市场价格等）来优化他们的储蓄和消费选择。

OLG模型正是为解决这类问题而设计的。

在接下来的内容中，我们将探讨OLG模型的基本版本，详细说明家庭如何做出决策，并分析这些决策如何影响经济的长期增长。

首先，让我们导入需要的库。

import numpy as np
from scipy import optimize
from collections import namedtuple
import matplotlib.pyplot as plt

import matplotlib as mpl
FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

26.2. 环境

我们假设时间是离散的，因此 \(t=0, 1, \ldots\)。

在时间 \(t\) 出生的个体存活两个时期，\(t\) 和 \(t + 1\)。

我们称一个个体

• 在生命的第一个时期为”年轻人”

• 在生命的第二个时期为”老年人”。

年轻人工作，提供劳动并赚取劳动收入。

他们还决定存多少钱。

老年人不工作，所以所有收入都是金融收入。

他们的金融收入来自工资收入的储蓄利息， 这些储蓄随后与 \(t+1\) 时期新的年轻一代的劳动相结合。

在均衡状态下，工资和利率由市场供求关系决定。

为了使代数计算稍微简单一些，我们假设人口规模恒定。

我们将每个时期的恒定人口规模标准化为1。

我们还假设每个个体提供一个”单位”的劳动时间，因此总劳动供给为1。

26.3. 资本供给

现在让我们从单个家庭的角度开始分析模型。

26.3.1. 消费者问题

假设在时间 \(t\) 出生的个体的效用函数形式为

(26.1)\[ U_t = u(c_t) + \beta u(c_{t+1})\]

其中

• \(u: \mathbb R_+ \to \mathbb R\) 是”瞬时”效用函数（或”流”效用函数）

• \(\beta \in (0, 1)\) 是时间偏好的贴现因子

• \(c_t\) 表示 \(t\) 期出生的个体在年轻时期（即 \(t\) 期）的消费

• \(c_{t+1}\) 表示该个体在老年时期（即 \(t+1\) 期）的消费

我们假设效用函数 \(u\) 是严格递增的。

个体的储蓄决策来自于解决以下效用最大化问题

(26.2)\[ \max_{c_t, c_{t+1}} \, \left \{ u(c_t) + \beta u(c_{t+1}) \right \} \]

受制于

\[ c_t + s_t \le w_t \quad \text{and} \quad c_{t+1} \le R_{t+1} s_t \]

这里

• \(s_t\) 是出生于时间 \(t\) 的个人的储蓄

• \(w_t\) 是时间 \(t\) 的工资率

• \(R_{t+1}\) 是在时间 \(t\) 投资的储蓄在时间 \(t+1\) 支付的总利率

由于效用函数 \(u\) 是严格递增的，消费者会完全用尽预算约束，使两个约束等式成立。

将第一个约束改写为 \(s_t = w_t - c_t\)，并代入第二个约束，我们得到 \(c_{t+1} = R_{t+1}(w_t - c_t)\)。

为了求解最大化问题，我们将 \(c_{t+1} = R_{t+1}(w_t - c_t)\) 代入目标函数，然后对 \(c_t\) 求导并设为零。

这给出了OLG模型的欧拉方程，它刻画了消费者在不同时期之间如何优化分配消费：

(26.3)\[ u'(c_t) = \beta R_{t+1} u'( R_{t+1} (w_t - c_t))\]

从第一个约束我们得到 \(c_t = w_t - s_t\)，所以欧拉方程 也可以表示为

(26.4)\[ u'(w_t - s_t) = \beta R_{t+1} u'( R_{t+1} s_t)\]

假设对于每个 \(w_t\) 和 \(R_{t+1}\)，恰好有一个 \(s_t\) 可以满足 (26.4)。

那么储蓄可以被写成 \(w_t\) 和 \(R_{t+1}\) 的固定函数。

我们将其表示为

(26.5)\[ s_t = s(w_t, R_{t+1})\]

\(s\) 函数的具体形式将取决于效用函数 \(u\) 的选择。

\(w_t\) 和 \(R_{t+1}\) 共同代表经济中的价格（劳动力价格和资本租赁率）。

因此，(26.5) 表示给定价格下的储蓄量。

26.3.2. 示例：对数偏好

在特殊情况 \(u(c) = \log c\) 下，欧拉方程简化为 \(s_t= \beta (w_t - s_t)\)。

求解储蓄，我们得到

(26.6)\[ s_t = s(w_t, R_{t+1}) = \frac{\beta}{1+\beta} w_t\]

在这种特殊情况下，储蓄完全不受利率影响。

26.3.3. 储蓄与投资的关系

由于我们将人口规模标准化为1，\(s_t\)不仅代表个人储蓄，也代表了\(t\)时期整个经济的总储蓄。

在我们考虑的封闭经济模型中，不存在国际资本流动，因此国内净储蓄必然等于总投资，这构成了企业的资本供给。

接下来，我们将转向分析资本需求。

当我们将资本供给与需求相匹配时，就能确定OLG经济中的均衡状态。

26.4. 资本需求分析

下面我们先详细描述企业的最优化问题，然后推导出一个方程，用于表示在给定价格条件下的资本需求。

26.4.1. 企业问题

对于每个整数 \(t \geq 0\)，t期的产出 \(y_t\) 由**柯布-道格拉斯生产函数**给出

(26.7)\[ y_t = k_t^{\alpha} \ell_t^{1-\alpha}\]

在这里，\(k_t\) 表示资本投入，\(\ell_t\) 表示劳动投入，而 \(\alpha\) 是一个介于0和1之间的参数，通常被解释为”资本的产出弹性”。 企业面临的利润最大化问题是

(26.8)\[ \max_{k_t, \ell_t} \{ k^{\alpha}_t \ell_t^{1-\alpha} - R_t k_t -w_t \ell_t \}\]

一阶条件是通过对资本和劳动分别求导，并令导数等于零得到的：

\[ (1-\alpha)(k_t / \ell_t)^{\alpha} = w_t \quad \text{and} \quad \alpha (k_t / \ell_t)^{\alpha - 1} = R_t\]

26.4.2. 需求

根据我们的假设\(\ell_t = 1\)，我们可以得到

(26.9)\[ w_t = (1-\alpha)k_t^\alpha \]

并且

(26.10)\[ R_t = \alpha k_t^{\alpha - 1} \]

重新整理 (26.10) 得出在时间 \(t+1\) 的总资本需求

(26.11)\[ k^d (R_{t+1}) := \left (\frac{\alpha}{R_{t+1}} \right )^{1/(1-\alpha)}\]

在Python中

def capital_demand(R, α):
    return (α/R)**(1/(1-α)) 

def capital_supply(R, β, w):
    R = np.ones_like(R)
    return R * (β / (1 + β)) * w

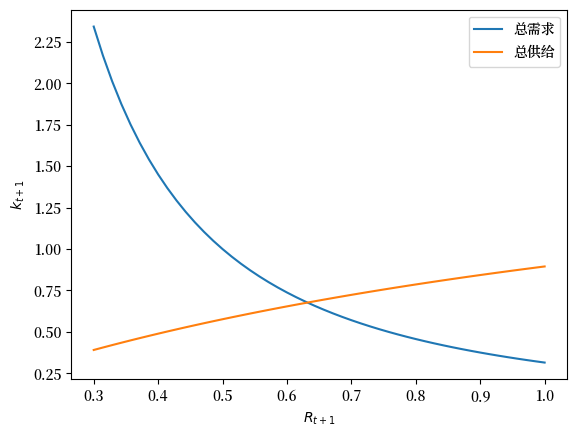
下图绘制了资本供给曲线（如(26.6)所示）以及资本需求曲线（如(26.11)所示），这两条曲线都是利率\(R_{t+1}\)的函数。 （对于对数效用这一特殊情况，供给不依赖于利率，因此我们得到一个常数函数。）

26.5. 均衡

在本节中，我们将推导均衡条件并研究一个例子。

26.5.1. 均衡条件

在均衡状态下，\(t\)时刻的储蓄等于\(t\)时刻的投资，也等于\(t+1\)时刻的资本供给。

通过将这些数量设为相等来计算均衡，即

(26.12)\[ s(w_t, R_{t+1}) = k^d(R_{t+1}) = \left (\frac{\alpha}{R_{t+1}} \right )^{1/(1-\alpha)}\]

原则上，我们现在可以给定\(w_t\)来求解均衡价格\(R_{t+1}\)。 （实际上，我们首先需要指定函数\(u\)，从而得到\(s\)。）

当我们求解这个关于\(t+1\)时刻结果的方程时，\(t\)时刻的量已经确定，所以我们可以将\(w_t\)视为常数。

从均衡\(R_{t+1}\)和(26.11)，我们可以得到 均衡数量\(k_{t+1}\)。

26.5.2. 示例：对数效用

在对数效用的情况下，我们可以使用(26.12)和(26.6)得到

(26.13)\[ \frac{\beta}{1+\beta} w_t = \left( \frac{\alpha}{R_{t+1}} \right)^{1/(1-\alpha)}\]

求解均衡利率得到

(26.14)\[ R_{t+1} = \alpha \left( \frac{\beta}{1+\beta} w_t \right)^{\alpha-1}\]

在Python中，我们可以通过以下方式计算这个

def equilibrium_R_log_utility(α, β, w):
    R = α * ( (β * w) / (1 + β))**(α - 1)
    return R

在对数效用的情况下，由于资本供给不依赖于利率，均衡数量是由供给固定的。

也就是说，

(26.15)\[ k_{t+1} = s(w_t, R_{t+1}) = \frac{\beta }{1+\beta} w_t\]

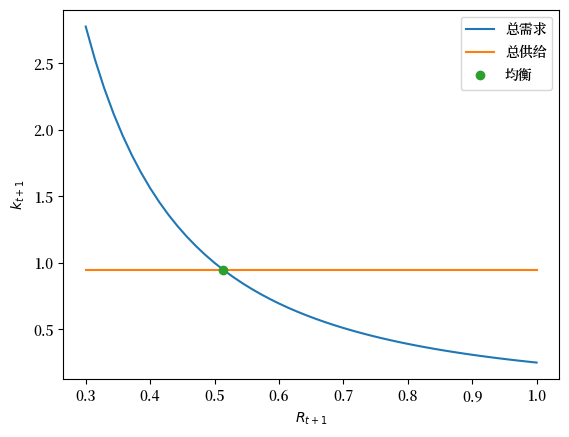
我们重新绘制上面的图，但这次加入均衡数量和价格。

R_vals = np.linspace(0.3, 1)
α, β = 0.5, 0.9
w = 2.0

fig, ax = plt.subplots()

ax.plot(R_vals, capital_demand(R_vals, α), 
        label="总需求")
ax.plot(R_vals, capital_supply(R_vals, β, w), 
        label="总供给")

R_e = equilibrium_R_log_utility(α, β, w)
k_e = (β / (1 + β)) * w

ax.plot(R_e, k_e, 'o',label='均衡')

ax.set_xlabel("$R_{t+1}$")
ax.set_ylabel("$k_{t+1}$")
ax.legend()
plt.show()

26.6. 动态分析

在本节中，我们将研究模型的动态行为。

我们主要关注对数效用的情况，此时均衡由方程(26.15)确定。

26.6.1. 资本积累过程

前面我们已经分析了如何根据当期工资\(w_t\)确定下一期的均衡资本\(k_{t+1}\)。

现在，我们可以利用(26.9)中的工资决定方程，将资本积累表示为一个关于当期资本\(k_t\)的函数。

具体来说，由于工资由\(w_t = (1-\alpha)k_t^\alpha\)给出，我们可以得到资本的演化方程

(26.16)\[ k_{t+1} = \frac{\beta}{1+\beta} (1-\alpha)(k_t)^{\alpha}\]

如果我们对这个方程进行迭代，我们将得到一个资本存量序列。

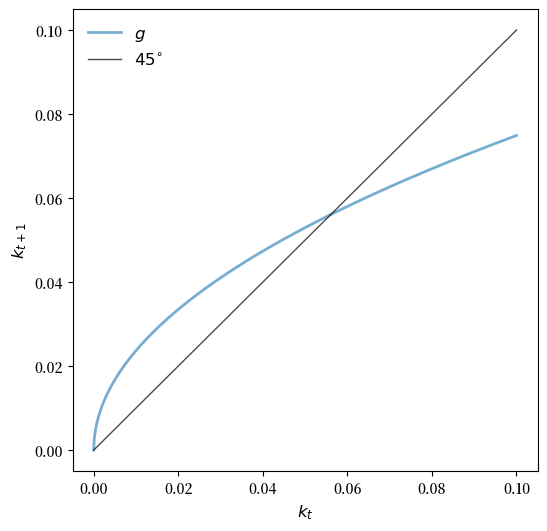
让我们绘制这些动态的45度图，我们将其表示为

\[ k_{t+1} = g(k_t) \quad \text{其中 } g(k) := \frac{\beta}{1+\beta} (1-\alpha)(k)^{\alpha} \]

def k_update(k, α, β):
    return β * (1 - α) * k**α /  (1 + β)

α, β = 0.5, 0.9
kmin, kmax = 0, 0.1
n = 1000
k_grid = np.linspace(kmin, kmax, n)
k_grid_next = k_update(k_grid,α,β)

fig, ax = plt.subplots(figsize=(6, 6))

ymin, ymax = np.min(k_grid_next), np.max(k_grid_next)

ax.plot(k_grid, k_grid_next,  lw=2, alpha=0.6, label='$g$')
ax.plot(k_grid, k_grid, 'k-', lw=1, alpha=0.7, label=r'$45^{\circ}$')


ax.legend(loc='upper left', frameon=False, fontsize=12)
ax.set_xlabel('$k_t$', fontsize=12)
ax.set_ylabel('$k_{t+1}$', fontsize=12)

plt.show()

26.6.2. 稳态（对数情况）

图表显示，该模型具有唯一的正稳态，我们将其表示为\(k^*\)。

我们可以通过设置\(k^* = g(k^*)\)来求解\(k^*\)，即

(26.17)\[ k^* = \frac{\beta (1-\alpha) (k^*)^{\alpha}}{(1+\beta)}\]

求解方程得到

(26.18)\[ k^* = \left (\frac{\beta (1-\alpha)}{1+\beta} \right )^{1/(1-\alpha)}\]

我们可以从(26.10)得到稳态利率，即

\[ R^* = \alpha (k^*)^{\alpha - 1} = \frac{\alpha}{1 - \alpha} \frac{1 + \beta}{\beta} \]

在Python中，我们有

k_star = ((β * (1 - α))/(1 + β))**(1/(1-α))
R_star = (α/(1 - α)) * ((1 + β) / β)

26.6.3. 时间序列

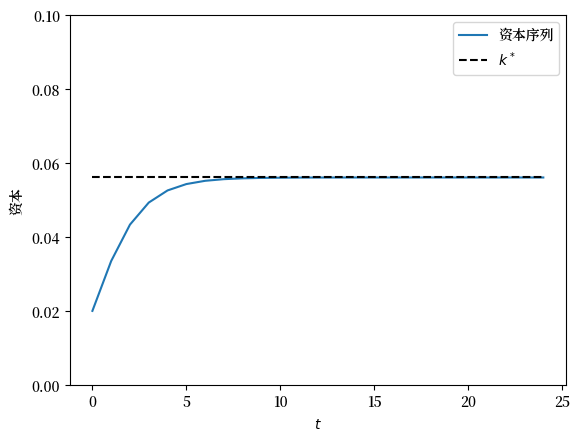
上面的45度图显示，具有正初始条件的资本时间序列会收敛到这个稳态。

让我们绘制一些时间序列来可视化这一点。

ts_length = 25
k_series = np.empty(ts_length)
k_series[0] = 0.02
for t in range(ts_length - 1):
    k_series[t+1] = k_update(k_series[t], α, β)

fig, ax = plt.subplots()
ax.plot(k_series, label="资本序列")
ax.plot(range(ts_length), np.full(ts_length, k_star), 'k--', label="$k^*$")
ax.set_ylim(0, 0.1)
ax.set_ylabel("资本")
ax.set_xlabel("$t$")
ax.legend()
plt.show()

如果你尝试不同的正初始值，你会发现这个序列总是收敛于\(k^*\)。

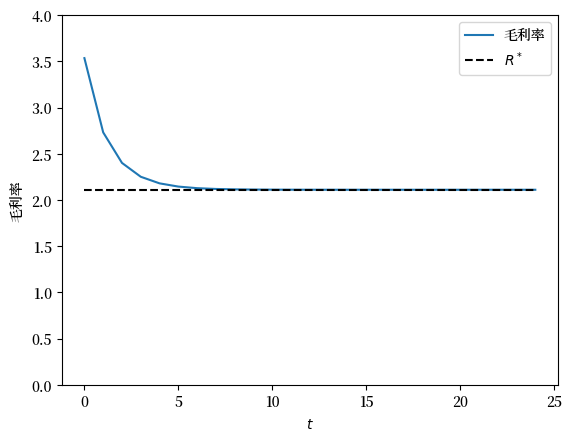
下面我们还绘制了随时间变化的总利率。

R_series = α * k_series**(α - 1)

fig, ax = plt.subplots()
ax.plot(R_series, label="毛利率")
ax.plot(range(ts_length), np.full(ts_length, R_star), 'k--', label="$R^*$")
ax.set_ylim(0, 4)
ax.set_ylabel("毛利率")
ax.set_xlabel("$t$")
ax.legend()
plt.show()

利率反映了资本的边际产出，当资本存量较低时，利率较高。

26.7. CRRA偏好

到目前为止，我们一直使用对数效用函数来分析模型。现在让我们扩展到更一般的情况。

对数效用实际上是常相对风险厌恶(CRRA)效用函数的一个特例，当风险厌恶参数\(\gamma\)趋近于1时得到。

在本节中，我们假设\(u(c) = \frac{ c^{1-\gamma}-1}{1-\gamma}\)，其中\(\gamma >0, \gamma\neq 1\)。

这个函数被称为CRRA效用函数。

在这一节中，我们将采用这种更一般的效用函数，同时保持模型的其他方面不变。

首先，让我们在Python中实现CRRA效用函数，并创建一个包含所有模型参数的数据结构。

def crra(c, γ):
    return c**(1 - γ) / (1 - γ)

Model = namedtuple('Model', ['α',        # 柯布-道格拉斯参数
                             'β',        # 折现因子
                             'γ']        # CRRA效用函数中的参数
                   )

def create_olg_model(α=0.4, β=0.9, γ=0.5):
    return Model(α=α, β=β, γ=γ)

让我们也重新定义资本需求函数，使其能够与这个namedtuple一起工作。

def capital_demand(R, model):
    return (α/R)**(1/(1-model.α)) 

26.7.1. 供给

对于家庭来说，欧拉方程变为

(26.19)\[ (w_t - s_t)^{-\gamma} = \beta R^{1-\gamma}_{t+1} (s_t)^{-\gamma}\]

求解储蓄，我们得到

(26.20)\[ s_t = s(w_t, R_{t+1}) = w_t \left [ 1 + \beta^{-1/\gamma} R_{t+1}^{(\gamma-1)/\gamma} \right ]^{-1}\]

请注意，与对数情况不同，储蓄现在取决于利率。

def savings_crra(w, R, model):
    α, β, γ = model
    return w / (1 + β**(-1/γ) * R**((γ-1)/γ)) 

model = create_olg_model()
w = 2.0

fig, ax = plt.subplots()

ax.plot(R_vals, capital_demand(R_vals, model), 
        label="总需求")
ax.plot(R_vals, savings_crra(w, R_vals, model), 
        label="总供给")

ax.set_xlabel("$R_{t+1}$")
ax.set_ylabel("$k_{t+1}$")
ax.legend()
plt.show()

26.7.2. 均衡

将资本的总需求（参见(26.11)）与我们新的总供给函数相等，即可得出均衡资本。

因此，我们设定

(26.21)\[ w_t \left [ 1 + \beta^{-1/\gamma} R_{t+1}^{(\gamma-1)/\gamma} \right ]^{-1} = \left (\frac{R_{t+1}}{\alpha} \right )^{1/(\alpha - 1)}\]

这个表达式相当复杂，我们无法解析地求解 \(R_{t+1}\)。

将(26.10)和(26.21)结合起来，得到

(26.22)\[ k_{t+1} = \left [ 1 + \beta^{-1/\gamma} (\alpha k^{\alpha - 1}_{t+1})^{(\gamma-1)/\gamma} \right ]^{-1} (1-\alpha)(k_t)^{\alpha}\]

同样，有了这个等式和给定的 \(k_t\)，我们无法用纸笔求解 \(k_{t+1}\)。

在下面的练习中，你将被要求用数值方法解这些方程。

26.8. 练习

Exercise 26.1

使用(26.22)在 CRRA 情况下数值求解均衡资本存量的动态。

使用 45 度图来可视化这个动态过程。

Solution to Exercise 26.1

为了在给定 \(k_t\) 的情况下求解 \(k_{t+1}\)，我们使用牛顿法。

设

(26.23)\[ f(k_{t+1}, k_t) = k_{t+1} \left[ 1 + \beta^{-1/\gamma} \left ( \alpha k^{\alpha-1}_{t+1} \right )^{(\gamma-1)/\gamma} \right] - (1-\alpha) k^{\alpha}_t =0\]

如果给定了 \(k_t\)，那么 \(f\) 就是未知数 \(k_{t+1}\) 的函数。

然后我们可以使用 scipy.optimize.newton 求解 \(f(k_{t+1}, k_t)=0\) 来得到 \(k_{t+1}\)。

首先让我们定义 \(f\)。

def f(k_prime, k, model):
    α, β, γ = model.α, model.β, model.γ
    z = (1 - α) * k**α
    a = α**(1-1/γ)
    b = k_prime**((α * γ - α + 1) / γ)
    p = k_prime + k_prime * β**(-1/γ) * a * b
    return p - z

现在让我们定义一个函数来找出 \(k_{t+1}\) 的值。

def k_update(k, model):
    return optimize.newton(lambda k_prime: f(k_prime, k, model), 0.1)

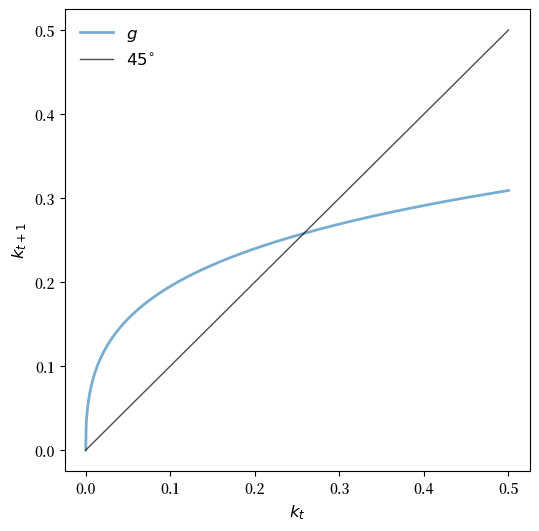
最后，这是 45 度图。

kmin, kmax = 0, 0.5
n = 1000
k_grid = np.linspace(kmin, kmax, n)
k_grid_next = np.empty_like(k_grid)

for i in range(n):
    k_grid_next[i] = k_update(k_grid[i], model)

fig, ax = plt.subplots(figsize=(6, 6))

ymin, ymax = np.min(k_grid_next), np.max(k_grid_next)

ax.plot(k_grid, k_grid_next,  lw=2, alpha=0.6, label='$g$')
ax.plot(k_grid, k_grid, 'k-', lw=1, alpha=0.7, label=r'$45^{\circ}$')


ax.legend(loc='upper left', frameon=False, fontsize=12)
ax.set_xlabel('$k_t$', fontsize=12)
ax.set_ylabel('$k_{t+1}$', fontsize=12)

plt.show()

Exercise 26.2

上一个练习中的45度图表明存在唯一的正稳态。

通过在(26.22)中设置 \(k_{t+1} = k_t = k^*\)，可以得到正稳态，即：

\[ k^* = \frac{(1-\alpha)(k^*)^{\alpha}} {1 + \beta^{-1/\gamma} (\alpha (k^*)^{\alpha-1})^{(\gamma-1)/\gamma}} \]

与对数效用情况不同，CRRA效用的稳态 \(k^*\) 无法通过解析方法获得。

相反，我们使用牛顿法求解 \(k^*\)。

Solution to Exercise 26.2

我们引入一个函数 \(h\)，使得 正稳态是 \(h\) 的根。

(26.24)\[ h(k^*) = k^* \left [ 1 + \beta^{-1/\gamma} (\alpha (k^*)^{\alpha-1})^{(\gamma-1)/\gamma} \right ] - (1-\alpha)(k^*)^{\alpha}\]

现在让我们用Python实现这个函数：

def h(k_star, model):
    α, β, γ = model.α, model.β, model.γ
    z = (1 - α) * k_star**α
    R1 = α ** (1-1/γ)
    R2 = k_star**((α * γ - α + 1) / γ)
    p = k_star + k_star * β**(-1/γ) * R1 * R2
    return p - z

让我们运用牛顿法来求根：

k_star = optimize.newton(h, 0.2, args=(model,))
print(f"k_star = {k_star}")

k_star = 0.25788950250843484

Exercise 26.3

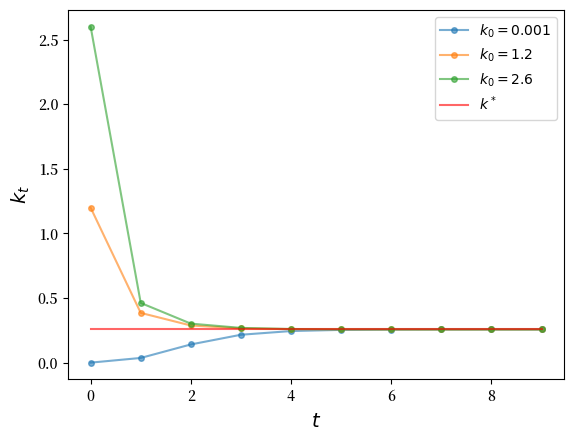
根据上面列出的参数化，生成三个资本的时间路径，来自三个不同的初始条件。

使用 \(k_0\) 的初始条件为 \(0.001, 1.2, 2.6\)，并且时间序列长度为 10。

Solution to Exercise 26.3

让我们定义常数和三个不同的初始条件。

ts_length = 10
k0 = np.array([0.001, 1.2, 2.6])

现在我们定义一个函数来模拟时间序列。

def simulate_ts(model, k0_values, ts_length):

    fig, ax = plt.subplots()

    ts = np.zeros(ts_length)

    # 模拟并且绘制时间序列
    for k_init in k0_values:
        ts[0] = k_init
        for t in range(1, ts_length):
            ts[t] = k_update(ts[t-1], model)
        ax.plot(np.arange(ts_length), ts, '-o', ms=4, alpha=0.6,
                label=r'$k_0=%g$' %k_init)
    ax.plot(np.arange(ts_length), np.full(ts_length, k_star),
            alpha=0.6, color='red', label=r'$k^*$')
    ax.legend(fontsize=10)

    ax.set_xlabel(r'$t$', fontsize=14)
    ax.set_ylabel(r'$k_t$', fontsize=14)

    plt.show()

现在我们可以模拟时间序列并绘制结果。

simulate_ts(model, k0, ts_length)