30. 通货膨胀税的拉弗曲线#

30.1. 概述#

本讲座研究了通货膨胀税的静态和动态拉弗曲线，使用的是讲座通过货币资助的政府赤字和价格水平中研究的模型的非线性模型版本。

我们采用了[Cagan, 1956]在其经典论文中使用的对数线性货币需求函数，而不是讲座通过货币资助的政府赤字和价格水平中使用的线性需求函数。

这一改变需要我们修改部分分析。

特别是,我们的动态系统在状态变量上不再是线性的。

然而,基于我们所谓的”方法2”的经济逻辑分析仍然保持不变。

我们将发现与讲座通过货币资助的政府赤字和价格水平中研究的结果类似的定性结果。

该讲座展示了本讲座中模型的线性版本。

与那个讲座一样,我们讨论以下主题:

政府通过印制纸币或电子货币征收的通货膨胀税
通货膨胀税率中存在两个静态均衡的动态拉弗曲线
在理性预期下的反常动态,系统趋向于较高的静态通货膨胀税率
与该静态通货膨胀率相关的奇特的比较静态分析,它表明通货膨胀可以通过运行更高的政府赤字来降低

这些结果为分析拉弗曲线与自适应预期做准备,该讲座在使用”适应性预期”而不是理性预期下研究了这个模型。

该讲座将展示:

用适应性预期替代理性预期不改变两个静态通货膨胀率,但是 $\dots$
它通过使系统通常收敛于较低的静态通货膨胀率来逆转反常动态
现在通货膨胀可以通过运行较低的政府赤字来降低,从而出现了更合理的比较动态结果

30.2. 模型#

设:

$m_{t}$ 为时间 $t$ 初的货币供应量对数
$p_{t}$ 为时间 $t$ 的价格水平对数

货币需求函数为:

(30.1)#

m_{t + 1} - p_{t} = - α (p_{t + 1} - p_{t})

其中 $α \geq 0$ 。

货币供应量的动态方程为:

(30.2)#

\exp (m_{t + 1}) - \exp (m_{t}) = g \exp (p_{t})

其中 $g$ 是政府支出中通过印钞来融资的部分。

注意: 方程(30.1)在货币供应量和价格水平的对数上是线性的, 方程(30.2)在价格水平上是线性的。这需要我们调整在讲座通过货币资助的政府赤字和价格水平中使用的均衡计算方法。

30.3. 通货膨胀率的极限#

我们可以通过研究稳态拉弗曲线来计算 $\overset{―}{π}$ 的两个可能极限值。

因此,在稳态中

m_{t + 1} - m_{t} = p_{t + 1} - p_{t} = x \forall t,

其中 $x > 0$ 是货币供应量和价格水平的对数的共同增长率。

几行代数运算可以得出 $x$ 满足的方程:

(30.3)#

\exp (- α x) - \exp (- (1 + α) x) = g

我们需要

(30.4)#

g \leq max_{x \geq 0} {\exp (- α x) - \exp (- (1 + α) x)},

这样通过印钞来融资才是可行的。

(30.3)的左侧是通过印钞筹集的稳态收入。

(30.3)的右侧是政府在时间 $t$ 通过印钞筹集的商品数量。

稍后我们将绘制方程(30.3)的左右两侧。

但首先让我们编写代码来计算稳态 $\overset{―}{π}$ 。

让我们先导入一些库

from collections import namedtuple
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from scipy.optimize import fsolve 

FONTPATH = "fonts/SourceHanSerifSC-SemiBold.otf"
mpl.font_manager.fontManager.addfont(FONTPATH)
plt.rcParams['font.family'] = ['Source Han Serif SC']

让我们创建一个namedtuple来存储模型的参数

CaganLaffer = namedtuple('CaganLaffer', 
                        ["m0",  # t=0时货币供应量的对数
                         "α",   # 货币需求的灵敏度
                         "λ",
                         "g" ])

# 创建一个 凯根拉弗 模型 
def create_model(α=0.5, m0=np.log(100), g=0.35):
    return CaganLaffer(α=α, m0=m0, λ=α/(1+α), g=g)

model = create_model()

现在我们编写计算稳态 $\overset{―}{π}$ 的代码。

# 定义π_bar的公式
def solve_π(x, α, g):
    return np.exp(-α * x) - np.exp(-(1 + α) * x) - g

def solve_π_bar(model, x0):
    π_bar = fsolve(solve_π, x0=x0, xtol=1e-10, args=(model.α, model.g))[0]
    return π_bar

# 求解两个稳态的π
π_l = solve_π_bar(model, x0=0.6)
π_u = solve_π_bar(model, x0=3.0)
print(f'两个稳态的π是: {π_l, π_u}')

两个稳态的π是: (0.6737147075333032, 1.6930797322614812)

我们找到两个稳态 $\overset{―}{π}$ 的值。

30.4. 稳态拉弗曲线#

以下图形展示了稳态拉弗曲线以及两个稳态通货膨胀率。

def compute_seign(x, α):
    return np.exp(-α * x) - np.exp(-(1 + α) * x)

def plot_laffer(model, πs):
    α, g = model.α, model.g
    
    # 生成 π 值
    x_values = np.linspace(0, 5, 1000)

    # 计算对应的铸币税值
    y_values = compute_seign(x_values, α)

    # 绘制函数
    plt.plot(x_values, y_values, 
            label=f'拉弗曲线')
    for π, label in zip(πs, [r'$\pi_l$', r'$\pi_u$']):
        plt.text(π, plt.gca().get_ylim()[0]*2, 
                 label, horizontalalignment='center',
                 color='brown', size=10)
        plt.axvline(π, color='brown', linestyle='--')
    plt.axhline(g, color='red', linewidth=0.5, 
                linestyle='--', label='g')
    plt.xlabel(r'$\pi$')
    plt.ylabel('铸币税')
    plt.legend()
    plt.show()

# 稳态拉弗曲线
plot_laffer(model, (π_l, π_u))

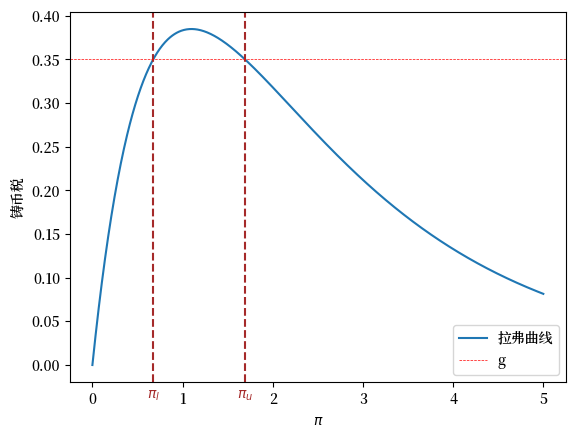
_images/b86626feedc8af4e855ef9d74c4ccf1ce437639c240994d1ad892fa2a97caf6b.png — Fig. 30.1 稳态通胀的铸币税功能。棕色虚线代表 $π_{l}$ 和 $π_{u}$ 。#

30.5. 初始价格水平的计算#

现在我们已经掌握了两个可能的稳态，我们可以计算两个函数 $\underset{―}{p} (m_{0})$ 和 $\overset{―}{p} (m_{0})$ ，作为时间 $t$ 时 $p_{t}$ 的初始条件。这意味着我们需要找到对于所有 $t \geq 0$ ， $π_{t} = \overset{―}{π}$ 。

函数 $\underset{―}{p} (m_{0})$ 将会与较低的稳态通货膨胀率 $π_{l}$ 相关联。

函数 $\overset{―}{p} (m_{0})$ 将会与较高的稳态通货膨胀率 $π_{u}$ 相关联。

def solve_p0(p0, m0, α, g, π):
    return np.log(np.exp(m0) + g * np.exp(p0)) + α * π - p0

def solve_p0_bar(model, x0, π_bar):
    p0_bar = fsolve(solve_p0, x0=x0, xtol=1e-20, args=(model.m0, 
                                                       model.α, 
                                                       model.g, 
                                                       π_bar))[0]
    return p0_bar

# 计算与 π_l 和 π_u 关联的两个初始价格水平
p0_l = solve_p0_bar(model, 
                    x0=np.log(220), 
                    π_bar=π_l)
p0_u = solve_p0_bar(model, 
                    x0=np.log(220), 
                    π_bar=π_u)
print(f'关联的初始 p_0s 是: {p0_l, p0_u}')

关联的初始 p_0s 是: (5.615742247288047, 7.144789784380314)

30.5.1. 验证#

首先，让我们编写一些代码来验证，如果初始对数价格水平 $p_{0}$ 取我们刚刚计算的两个值之一，那么通货膨胀率 $π_{t}$ 将对所有的 $t \geq 0$ 保持恒定。

下面的代码进行了验证。

def simulate_seq(p0, model, num_steps):
    λ, g = model.λ, model.g
    π_seq, μ_seq, m_seq, p_seq = [], [], [model.m0], [p0]

    for t in range(num_steps):
        
        m_seq.append(np.log(np.exp(m_seq[t]) + g * np.exp(p_seq[t])))
        p_seq.append(1/λ * p_seq[t] + (1 - 1/λ) * m_seq[t+1])

        μ_seq.append(m_seq[t+1]-m_seq[t])
        π_seq.append(p_seq[t+1]-p_seq[t])

    return π_seq, μ_seq, m_seq, p_seq

π_seq, μ_seq, m_seq, p_seq = simulate_seq(p0_l, model, 150)

# 在稳态下检查 π 和 μ
print('π_bar == μ_bar:', π_seq[-1] == μ_seq[-1])

# 检查稳态下的 m_{t+1} - m_t 和 p_{t+1} - p_t
print('m_{t+1} - m_t:', m_seq[-1] - m_seq[-2])
print('p_{t+1} - p_t:', p_seq[-1] - p_seq[-2])

# 检验 exp(-αx) - exp(-(1 + α)x) = g
eq_g = lambda x: np.exp(-model.α * x) - np.exp(-(1 + model.α) * x)

print('eq_g == g:', np.isclose(eq_g(m_seq[-1] - m_seq[-2]), model.g))

π_bar == μ_bar: True
m_{t+1} - m_t: 1.693079732261424
p_{t+1} - p_t: 1.693079732261424
eq_g == g: True

30.6. 计算均衡序列#

我们将采用类似于通过货币资助的政府赤字和价格水平中的 方法2。

我们将时间 $t$ 的状态向量视为对 $(m_{t}, p_{t})$ 。

我们将 $m_{t}$ 视为一个 自然状态变量，而 $p_{t}$ 视为一个跳跃变量。

定义

λ \equiv \frac{α}{1 + α}

让我们重写方程 (30.1) 为

(30.5)#

p_{t} = (1 - λ) m_{t + 1} + λ p_{t + 1}

让我们用伪代码来描述计算均衡序列的算法。

伪代码

算法的核心是从一个时期到下一个时期的状态转移。在每个时期 $t$ ，我们有:

状态变量: $(m_{t}, p_{t})$ ，其中
- $m_{t}$ 是货币供应量的对数
- $p_{t}$ 是价格水平的对数
状态转移步骤:
- 根据 (30.2) 计算下一期货币供应量 $m_{t + 1}$
- 根据 (30.5) 计算下一期价格水平 $p_{t + 1} = λ^{- 1} p_{t} + (1 - λ^{- 1}) m_{t + 1}$
- 计算通货膨胀率 $π_{t} = p_{t + 1} - p_{t}$ 和货币增长率 $μ_{t} = m_{t + 1} - m_{t}$

要运行完整的模拟:

选择初始条件:
- 设定初始货币供应量 $m_{0} > 0$
- 在区间 $[\underset{―}{p} (m_{0}), \overset{―}{p} (m_{0})]$ 中选择初始价格水平 $p_{0}$
重复执行状态转移步骤，直到通货膨胀率 $π_{t}$ 和货币增长率 $μ_{t}$ 收敛到它们的稳态值 $\overset{―}{π}$ 和 $\overset{―}{μ}$

结果将表明：

如果它们存在，极限值 $\overset{―}{π}$ 和 $\overset{―}{μ}$ 将是相等的
如果极限值存在，有两个可能的极限值，一个高，一个低
对于几乎所有初始对数价格水平 $p_{0}$ ，极限 $\overset{―}{π} = \overset{―}{μ}$ 是更高的值
对于两个可能的极限值 $\overset{―}{π}$ 中的每一个，存在一个独特的初始对数价格水平 $p_{0}$ ，它意味着所有 $t \geq 0$ 的 $π_{t} = μ_{t} = \overset{―}{μ}$
- 这个独特的初始对数价格水平解决了 $\log (\exp (m_{0}) + g \exp (p_{0})) - p_{0} = - α \overset{―}{π}$
- 上述关于 $p_{0}$ 的方程源自 $m_{1} - p_{0} = - α \overset{―}{π}$

30.7. 拉弗曲线动态的不稳定性#

与通过货币资助的政府赤字和价格水平和通货膨胀税的拉弗曲线类似，我们现在已经具备了从不同的 $p_{- 1}, π_{- 1}^{*}$ 开始计算时间序列的能力。

# 从 p0_l 到 p0_u 生成一个序列
p0s = np.arange(p0_l, p0_u, 0.1) 

line_params = {'lw': 1.5, 
              'marker': 'o',
              'markersize': 3}

p0_bars = (p0_l, p0_u)
              
draw_iterations(p0s, model, line_params, p0_bars, num_steps=20)

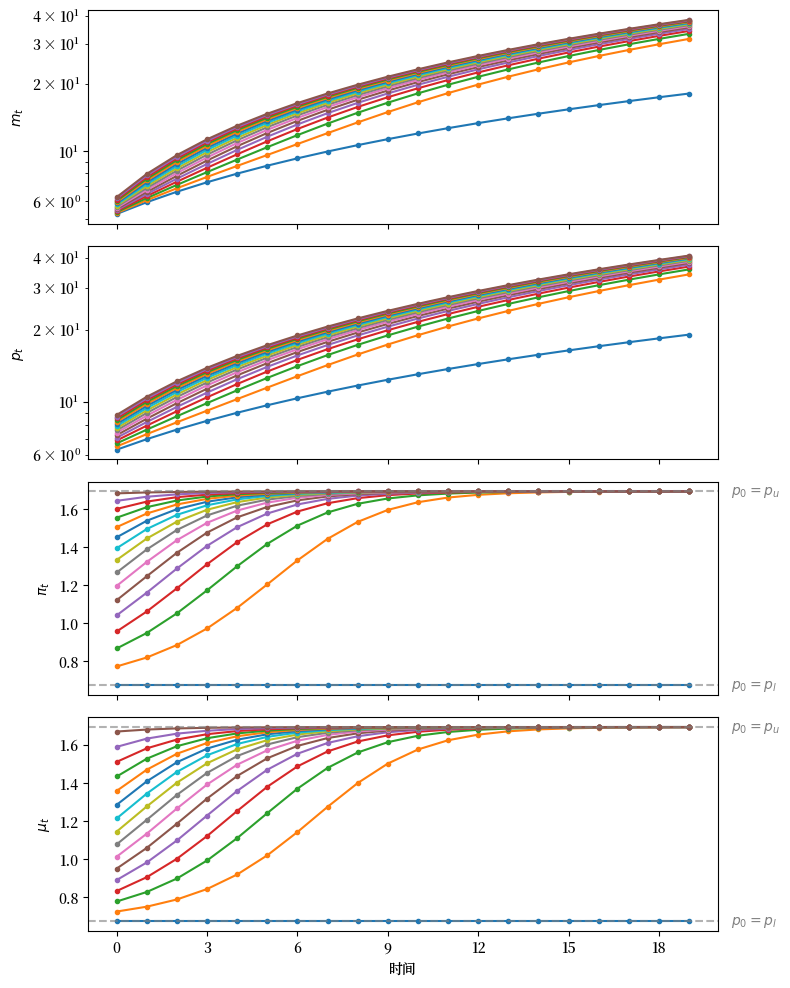
_images/6a4488908453055eef13cf0084f55d111e4197511afe70aacfe0ef8a4d0f0626.png — Fig. 30.2 从不同的初始值 $p_{0}$ 开始， $m_{t}$ （顶部面板， $m$ 使用对数刻度）， $p_{t}$ （第二面板， $p$ 使用对数刻度）， $π_{t}$ （第三面板）和 $μ_{t}$ （底部面板）的路径#

观察 Fig. 30.2 中的价格水平路径，我们发现几乎所有路径都收敛到固定状态拉弗曲线中的较高通货膨胀税率，如图 Fig. 30.1 所示。

这再次证实了我们所说的”反常”动态现象 - 在理性预期下，系统倾向于收敛到两个可能的固定通货膨胀税率中较高的那个。

这种动态被称为”反常”有两个原因。首先，它意味着货币和财政当局选择通过通货膨胀税来为政府支出融资。其次，从图 Fig. 30.1 中的固定状态拉弗曲线可以看出一个”违反直觉”的结果：

图表显示，通过运行更高的政府赤字，即通过增加印钞筹集更多资源，可以降低通货膨胀。

Note

在通过货币资助的政府赤字和价格水平中研究的模型的线性版本中也普遍存在同样的定性结果。

我们的分析表明：

除了一条独特的路径外，所有均衡路径都会收敛到较高的通货膨胀税率
这条独特的路径收敛到较低的通货膨胀税率，这与我们的直觉相符 - 即降低政府赤字应该降低通货膨胀率

正如在通过货币资助的政府赤字和价格水平中讨论的那样，从经济学的角度来看，选择收敛到较低通货膨胀率的均衡路径更为合理。

这个选择对于理解我们在一些不愉快的货币主义算术中将要探讨的”不愉快算术”结果至关重要。

在接下来的拉弗曲线与自适应预期中，我们会看到 [Bruno and Fischer, 1990] 等学者如何从不同角度论证这种均衡选择的合理性。